JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. Let C be the capacitance of a capacitor discharging through a resistor R. Suppose $t_{1}$ is the time taken for the energy stored in the capacitor to reduce to half its initial value and $t_{2}$ is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio $t_{1} / t_{2}$ will be
(1) 2
(2) 1
(3) 1/2
(4) 1/4
[AIEEE-2010]
Ans. (3)
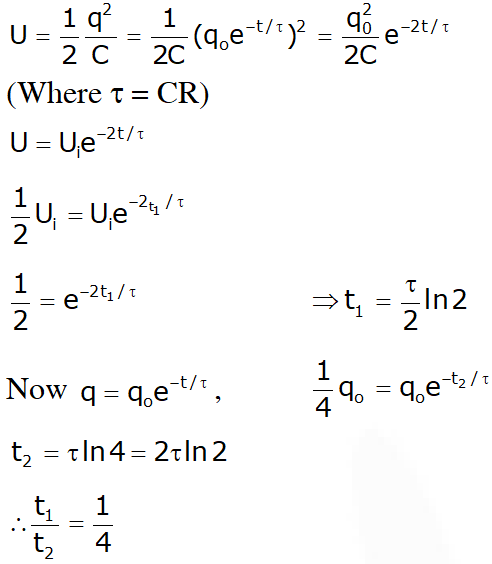
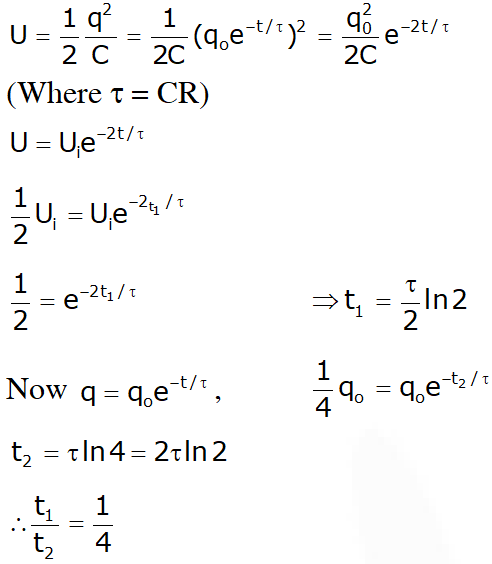
Q. Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30° with each other. When suspended in a liquid of density 0.8 g $\mathrm{cm}^{-3}$, the angle remains the same. If density of the material of the sphere is $1.6 \mathrm{g} \mathrm{cm}^{-3}$, the dielectric constant of the liquid is :
(1) 1
(2) 4
(3) 3
(4) 2
[AIEEE - 2010]
Ans. (4)
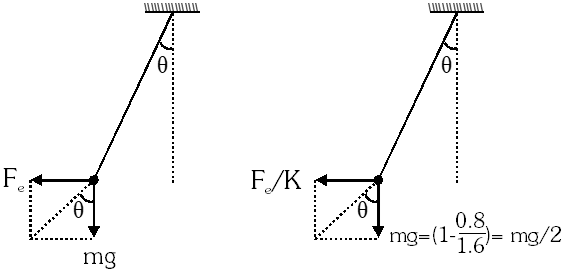Therefore K =2
Therefore K =2
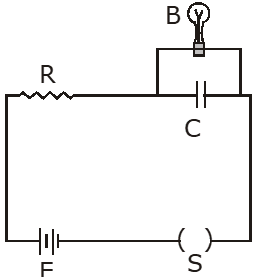
Q. A resistor 'R' and $2 \mu \mathrm{F}$ capacitor in series is connected through a switch to 200 V direct supply. Across the capacitor is a neon bulb that lights up at 120 V. Calculate the value of R to make the bulb light up 5s after the switch has been closed. ($\log _{10}$ 2.5 = 0.4)
(1) $2.7 \times 10^{6} \Omega$
(2) $3.3 \times 10^{7} \Omega$
(3) $1.3 \times 10^{4} \Omega$
(4) $1.7 \times 10^{5} \Omega$
[AIEEE-2011]
Ans. (2)
Neon bulb is filled with gas, so its resistance is infinite, hence no current flows through it.
Now, $\mathrm{V}_{\mathrm{c}}=\mathrm{E}\left(1-\mathrm{e}^{-\mathrm{t} / \mathrm{RC}}\right)$
$\Rightarrow 120=200\left(1-\mathrm{e}^{-\mathrm{t} / \mathrm{RC}}\right)$
$\Rightarrow \mathrm{e}^{-\mathrm{t} / \mathrm{RC}}=\frac{2}{5} \Rightarrow \mathrm{t}=\mathrm{RCln} 2.5$
$\Rightarrow \mathrm{R}=\frac{\mathrm{t}}{\mathrm{Cln} 2.5}=\frac{\mathrm{t}}{2.303 \mathrm{Clog} 2.5}$
$=2.7 \times 10^{6} \Omega$
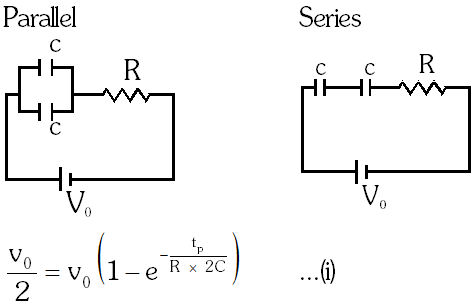
Q. Combination of two identical capacitors, a resistor R and a dc voltage source of voltage 6V is used in an experiment on (C–R) circuit. It is found that for a parallel combination of the capacitor the time in which the voltage of the fully charged combination reduces to half its original voltage is 10 second. For series combination the time needed for reducing the voltage of the fully charged series combination by half is :-
(1) 20 second
(2) 10 second
(3) 5 second
(4) 2.5 second
[AIEEE-2011]
Ans. (4)
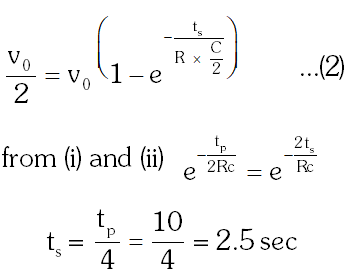
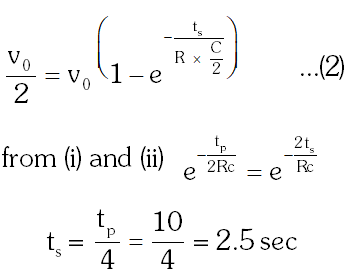
Q. The figure shows an experimental plot for discharging of a capacitor in an R–C circuit. The time constant t of this circuit lies between:-
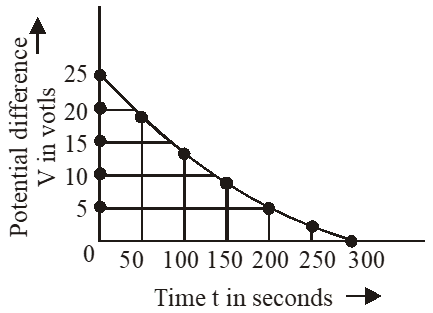(1) 100 sec and 150 sec
(2) 150 sec and 200 sec
(3) 0 and 50 sec
(4) 50 sec and 100 sec
[AIEEE-2012]
(1) 100 sec and 150 sec
(2) 150 sec and 200 sec
(3) 0 and 50 sec
(4) 50 sec and 100 sec
[AIEEE-2012]
Ans. (1)
$\mathrm{t}=0.37 \% \mathrm{of} \mathrm{V}_{0}$
$=0.37 \times 25=9.25$ volt
where is in between 100 and 150 sec.
Q. Two capacitors $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ are charged to 120V and 200V respectively. It is found that by connecting them together the potential on each one can be made zero. Then :
(1) $5 \mathrm{C}_{1}=3 \mathrm{C}_{2}$
(2) $3 \mathrm{C}_{1}=5 \mathrm{C}_{2}$
(3) $3 \mathrm{C}_{1}+5 \mathrm{C}_{2}=0$
(4) $9 \mathrm{C}_{1}=4 \mathrm{C}_{2}$
[JEE-Mains-2013]
Ans. (2)
Common voltage $=\frac{\mathrm{C}_{1} \mathrm{v}_{1}-\mathrm{C}_{2} \mathrm{V}_{2}}{\mathrm{C}_{1}+\mathrm{C}_{2}}$
(positive plate of one capacitor is connected with negative plate of second capacitor)
$\Rightarrow 120 \mathrm{C}_{1}=200 \mathrm{C}_{2} \Rightarrow 3 \mathrm{C}_{1}=5 \mathrm{C}_{2}$
Q. A parallel plate capacitor is made of two circular plates separated by a distance of 5 mm and with a dielectriic of dielectric constant 2.2 between them. When the electric field in the dielectric field in the dielectric is $3 \times 10^{4}$ V/m, the charge density of the positive plate will be close
to :
(1) $3 \times 10^{4} \mathrm{C} / \mathrm{m}^{2}$
(2) $6 \times 10^{4} \mathrm{C} / \mathrm{m}^{2}$
(3) $6 \times 10^{-7} \mathrm{C} / \mathrm{m}^{2}$
(4) $3 \times 10^{-7} \mathrm{C} / \mathrm{m}^{2}$
[JEE-Mains-2014]
Ans. (3)
$\frac{\sigma}{\mathrm{K} \varepsilon_{0}}=3 \times 10^{4}$
$\frac{\sigma}{2.25 \times 8.86 \times 10^{-12}}=3 \times 10^{4}$
$\sigma=6 \times 10^{-7} \mathrm{C} / \mathrm{m}^{2}$
Q. In the given circuit, charge $\mathrm{Q}_{2}$ on the 2µF capacitor changes as C is varied from $1 \mu \mathrm{F}$ to $3 \mu \mathrm{F} \cdot \mathrm{Q}_{2}$ as a function of 'C' is given properly by : (figures are drawn schematically and are not to scale) :-
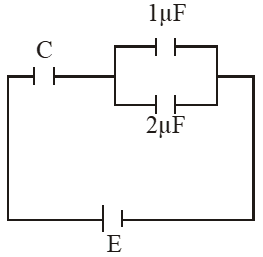
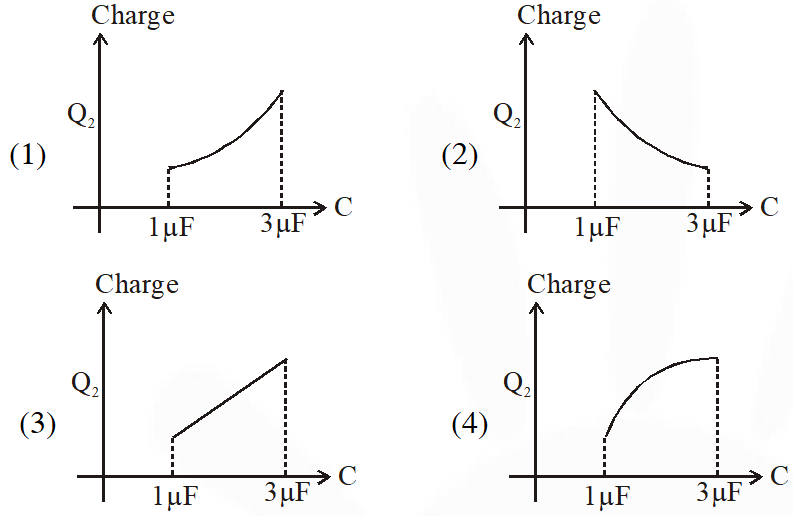[JEE-Mains-2015]
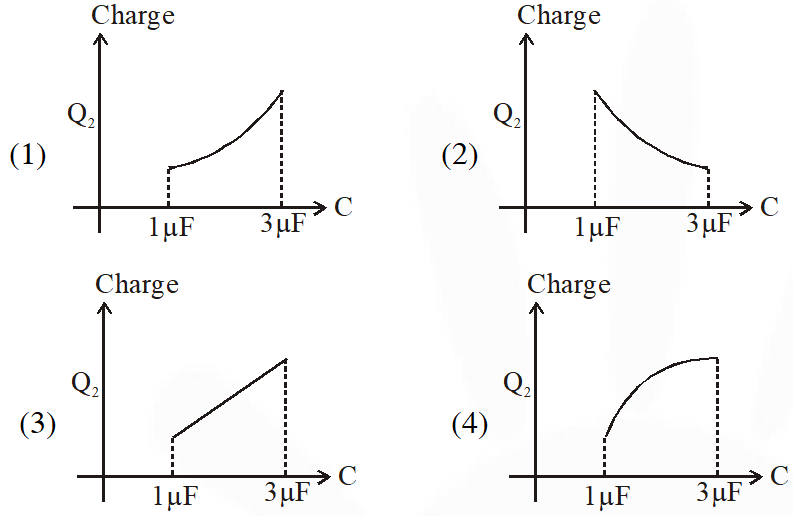[JEE-Mains-2015]
Ans. (4)
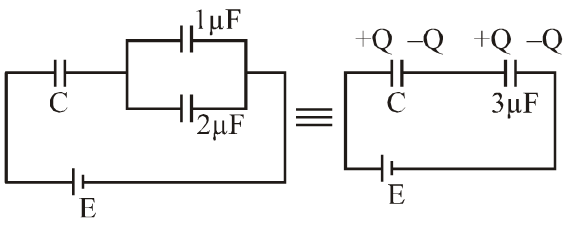$\mathrm{C}_{\mathrm{eq}}=\frac{3 \mathrm{C}}{3+\mathrm{C}} \quad \mathrm{Q}=\mathrm{Ceq} \mathrm{E}$
$\mathrm{Q}_{2}=\frac{2 \mathrm{CE}}{(\mathrm{C}+3)}=\frac{3 \mathrm{CE}}{(\mathrm{C}+3)}$
$=2 \mathrm{E}\left[1-\frac{3}{\mathrm{C}+3}\right]$
$\mathrm{Q}_{2 / \mathrm{when}} \mathrm{C}=1_{\mathrm{HF}}=2 \mathrm{E}\left[\frac{1}{4}\right]=\frac{\mathrm{E}}{2}$
$\mathrm{Q}_{2 / \mathrm{when}} \mathrm{C}=3_{1 \mathrm{F}}=2 \mathrm{E}\left[\frac{1}{2}\right]=\mathrm{E}$
$\frac{\mathrm{dQ}}{\mathrm{d} \mathrm{C}}=-\frac{2 \mathrm{E} \cdot 3}{(\mathrm{C}+3)}(-1)=\frac{6 \mathrm{E}}{(\mathrm{C}+3)^{2}}>0$
$\frac{\mathrm{d}^{2} \theta}{\mathrm{d} \mathrm{C}^{2}}=\frac{6 \mathrm{E}(-2)}{(\mathrm{C}+3)^{3}}=-\frac{12 \mathrm{E}}{(\mathrm{C}+3)^{2}}<0$
$\mathrm{C}_{\mathrm{eq}}=\frac{3 \mathrm{C}}{3+\mathrm{C}} \quad \mathrm{Q}=\mathrm{Ceq} \mathrm{E}$
$\mathrm{Q}_{2}=\frac{2 \mathrm{CE}}{(\mathrm{C}+3)}=\frac{3 \mathrm{CE}}{(\mathrm{C}+3)}$
$=2 \mathrm{E}\left[1-\frac{3}{\mathrm{C}+3}\right]$
$\mathrm{Q}_{2 / \mathrm{when}} \mathrm{C}=1_{\mathrm{HF}}=2 \mathrm{E}\left[\frac{1}{4}\right]=\frac{\mathrm{E}}{2}$
$\mathrm{Q}_{2 / \mathrm{when}} \mathrm{C}=3_{1 \mathrm{F}}=2 \mathrm{E}\left[\frac{1}{2}\right]=\mathrm{E}$
$\frac{\mathrm{dQ}}{\mathrm{d} \mathrm{C}}=-\frac{2 \mathrm{E} \cdot 3}{(\mathrm{C}+3)}(-1)=\frac{6 \mathrm{E}}{(\mathrm{C}+3)^{2}}>0$
$\frac{\mathrm{d}^{2} \theta}{\mathrm{d} \mathrm{C}^{2}}=\frac{6 \mathrm{E}(-2)}{(\mathrm{C}+3)^{3}}=-\frac{12 \mathrm{E}}{(\mathrm{C}+3)^{2}}<0$
Q. A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the $4 \mu \mathrm{F}$ and $9 \mu \mathrm{F}$capacitors), at a point 30 m from it , would equal:
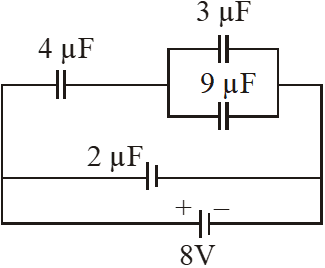(1) 480 N/C
(2) 240 N/C
(3) 360 N/C
(4) 420 N/C
[JEE-Mains-2016]
(1) 480 N/C
(2) 240 N/C
(3) 360 N/C
(4) 420 N/C
[JEE-Mains-2016]
Ans. (4)
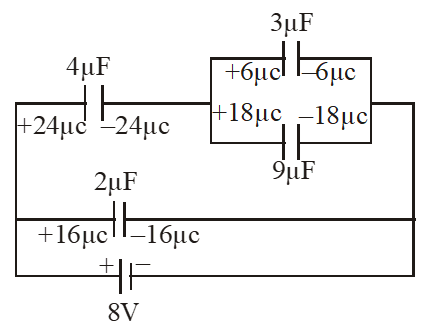$\mathrm{Q}=24+18=42 \mu \mathrm{c}$
$\mathrm{E}=\frac{\mathrm{KQ}}{\mathrm{r}^{2}}$
$\Rightarrow \mathrm{E}=\frac{9 \times 10^{9} \times 42 \times 10^{-6}}{(30)^{2}}=420 \mathrm{N} / \mathrm{C}$
$\mathrm{Q}=24+18=42 \mu \mathrm{c}$
$\mathrm{E}=\frac{\mathrm{KQ}}{\mathrm{r}^{2}}$
$\Rightarrow \mathrm{E}=\frac{9 \times 10^{9} \times 42 \times 10^{-6}}{(30)^{2}}=420 \mathrm{N} / \mathrm{C}$
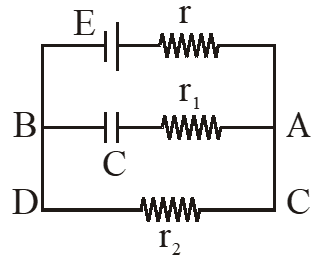
Q. In the given circuit diagram when the current reaches steady state in the circuit, the charge on the capacitor of capacitance C will be :
(1) $\mathrm{CE} \frac{\mathrm{r}_{2}}{\left(\mathrm{r}+\mathrm{r}_{2}\right)}$
(2) $\mathrm{CE} \frac{\mathrm{r}_{1}}{\left(\mathrm{r}_{1}+\mathrm{r}\right)}$
(3) CE
(4) $\mathrm{CE} \frac{\mathrm{r}_{1}}{\left(\mathrm{r}_{2}+\mathrm{r}\right)}$
[JEE-Mains-2017]
Ans. (1)
It steady state, current through AB = 0
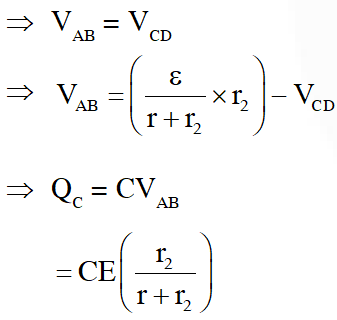
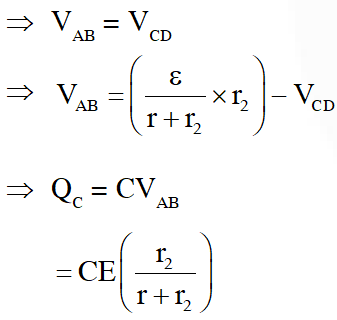
Q. A capacitance of 2 $\mu \mathrm{F}$ is required in an electrical circuit across a potential difference of 1.0 kV. A large number of 1 $\mu \mathrm{F}$ capacitors are available which can withstand a potential difference of not more than 300 V. The minimum number of capacitors required to achieve this is :
(1) 24
(2) 32
(3) 2
(4) 16
[JEE-Mains-2017]
Ans. (2)
To hold 1 KV potential differenceminimum four capacitors are required in series
$\Rightarrow \quad \mathrm{C}_{1}=\frac{1}{4}$ for one series. So for $\mathrm{Ceq}$ to be $2 \mu \mathrm{F}, 8$ parallel combinations are required.
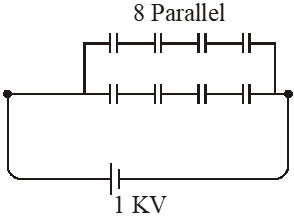$\Rightarrow$ Minimum no. of capacitors $=8 \times 4=32$
$\Rightarrow$ Minimum no. of capacitors $=8 \times 4=32$
Q. A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20V. If a dielectric material of dielectric constant $\mathrm{K}=\frac{5}{3}$ is inserted between the plates, the magnitude of the induced charge will be :-
(1) 0.3 n C
(2) 2.4 n C
(3) 0.9 n C
(4) 1.2 n C
[JEE-Mains-2018]
Ans. (4)
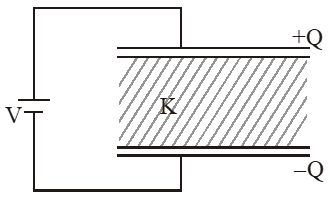$\mathrm{Q}=(\mathrm{k} \mathrm{C}) \mathrm{V}$
$=\left(\frac{5}{3} \times 90 \mathrm{pF}\right)(20 \mathrm{V})$
= 3000 pC
= 3nC
induced charges on dielectric
$\mathrm{Q}_{\mathrm{ind}}=\mathrm{Q}\left(1-\frac{1}{\mathrm{K}}\right)=3 \mathrm{nC}\left(1-\frac{3}{5}\right)=1.2 \mathrm{nC}$
$\mathrm{Q}=(\mathrm{k} \mathrm{C}) \mathrm{V}$
$=\left(\frac{5}{3} \times 90 \mathrm{pF}\right)(20 \mathrm{V})$
= 3000 pC
= 3nC
induced charges on dielectric
$\mathrm{Q}_{\mathrm{ind}}=\mathrm{Q}\left(1-\frac{1}{\mathrm{K}}\right)=3 \mathrm{nC}\left(1-\frac{3}{5}\right)=1.2 \mathrm{nC}$