JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Q. Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2m and m, respectively. The object A moves towards B with a speed 9 m/s and makes an elastic collision with it. Thereafter, B makes completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C.
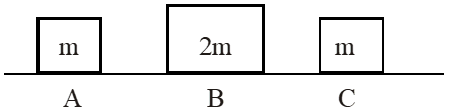 [IIT-JEE-2009]
[IIT-JEE-2009]
 [IIT-JEE-2009]
[IIT-JEE-2009]
Ans. 4m/s


Q. Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are v and 2v, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at A, these two particles will again reach the point A?
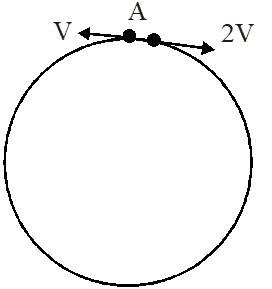 (A) 4 (B) 3 (C) 2 (D) 1
[IIT-JEE-2009]
(A) 4 (B) 3 (C) 2 (D) 1
[IIT-JEE-2009]
 (A) 4 (B) 3 (C) 2 (D) 1
[IIT-JEE-2009]
(A) 4 (B) 3 (C) 2 (D) 1
[IIT-JEE-2009]
Ans. (C)
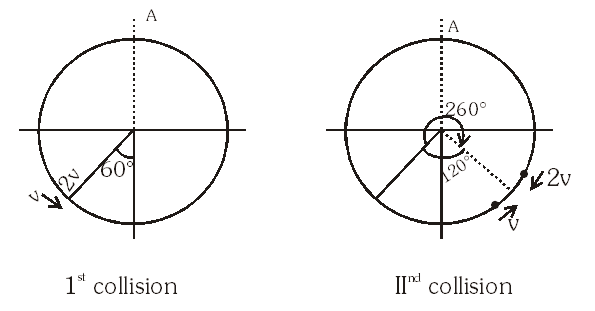 Particle with velocity 'v' covers and angle of $120^{\circ}$ and after collision its velocity become '2v'. It will cover angle of $$240^{\circ}$$
Particle with velocity 'v' covers and angle of $120^{\circ}$ and after collision its velocity become '2v'. It will cover angle of $$240^{\circ}$$
 Particle with velocity 'v' covers and angle of $120^{\circ}$ and after collision its velocity become '2v'. It will cover angle of $$240^{\circ}$$
Particle with velocity 'v' covers and angle of $120^{\circ}$ and after collision its velocity become '2v'. It will cover angle of $$240^{\circ}$$
Q. Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6m. The coordinates of the centres of the different parts are: outer circle (0, 0), left inner circle (–a, a), right inner circle (a, a), vertical line (0, 0) and horizontal line (0, –a). The y-coordinate of the centre of mass of the ink in this drawing is –
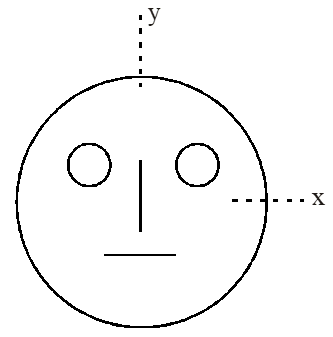 $(\mathrm{A}) \frac{\mathrm{a}}{10}$
(B) $\frac{\mathrm{a}}{8}$
(C) $\frac{\mathrm{a}}{12}$
(D) $\frac{\mathrm{a}}{3}$
[IIT-JEE-2009]
$(\mathrm{A}) \frac{\mathrm{a}}{10}$
(B) $\frac{\mathrm{a}}{8}$
(C) $\frac{\mathrm{a}}{12}$
(D) $\frac{\mathrm{a}}{3}$
[IIT-JEE-2009]
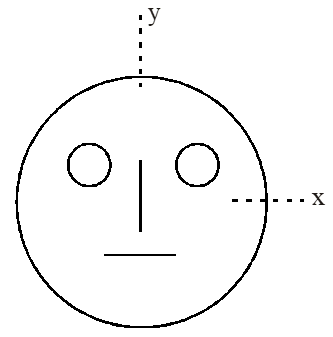 $(\mathrm{A}) \frac{\mathrm{a}}{10}$
(B) $\frac{\mathrm{a}}{8}$
(C) $\frac{\mathrm{a}}{12}$
(D) $\frac{\mathrm{a}}{3}$
[IIT-JEE-2009]
$(\mathrm{A}) \frac{\mathrm{a}}{10}$
(B) $\frac{\mathrm{a}}{8}$
(C) $\frac{\mathrm{a}}{12}$
(D) $\frac{\mathrm{a}}{3}$
[IIT-JEE-2009]
Ans. (A)
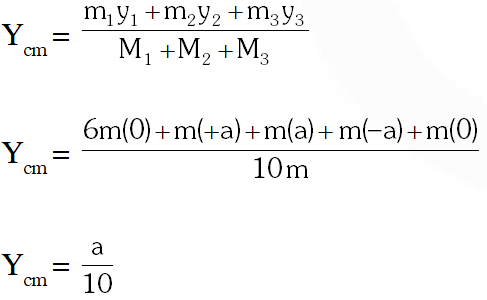
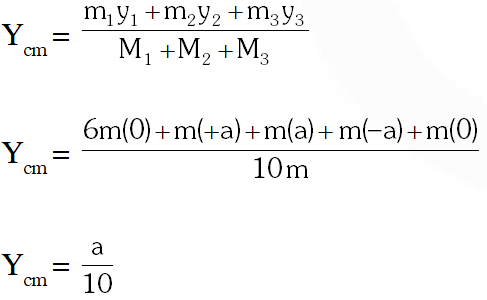
Q. A point mass of 1 kg collides elastically with a stationary point mass of 5 kg. Aftr their collision, the 1 kg mass reverses its direction and moves with a speed of 2 m/s. Which of the following statemet(s) is (are) correct for the system of these two masses ?
(A) Total momentum of the system is 3 kg m/s.
(B) Momentum of 5 kg mass after collision is 4 kg m/s.
(C) Kinetic energy of the centre of mass is 0.75 J.
(D) Total kinetic energy of the system is 4 J.
[IIT-JEE 2010]
Ans. (A,C)
 Conservation of linear momentum
(1) u = – (1) 2 + (5) v 5v –2 = u ... (i)
By definition of ‘e’ $1=\frac{v+2}{u} \Rightarrow v+2=u$... (ii)
By solving above equations $\mathrm{v}=1 \mathrm{ms}^{-1}$ and $\mathrm{u}=3 \mathrm{ms}^{-1}$
For $(\mathrm{A}):$ Total momentum of system $=1 \times \mathrm{u}=3 \mathrm{kg} \mathrm{ms}^{-1}$
For (B) : Momentum of 5 kg after collision $=5(1)=5 \mathrm{kg} \mathrm{ms}^{-1}$
For $(\mathrm{C}): \mathrm{K}_{\mathrm{cm}}=\frac{1}{2}(1+5)\left(\frac{1 \times 3+0}{1+5}\right)=0.75 \mathrm{J}$
For (D) : Total kinetic energy of the system $=\frac{1}{2}(1)(3)^{2}=4.5 \mathrm{J}$
Conservation of linear momentum
(1) u = – (1) 2 + (5) v 5v –2 = u ... (i)
By definition of ‘e’ $1=\frac{v+2}{u} \Rightarrow v+2=u$... (ii)
By solving above equations $\mathrm{v}=1 \mathrm{ms}^{-1}$ and $\mathrm{u}=3 \mathrm{ms}^{-1}$
For $(\mathrm{A}):$ Total momentum of system $=1 \times \mathrm{u}=3 \mathrm{kg} \mathrm{ms}^{-1}$
For (B) : Momentum of 5 kg after collision $=5(1)=5 \mathrm{kg} \mathrm{ms}^{-1}$
For $(\mathrm{C}): \mathrm{K}_{\mathrm{cm}}=\frac{1}{2}(1+5)\left(\frac{1 \times 3+0}{1+5}\right)=0.75 \mathrm{J}$
For (D) : Total kinetic energy of the system $=\frac{1}{2}(1)(3)^{2}=4.5 \mathrm{J}$
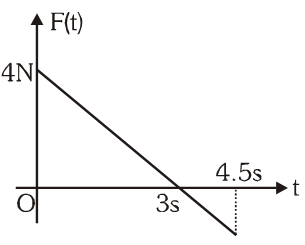
Q. A block of mass 2 kg is free to move along the x–axis. It is at rest and from t=0 onwards it is subjected to a time–dependent force F(t) in the x–direction. The force F(t) varies with t as shown in the figure. The kinetic energy of the block after 4.5 second is
 (A) 4.50 J (B) 7.50 J (C) 5.06 J (D) 14.06 J
[IIT-JEE-2010]
(A) 4.50 J (B) 7.50 J (C) 5.06 J (D) 14.06 J
[IIT-JEE-2010]
 (A) 4.50 J (B) 7.50 J (C) 5.06 J (D) 14.06 J
[IIT-JEE-2010]
(A) 4.50 J (B) 7.50 J (C) 5.06 J (D) 14.06 J
[IIT-JEE-2010]
Ans. (C)
Area in F–t Curve = change in momentum
$\mathrm{P}=\frac{1}{2}(4 \times 3)-\frac{1}{2}(1.5)(2)=\frac{9}{2}$
$\mathrm{V}=\frac{9}{4} \mathrm{m} / \mathrm{s}$
$\mathrm{k.E.}=\frac{1}{2} \times 2 \times\left(\frac{9}{4}\right)^{2} \approx 5.06 \mathrm{J}$
Q. A ball of mass 0.2 kg rests on a vertical post of height 5m. A bullet of mass 0.01 kg, traveling with a velocity V m/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The initial velocity V of the bullet is –
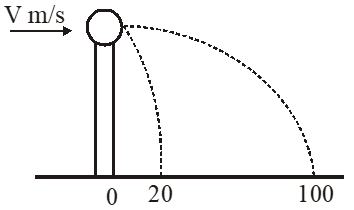 [IIT-JEE 2011]
(A) $250 \mathrm{m} / \mathrm{s}$
(B) $250 \sqrt{2} \mathrm{m} / \mathrm{s}$
(C) $400 \mathrm{m} / \mathrm{s}$
(D) $500 \mathrm{m} / \mathrm{s}$
[IIT-JEE 2011]
(A) $250 \mathrm{m} / \mathrm{s}$
(B) $250 \sqrt{2} \mathrm{m} / \mathrm{s}$
(C) $400 \mathrm{m} / \mathrm{s}$
(D) $500 \mathrm{m} / \mathrm{s}$
 [IIT-JEE 2011]
(A) $250 \mathrm{m} / \mathrm{s}$
(B) $250 \sqrt{2} \mathrm{m} / \mathrm{s}$
(C) $400 \mathrm{m} / \mathrm{s}$
(D) $500 \mathrm{m} / \mathrm{s}$
[IIT-JEE 2011]
(A) $250 \mathrm{m} / \mathrm{s}$
(B) $250 \sqrt{2} \mathrm{m} / \mathrm{s}$
(C) $400 \mathrm{m} / \mathrm{s}$
(D) $500 \mathrm{m} / \mathrm{s}$
Ans. (D)
0.01 V = 0.2 u + 0.01 × 5 u
Time of flight $\mathrm{t}=1$ s; Range for ball $=\mathrm{u} \times \mathrm{t} \Rightarrow 20=\mathrm{u} \times 1 \Rightarrow \mathrm{u}=20 \mathrm{m} / \mathrm{s}$
$\Rightarrow \mathrm{V}=500 \mathrm{m} / \mathrm{s}$
Q. A small block of mass of 0.1 kg lies on a fixed inclined plane PQ which makes an angle $\theta$ with the horizontal. A horizontal force of 1 N acts on the block through its center of mass as shown in the figure. The block remains stationary if (take $\left.\mathrm{g}=10 \mathrm{m} / \mathrm{s}^{2}\right)$
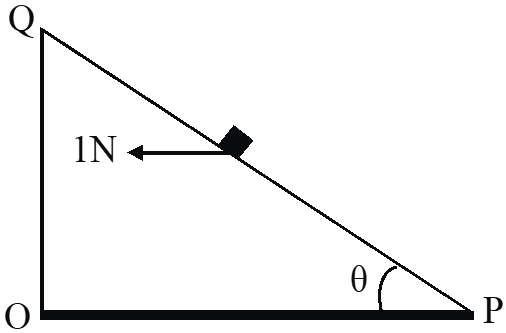 (A) $\theta=45^{\circ}$
(B) $\theta>45^{\circ}$ and a frictional force acts on the block towards P
(C) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
(D) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
[IIT-JEE 2012]
(A) $\theta=45^{\circ}$
(B) $\theta>45^{\circ}$ and a frictional force acts on the block towards P
(C) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
(D) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
[IIT-JEE 2012]
 (A) $\theta=45^{\circ}$
(B) $\theta>45^{\circ}$ and a frictional force acts on the block towards P
(C) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
(D) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
[IIT-JEE 2012]
(A) $\theta=45^{\circ}$
(B) $\theta>45^{\circ}$ and a frictional force acts on the block towards P
(C) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
(D) $\theta>45^{\circ}$ and a frictional force acts on the block towards Q
[IIT-JEE 2012]
Ans. (A,C)
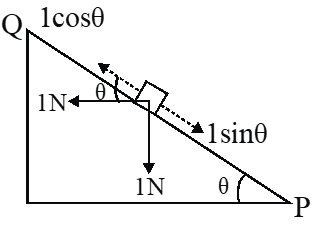 (1) If $\sin \theta=\cos \theta \Rightarrow \theta=45^{\circ} \Rightarrow$ no friction will act and the block will remain at rest.
(2) If $\sin \theta>\cos \theta \Rightarrow \theta>45^{\circ} \Rightarrow$ friction will act towards $\mathrm{Q}$
(3) If $\sin \theta<\cos \theta \Rightarrow \theta<45^{\circ} \Rightarrow$ friction will act towards $\mathrm{P}$
(1) If $\sin \theta=\cos \theta \Rightarrow \theta=45^{\circ} \Rightarrow$ no friction will act and the block will remain at rest.
(2) If $\sin \theta>\cos \theta \Rightarrow \theta>45^{\circ} \Rightarrow$ friction will act towards $\mathrm{Q}$
(3) If $\sin \theta<\cos \theta \Rightarrow \theta<45^{\circ} \Rightarrow$ friction will act towards $\mathrm{P}$
 (1) If $\sin \theta=\cos \theta \Rightarrow \theta=45^{\circ} \Rightarrow$ no friction will act and the block will remain at rest.
(2) If $\sin \theta>\cos \theta \Rightarrow \theta>45^{\circ} \Rightarrow$ friction will act towards $\mathrm{Q}$
(3) If $\sin \theta<\cos \theta \Rightarrow \theta<45^{\circ} \Rightarrow$ friction will act towards $\mathrm{P}$
(1) If $\sin \theta=\cos \theta \Rightarrow \theta=45^{\circ} \Rightarrow$ no friction will act and the block will remain at rest.
(2) If $\sin \theta>\cos \theta \Rightarrow \theta>45^{\circ} \Rightarrow$ friction will act towards $\mathrm{Q}$
(3) If $\sin \theta<\cos \theta \Rightarrow \theta<45^{\circ} \Rightarrow$ friction will act towards $\mathrm{P}$
Q. A bob of mass m, suspended by a string of length $\ell_{1}$ is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length $e_{2}^{\mathrm{T}}$, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum sped required
to complete a full circle in the vertical plane, the ratio $\frac{\ell_{1}}{\ell_{2}}$ is.
[JEE Advanced-2013]
Ans. 5
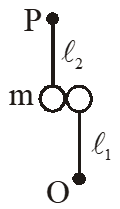 $\sqrt{9 \ell_{1}}=\sqrt{5 \mathrm{g} \ell_{2}} \Rightarrow \frac{\ell_{1}}{\ell_{2}}=5$
$\sqrt{9 \ell_{1}}=\sqrt{5 \mathrm{g} \ell_{2}} \Rightarrow \frac{\ell_{1}}{\ell_{2}}=5$
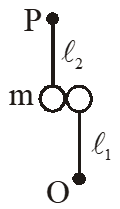 $\sqrt{9 \ell_{1}}=\sqrt{5 \mathrm{g} \ell_{2}} \Rightarrow \frac{\ell_{1}}{\ell_{2}}=5$
$\sqrt{9 \ell_{1}}=\sqrt{5 \mathrm{g} \ell_{2}} \Rightarrow \frac{\ell_{1}}{\ell_{2}}=5$
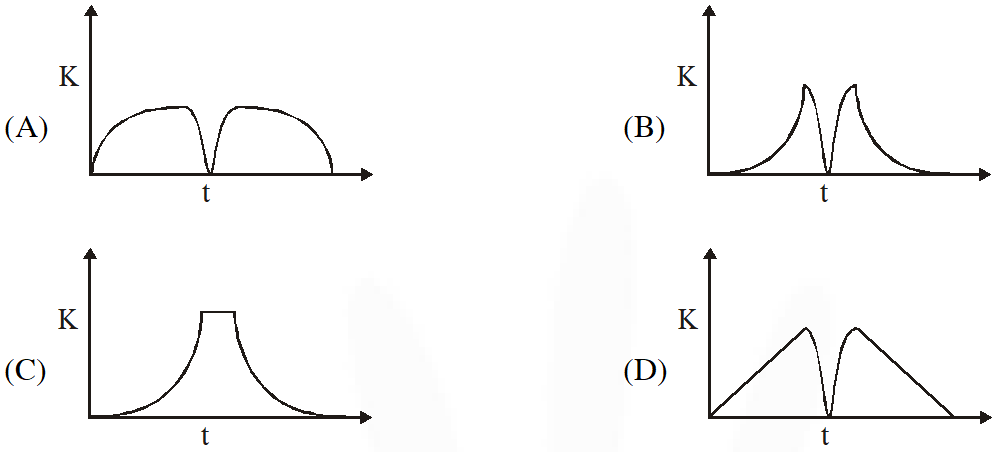
Q. A tennis ball is dropped on a horizontal smooth surface. It bounces back to its original position after hitting the surface. The force on the ball during the collision is proportional to the length of compression of the ball. Which one of the following sketches describes the variation of its kinetic energy K with time t most appropriately ? The figures are only illustrative and not to the scale.
 [JEE Advanced-2014]
[JEE Advanced-2014]
 [JEE Advanced-2014]
[JEE Advanced-2014]
Ans. (B)
During fall, v = 0 + gt
$\mathrm{KE}=\frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2} \mathrm{m}(\mathrm{gt})^{2}$
$\mathrm{KE} \propto \mathrm{t}^{2},$ so graph is upward parabola.
During collision, KE will decrease in compression and increase in reformation.
Finally, during going up KE will decrease.

Q. A block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct ?
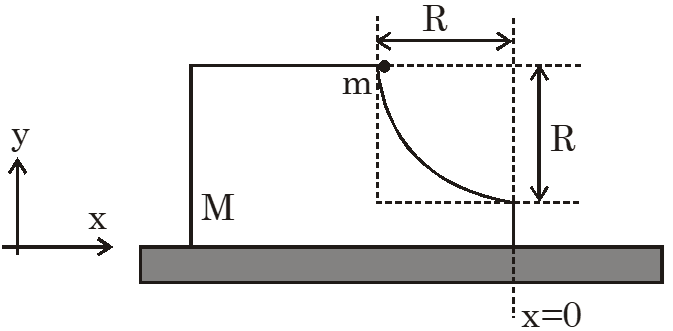 (A) The x component of displacement of the centre of mass of the block M is : $-\frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(B) The position of the point mass is : $\mathrm{x}=-\sqrt{2} \frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(C) The velocity of the point mass m is : $\mathrm{v}=\sqrt{\frac{2 \mathrm{g} \mathrm{R}}{1+\frac{\mathrm{m}}{\mathrm{M}}}}$
(D) The velocity of the block M is : $\mathrm{V}=-\frac{\mathrm{m}}{\mathrm{M}} \sqrt{2 \mathrm{gR}}$
[JEE Advanced-2017]
(A) The x component of displacement of the centre of mass of the block M is : $-\frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(B) The position of the point mass is : $\mathrm{x}=-\sqrt{2} \frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(C) The velocity of the point mass m is : $\mathrm{v}=\sqrt{\frac{2 \mathrm{g} \mathrm{R}}{1+\frac{\mathrm{m}}{\mathrm{M}}}}$
(D) The velocity of the block M is : $\mathrm{V}=-\frac{\mathrm{m}}{\mathrm{M}} \sqrt{2 \mathrm{gR}}$
[JEE Advanced-2017]
 (A) The x component of displacement of the centre of mass of the block M is : $-\frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(B) The position of the point mass is : $\mathrm{x}=-\sqrt{2} \frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(C) The velocity of the point mass m is : $\mathrm{v}=\sqrt{\frac{2 \mathrm{g} \mathrm{R}}{1+\frac{\mathrm{m}}{\mathrm{M}}}}$
(D) The velocity of the block M is : $\mathrm{V}=-\frac{\mathrm{m}}{\mathrm{M}} \sqrt{2 \mathrm{gR}}$
[JEE Advanced-2017]
(A) The x component of displacement of the centre of mass of the block M is : $-\frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(B) The position of the point mass is : $\mathrm{x}=-\sqrt{2} \frac{\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(C) The velocity of the point mass m is : $\mathrm{v}=\sqrt{\frac{2 \mathrm{g} \mathrm{R}}{1+\frac{\mathrm{m}}{\mathrm{M}}}}$
(D) The velocity of the block M is : $\mathrm{V}=-\frac{\mathrm{m}}{\mathrm{M}} \sqrt{2 \mathrm{gR}}$
[JEE Advanced-2017]
Ans. (A,C)
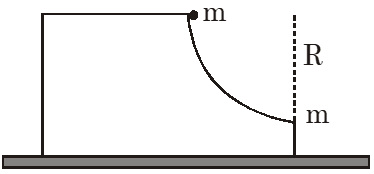 $\mathrm{M}_{\mathrm{s}} \Delta \overline{\mathrm{x}}_{\mathrm{cm}}=\mathrm{m}_{1} \Delta \overline{\mathrm{x}}+\mathrm{m}_{2} \Delta \overline{\mathrm{x}}_{2}$
$0=\mathrm{m}(+\mathrm{R}+\overline{\mathrm{x}})+\mathrm{m} \overline{\mathrm{x}}$
$\overline{\mathrm{x}}=\frac{-\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(A) ans
$\mathrm{M}_{\mathrm{s}} \Delta \overline{\mathrm{x}}_{\mathrm{cm}}=\mathrm{m}_{1} \Delta \overline{\mathrm{x}}+\mathrm{m}_{2} \Delta \overline{\mathrm{x}}_{2}$
$0=\mathrm{m}(+\mathrm{R}+\overline{\mathrm{x}})+\mathrm{m} \overline{\mathrm{x}}$
$\overline{\mathrm{x}}=\frac{-\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(A) ans
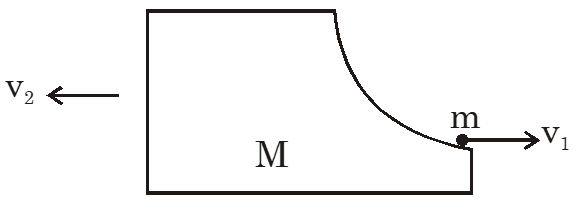 $0=\mathrm{m} \overline{\mathrm{v}}_{1}+\mathrm{M} \overline{\mathrm{v}}_{2}$
$\overline{\mathrm{v}}_{2}=-\frac{\mathrm{m} \overline{\mathrm{v}}_{1}}{\mathrm{M}}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{Mv}_{2}^{2}$
$\mathrm{mgR}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{M}\left(\frac{\mathrm{mv}_{1}}{\mathrm{M}}\right)^{2}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)$
$\sqrt{\frac{2 \mathrm{gR}}{\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)}}=\mathrm{v}_{1}$
$0=\mathrm{m} \overline{\mathrm{v}}_{1}+\mathrm{M} \overline{\mathrm{v}}_{2}$
$\overline{\mathrm{v}}_{2}=-\frac{\mathrm{m} \overline{\mathrm{v}}_{1}}{\mathrm{M}}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{Mv}_{2}^{2}$
$\mathrm{mgR}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{M}\left(\frac{\mathrm{mv}_{1}}{\mathrm{M}}\right)^{2}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)$
$\sqrt{\frac{2 \mathrm{gR}}{\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)}}=\mathrm{v}_{1}$
 $\mathrm{M}_{\mathrm{s}} \Delta \overline{\mathrm{x}}_{\mathrm{cm}}=\mathrm{m}_{1} \Delta \overline{\mathrm{x}}+\mathrm{m}_{2} \Delta \overline{\mathrm{x}}_{2}$
$0=\mathrm{m}(+\mathrm{R}+\overline{\mathrm{x}})+\mathrm{m} \overline{\mathrm{x}}$
$\overline{\mathrm{x}}=\frac{-\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(A) ans
$\mathrm{M}_{\mathrm{s}} \Delta \overline{\mathrm{x}}_{\mathrm{cm}}=\mathrm{m}_{1} \Delta \overline{\mathrm{x}}+\mathrm{m}_{2} \Delta \overline{\mathrm{x}}_{2}$
$0=\mathrm{m}(+\mathrm{R}+\overline{\mathrm{x}})+\mathrm{m} \overline{\mathrm{x}}$
$\overline{\mathrm{x}}=\frac{-\mathrm{mR}}{\mathrm{M}+\mathrm{m}}$
(A) ans
 $0=\mathrm{m} \overline{\mathrm{v}}_{1}+\mathrm{M} \overline{\mathrm{v}}_{2}$
$\overline{\mathrm{v}}_{2}=-\frac{\mathrm{m} \overline{\mathrm{v}}_{1}}{\mathrm{M}}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{Mv}_{2}^{2}$
$\mathrm{mgR}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{M}\left(\frac{\mathrm{mv}_{1}}{\mathrm{M}}\right)^{2}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)$
$\sqrt{\frac{2 \mathrm{gR}}{\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)}}=\mathrm{v}_{1}$
$0=\mathrm{m} \overline{\mathrm{v}}_{1}+\mathrm{M} \overline{\mathrm{v}}_{2}$
$\overline{\mathrm{v}}_{2}=-\frac{\mathrm{m} \overline{\mathrm{v}}_{1}}{\mathrm{M}}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{Mv}_{2}^{2}$
$\mathrm{mgR}=\frac{1}{2} \mathrm{mv}_{1}^{2}+\frac{1}{2} \mathrm{M}\left(\frac{\mathrm{mv}_{1}}{\mathrm{M}}\right)^{2}$
$\operatorname{mg} \mathrm{R}=\frac{1}{2} \mathrm{mv}_{1}^{2}\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)$
$\sqrt{\frac{2 \mathrm{gR}}{\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)}}=\mathrm{v}_{1}$
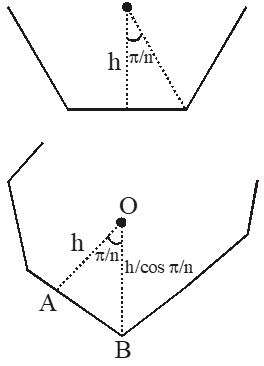
Q. Consider regular polygons with number of sides n = 3, 4, 5 ..... as shown in the figure. The center of mass of all the polygons is at height h from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is D. Then D depends on n and h as :
 (A) $\Delta=\operatorname{hsin}^{2}\left(\frac{\pi}{\mathrm{n}}\right)$
(B) $\Delta=\mathrm{h} \sin \left(\frac{2 \pi}{\mathrm{n}}\right)$
(C) $\Delta=\mathrm{h}\left(\frac{1}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}-1\right)$
(D) $\Delta=h \tan ^{2}\left(\frac{\pi}{2 n}\right)$
[JEE Advanced-2017]
(A) $\Delta=\operatorname{hsin}^{2}\left(\frac{\pi}{\mathrm{n}}\right)$
(B) $\Delta=\mathrm{h} \sin \left(\frac{2 \pi}{\mathrm{n}}\right)$
(C) $\Delta=\mathrm{h}\left(\frac{1}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}-1\right)$
(D) $\Delta=h \tan ^{2}\left(\frac{\pi}{2 n}\right)$
[JEE Advanced-2017]
 (A) $\Delta=\operatorname{hsin}^{2}\left(\frac{\pi}{\mathrm{n}}\right)$
(B) $\Delta=\mathrm{h} \sin \left(\frac{2 \pi}{\mathrm{n}}\right)$
(C) $\Delta=\mathrm{h}\left(\frac{1}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}-1\right)$
(D) $\Delta=h \tan ^{2}\left(\frac{\pi}{2 n}\right)$
[JEE Advanced-2017]
(A) $\Delta=\operatorname{hsin}^{2}\left(\frac{\pi}{\mathrm{n}}\right)$
(B) $\Delta=\mathrm{h} \sin \left(\frac{2 \pi}{\mathrm{n}}\right)$
(C) $\Delta=\mathrm{h}\left(\frac{1}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}-1\right)$
(D) $\Delta=h \tan ^{2}\left(\frac{\pi}{2 n}\right)$
[JEE Advanced-2017]
Ans. (C)
 OA = h
$\mathrm{OB}=\frac{\mathrm{h}}{\cos \frac{\pi}{\mathrm{n}}}$
Initial height of COM = h
Final height of $\mathrm{COM}=\frac{\mathrm{h}}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}$
OA = h
$\mathrm{OB}=\frac{\mathrm{h}}{\cos \frac{\pi}{\mathrm{n}}}$
Initial height of COM = h
Final height of $\mathrm{COM}=\frac{\mathrm{h}}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}$
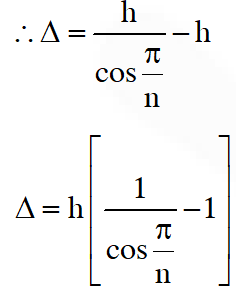
 OA = h
$\mathrm{OB}=\frac{\mathrm{h}}{\cos \frac{\pi}{\mathrm{n}}}$
Initial height of COM = h
Final height of $\mathrm{COM}=\frac{\mathrm{h}}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}$
OA = h
$\mathrm{OB}=\frac{\mathrm{h}}{\cos \frac{\pi}{\mathrm{n}}}$
Initial height of COM = h
Final height of $\mathrm{COM}=\frac{\mathrm{h}}{\cos \left(\frac{\pi}{\mathrm{n}}\right)}$
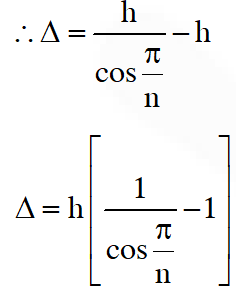
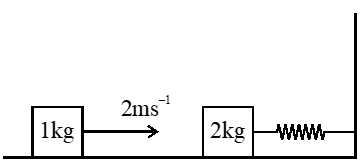
Q. A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 N $\mathrm{M}^{-1}$ and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0 m $\mathrm{s}^{-1}$ collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _____.
 [JEE Advanced-2018]
[JEE Advanced-2018]
 [JEE Advanced-2018]
[JEE Advanced-2018]
Ans. (2.09 M)
$\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}=2 \pi \mathrm{sec}$
block returns to original position in $\frac{\mathrm{T}}{2}=\pi \mathrm{sec}$
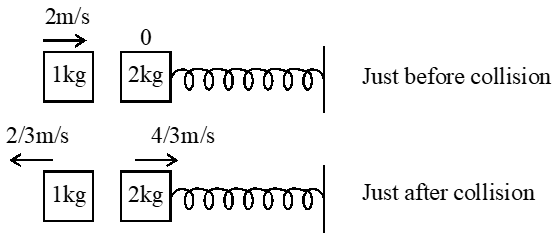 $\mathrm{d}=\frac{2}{3}(\pi)=\frac{2}{3}(3.14)=2.0933 \mathrm{m}$
d = 2.09 m
$\mathrm{d}=\frac{2}{3}(\pi)=\frac{2}{3}(3.14)=2.0933 \mathrm{m}$
d = 2.09 m
 $\mathrm{d}=\frac{2}{3}(\pi)=\frac{2}{3}(3.14)=2.0933 \mathrm{m}$
d = 2.09 m
$\mathrm{d}=\frac{2}{3}(\pi)=\frac{2}{3}(3.14)=2.0933 \mathrm{m}$
d = 2.09 m
Q. A solid horizontal surface is covered with a thin layer of oil. A rectangular block of mass m = 0.4kg is at rest on this surface. An impulse of 1.0 N s is applied to the block at time to t = 0 so that it starts moving along the x-axis with a velocity v(t) = $v_{0} \mathrm{e}^{-t / \tau}$, where $v_{0}$ is a constant and $\tau=4 \mathrm{s}$. The displacement of the block, in metres, at $t=\tau$ is................... Take e $^{-1}$ = 0.37 ?
[JEE Advanced-2018]
Ans. 6.3
 $\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\mathrm{v}_{0}=\frac{\mathrm{J}}{\mathrm{m}}=2.5 \mathrm{m} / \mathrm{s}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{v}_{0} \mathrm{e}^{-\mathrm{t} / \tau}$
$\int_{0}^{\mathrm{x}} \mathrm{dx}=\mathrm{v}_{0} \int_{0}^{\mathrm{r}} \mathrm{e}^{-t / \tau} \mathrm{dt} \quad \int \mathrm{e}^{-\mathrm{x}} \mathrm{d} \mathrm{x}=\frac{\mathrm{e}^{-\mathrm{x}}}{-1}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\mathrm{v}_{0}=\frac{\mathrm{J}}{\mathrm{m}}=2.5 \mathrm{m} / \mathrm{s}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{v}_{0} \mathrm{e}^{-\mathrm{t} / \tau}$
$\int_{0}^{\mathrm{x}} \mathrm{dx}=\mathrm{v}_{0} \int_{0}^{\mathrm{r}} \mathrm{e}^{-t / \tau} \mathrm{dt} \quad \int \mathrm{e}^{-\mathrm{x}} \mathrm{d} \mathrm{x}=\frac{\mathrm{e}^{-\mathrm{x}}}{-1}$
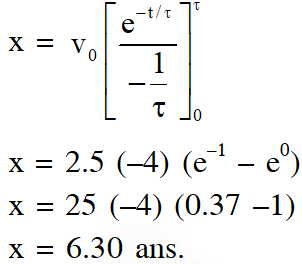
 $\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\mathrm{v}_{0}=\frac{\mathrm{J}}{\mathrm{m}}=2.5 \mathrm{m} / \mathrm{s}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{v}_{0} \mathrm{e}^{-\mathrm{t} / \tau}$
$\int_{0}^{\mathrm{x}} \mathrm{dx}=\mathrm{v}_{0} \int_{0}^{\mathrm{r}} \mathrm{e}^{-t / \tau} \mathrm{dt} \quad \int \mathrm{e}^{-\mathrm{x}} \mathrm{d} \mathrm{x}=\frac{\mathrm{e}^{-\mathrm{x}}}{-1}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\mathrm{v}_{0}=\frac{\mathrm{J}}{\mathrm{m}}=2.5 \mathrm{m} / \mathrm{s}$
$\mathbf{V}=\mathbf{V}_{0} \mathbf{e}^{-\mathbf{t} / \tau}$
$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{v}_{0} \mathrm{e}^{-\mathrm{t} / \tau}$
$\int_{0}^{\mathrm{x}} \mathrm{dx}=\mathrm{v}_{0} \int_{0}^{\mathrm{r}} \mathrm{e}^{-t / \tau} \mathrm{dt} \quad \int \mathrm{e}^{-\mathrm{x}} \mathrm{d} \mathrm{x}=\frac{\mathrm{e}^{-\mathrm{x}}}{-1}$
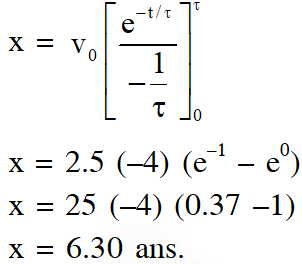
Comments
sneha
April 9, 2024, 1:32 p.m.
you are providing much bettter papers as compare to other online resourses
sneha
April 9, 2024, 10:12 a.m.
you are providing much bettter papers as compare to other online resourses
sneha
April 9, 2024, 6:35 a.m.
you are providing much bettter papers as compare to other online resourses
sneha
April 9, 2024, 6:35 a.m.
you are providing much bettter papers as compare to other online resourses
vinay
Jan. 8, 2021, 5:23 p.m.
good helped me in celarinng jee i got air in physics just by these questions thank u .....haha just kidding its a good worksheet to solve
