JEE Advanced Previous Year Questions of Chemistry with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Chemistry will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Simulator
Previous Years JEE Advance Questions
Q. Plots showing the variation of the rate constant (k) with temperature (T) are given
below. The plot that follows Arrhenius equation is –
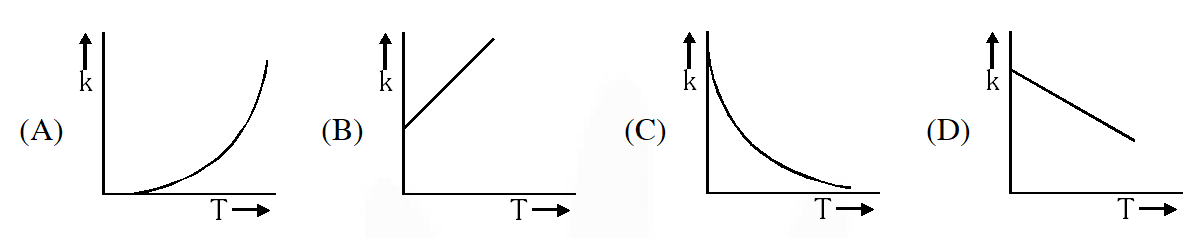 [JEE 2010]
[JEE 2010]
 [JEE 2010]
[JEE 2010]
Ans. (A)
Arrhenius equation : $\mathrm{k}=\mathrm{Ae}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}}$
(taking A and $\mathrm{E}_{\mathrm{a}}$ to be constant, differentiating w.r.t. T)
$\frac{\mathrm{d} \mathrm{k}}{\mathrm{d} \mathrm{T}}=\left[\frac{\mathrm{AE}_{\mathrm{a}}}{\mathrm{RT}^{2}}\right] \mathrm{e}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}}$
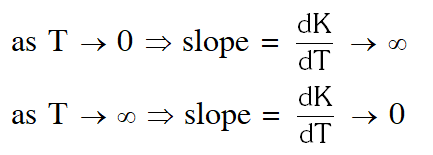 assuming A and $\mathrm{E}_{\mathrm{a}}$ to be constant theoretically, the plot should be
assuming A and $\mathrm{E}_{\mathrm{a}}$ to be constant theoretically, the plot should be
 But
But No such option is given. Now experimentally, A and $\mathrm{E}_{\mathrm{a}}$ both vary with temperature and k increases as T increases and become very large at infinite temperature. Hence option (A) is correct.
No such option is given. Now experimentally, A and $\mathrm{E}_{\mathrm{a}}$ both vary with temperature and k increases as T increases and become very large at infinite temperature. Hence option (A) is correct.
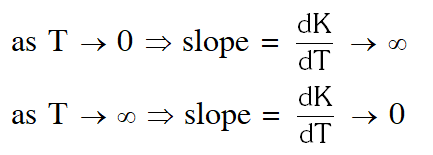 assuming A and $\mathrm{E}_{\mathrm{a}}$ to be constant theoretically, the plot should be
assuming A and $\mathrm{E}_{\mathrm{a}}$ to be constant theoretically, the plot should be
 But
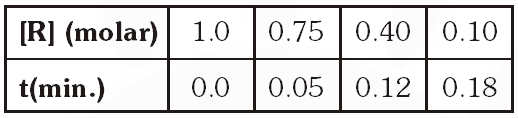
ButQ. The concentration of R in the reaction $\mathrm{R} \rightarrow \mathrm{P}$ was measured as a function of time and the following data is obtained :
 [JEE 2010]
[JEE 2010]
 [JEE 2010]
[JEE 2010]
Ans. 0
 Zero order reaction because rate is constant with time.
Alternative solution : By hit and trial method, assuming the reaction is of zero order, putting given data in integrated expression for zero order.
Zero order reaction because rate is constant with time.
Alternative solution : By hit and trial method, assuming the reaction is of zero order, putting given data in integrated expression for zero order.
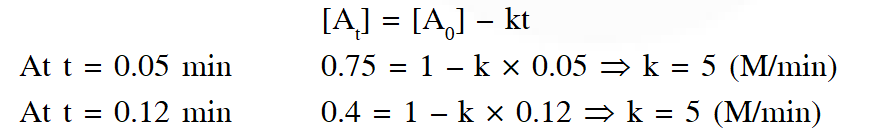 the value of k is same from different data so reaction is zero order reaction.
the value of k is same from different data so reaction is zero order reaction.
 Zero order reaction because rate is constant with time.
Alternative solution : By hit and trial method, assuming the reaction is of zero order, putting given data in integrated expression for zero order.
Zero order reaction because rate is constant with time.
Alternative solution : By hit and trial method, assuming the reaction is of zero order, putting given data in integrated expression for zero order.
 the value of k is same from different data so reaction is zero order reaction.
the value of k is same from different data so reaction is zero order reaction.
Q. For the first order reaction
$2 \mathrm{N}_{2} \mathrm{O}_{5}(\mathrm{g}) \longrightarrow 4 \mathrm{NO}_{2}(\mathrm{g})+\mathrm{O}_{2}(\mathrm{g})$
(A) the concentration of the reactant decreases exponentially with time
(B) the half-life of the reaction decreases with increasing temperature.
(C) the half-life of the reaction depends on the initial concentration of the reactant.
(D) the reaction proceeds to 99.6% completion in eight half-life duration.
[JEE 2011]
Ans. (A,B,D)
$\mathrm{A}_{\mathrm{t}}=\mathrm{A}_{0} \mathrm{e}^{-\mathrm{kt}}$
for option (D)
$\frac{1}{\mathrm{t}_{1 / 2}} \ln \frac{100}{50}=\frac{1}{\mathrm{t}_{99.6 \%}} \ln \frac{100}{0.4}$
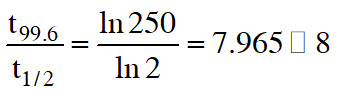
Q. An organic compound undergoes first-order decomposition . The time taken for its decomposition to 1/8 and 1/10 of its initial concentration are $$
\mathrm{t}_{1 / 8} \text { and } \mathrm{t}_{1 / 10}
$$ What is the value of $$
\frac{\left[\mathrm{t}_{1 / 8}\right]}{\mathrm{t}_{1 / 10}} \times 10 ?\left(\text { take } \log _{10} 2=0.3\right)
$$
[JEE 2012]
Ans. 9
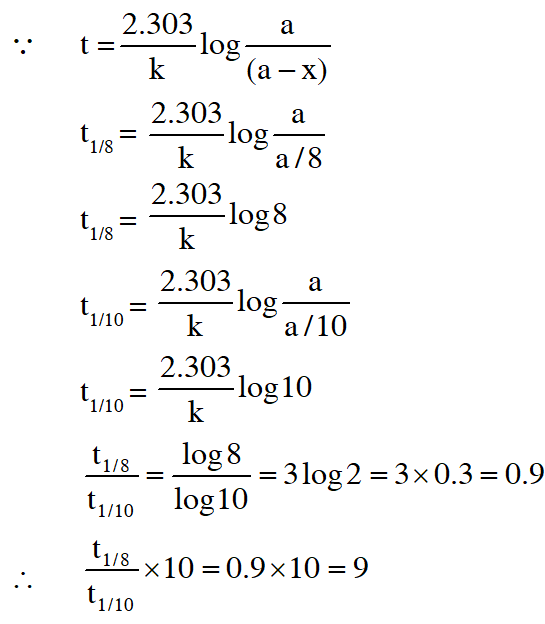
Q. In the reaction :
$$
\mathrm{P}+\mathrm{Q} \longrightarrow \mathrm{R}+\mathrm{S}
$$
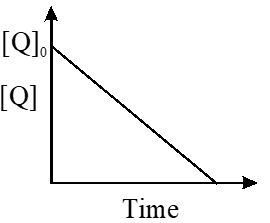 the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The
concentration of Q varies with reaction time as shown in the figure. The overall order of the
reaction is -
(A) 2 (B) 3 (C) 0 (D) 1
[JEE 2013]
the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The
concentration of Q varies with reaction time as shown in the figure. The overall order of the
reaction is -
(A) 2 (B) 3 (C) 0 (D) 1
[JEE 2013]
 the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The
concentration of Q varies with reaction time as shown in the figure. The overall order of the
reaction is -
(A) 2 (B) 3 (C) 0 (D) 1
[JEE 2013]
the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The
concentration of Q varies with reaction time as shown in the figure. The overall order of the
reaction is -
(A) 2 (B) 3 (C) 0 (D) 1
[JEE 2013]
Ans. 9
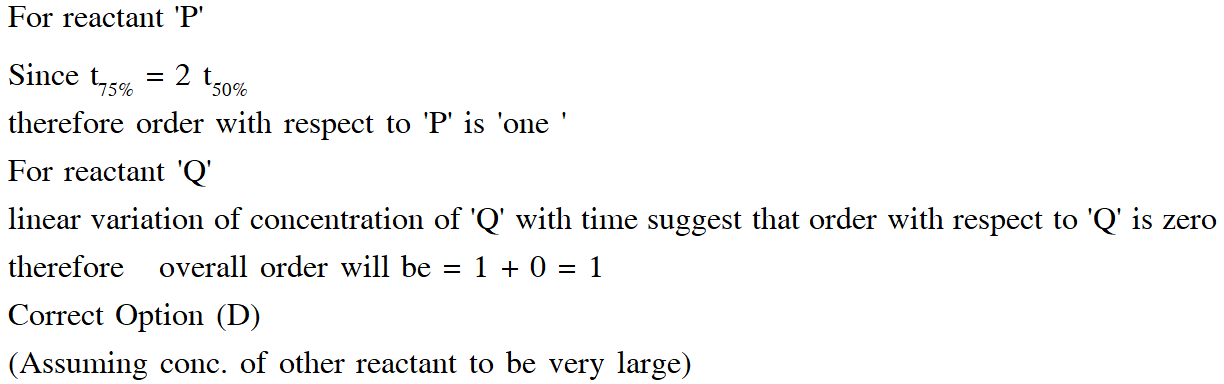
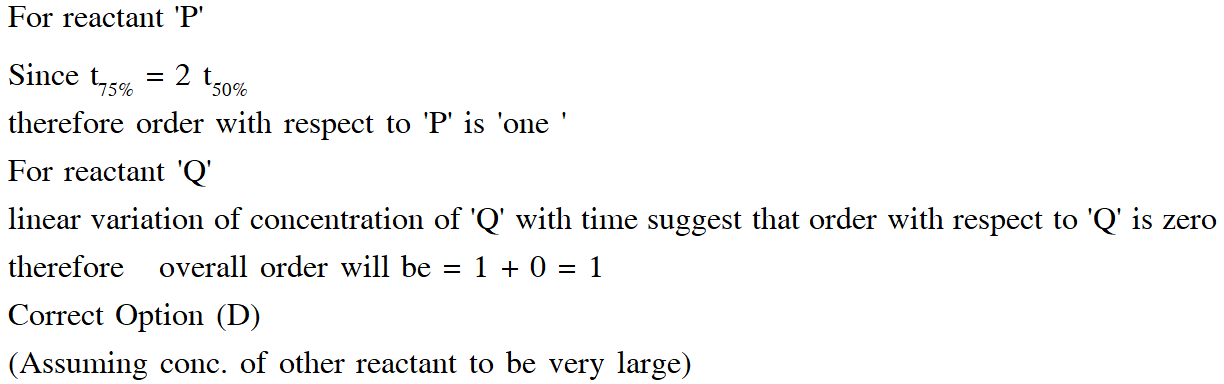
Q. For the elementary reaction $$
\mathrm{M} \rightarrow \mathrm{N}$$, the rate of disappearance of M increases by a factor of 8 upon doubling the concentration of M. The order of the reaction with respect to M is
(A) 4 (B) 3(C) 2(D) 1
[JEE 2014]
Ans. (D)
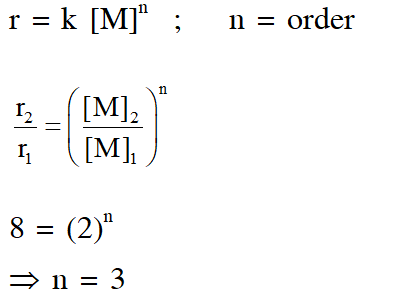
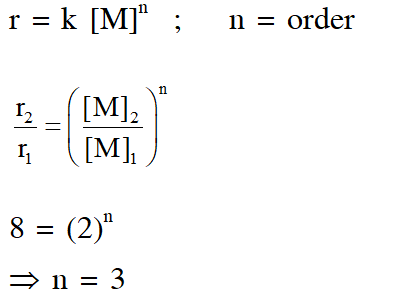
Q. In dilute aqueous $$
\mathrm{H}_{2} \mathrm{SO}_{4}$$ , the complex diaquodioxalatoferrate(II) is oxidized by $\mathrm{MnO}_{4}^{-}$.For this reaction, the ratio of the rate of change of $$
\left[\mathrm{H}^{+}\right]$$ to the rate of change of [MnO4–] is.
[JEE 2015]
Ans. (B)
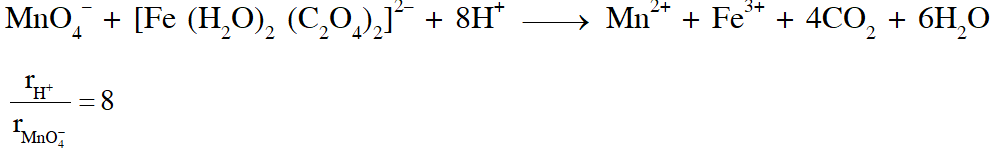
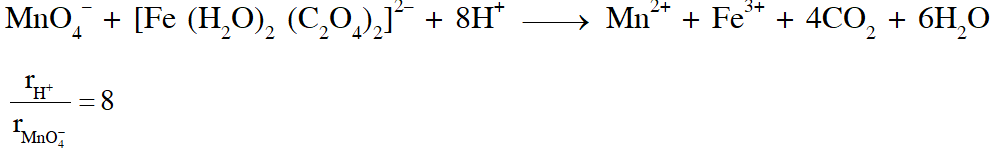
Q. The % yield of ammonia as a function of time in the reaction
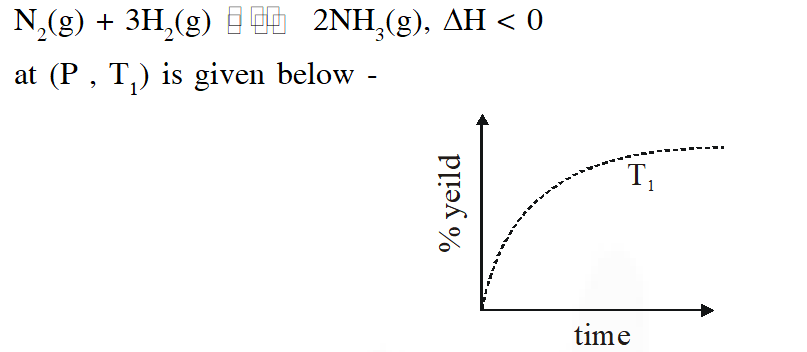 If this reaction is conducted at $\left(P, T_{2}\right)$, with $\mathrm{T}_{2}>\mathrm{T}_{1}$, the % yield of ammonia as a function of time is represented by –
If this reaction is conducted at $\left(P, T_{2}\right)$, with $\mathrm{T}_{2}>\mathrm{T}_{1}$, the % yield of ammonia as a function of time is represented by –
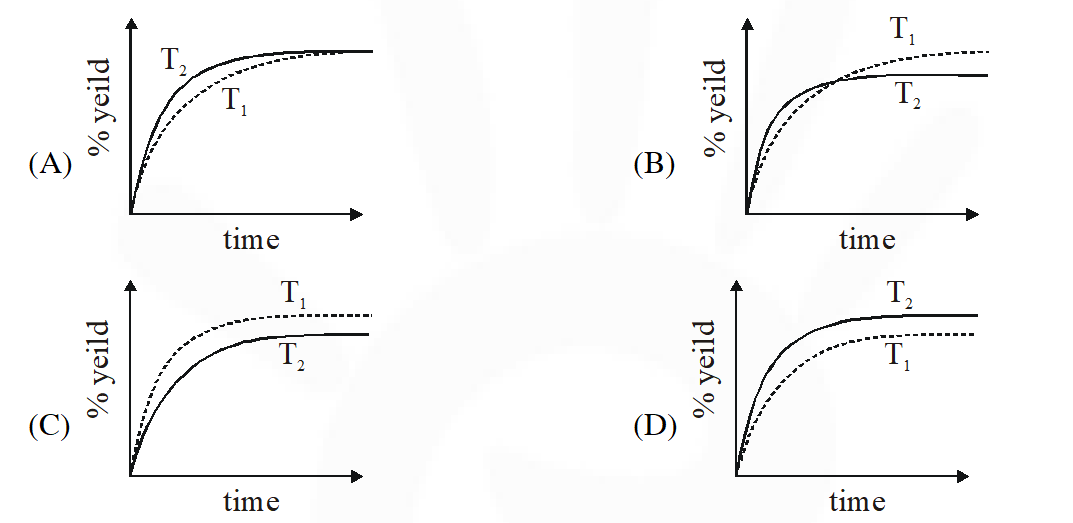 [JEE 2015]
[JEE 2015]
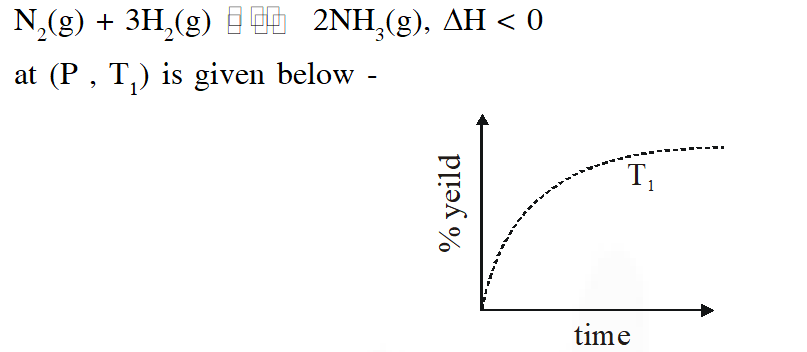 If this reaction is conducted at $\left(P, T_{2}\right)$, with $\mathrm{T}_{2}>\mathrm{T}_{1}$, the % yield of ammonia as a function of time is represented by –
If this reaction is conducted at $\left(P, T_{2}\right)$, with $\mathrm{T}_{2}>\mathrm{T}_{1}$, the % yield of ammonia as a function of time is represented by –
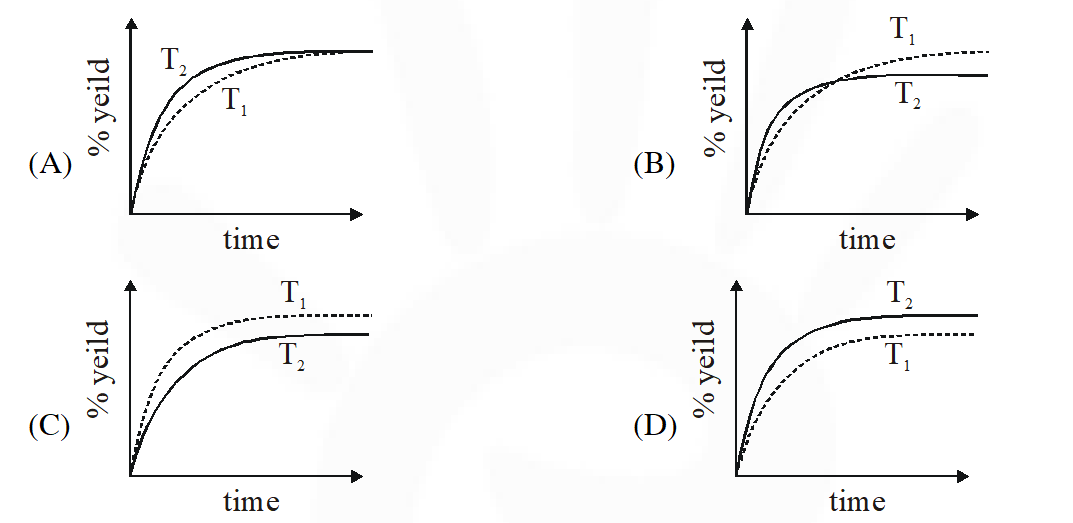 [JEE 2015]
[JEE 2015]
Ans. (B)
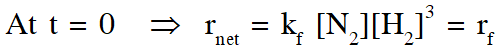 $\therefore$ % yield will increase in initial stages due to increase in net speed
As time proceeds $\Rightarrow \mathrm{r}_{\mathrm{net}}=\mathrm{k}_{\mathrm{f}}\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}-\mathrm{k}_{\mathrm{b}}\left[\mathrm{NH}_{3}\right]^{2}$
On increasing temp., $\mathrm{k}_{\mathrm{f}} \& \mathrm{k}_{\mathrm{b}}$ increase
but increase of $\mathrm{k}_{\mathrm{b}}$ is more
so % yield will decrease
% yield will increase in initial stage due to enhance speed but as time proceeds , final yield is governed by thermodynamics due to which yield decrease since reaction is exothermic
$\therefore$ % yield will increase in initial stages due to increase in net speed
As time proceeds $\Rightarrow \mathrm{r}_{\mathrm{net}}=\mathrm{k}_{\mathrm{f}}\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}-\mathrm{k}_{\mathrm{b}}\left[\mathrm{NH}_{3}\right]^{2}$
On increasing temp., $\mathrm{k}_{\mathrm{f}} \& \mathrm{k}_{\mathrm{b}}$ increase
but increase of $\mathrm{k}_{\mathrm{b}}$ is more
so % yield will decrease
% yield will increase in initial stage due to enhance speed but as time proceeds , final yield is governed by thermodynamics due to which yield decrease since reaction is exothermic
Q. For a first order reaction A(g) 2B(g) + C(g) at constant volume and 300 K, the
total pressure at the beginning (t = 0) and at time t are P0 and Pt, respectively. Initially, only A
is present with concentration [A]0, and $t_{1 / 3}$ is the time required for the partial pressure
of A to reach $1 / 3^{\mathrm{rd}}$ of its initial value. The correct option(s) is (are) :-
(Assume that all these gases behave as ideal gases)
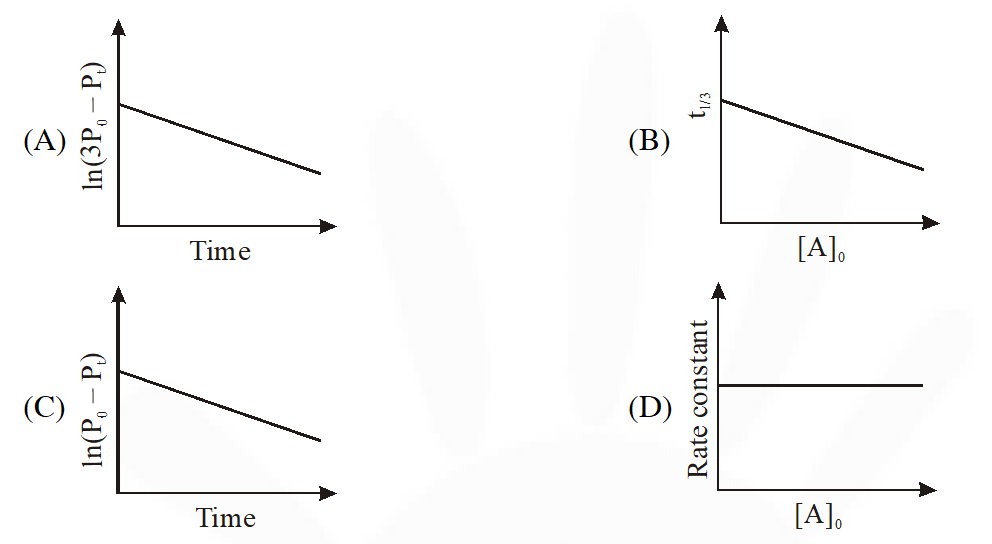 [JEE Advance 2018]
[JEE Advance 2018]
 [JEE Advance 2018]
[JEE Advance 2018]
Ans. (A,D)
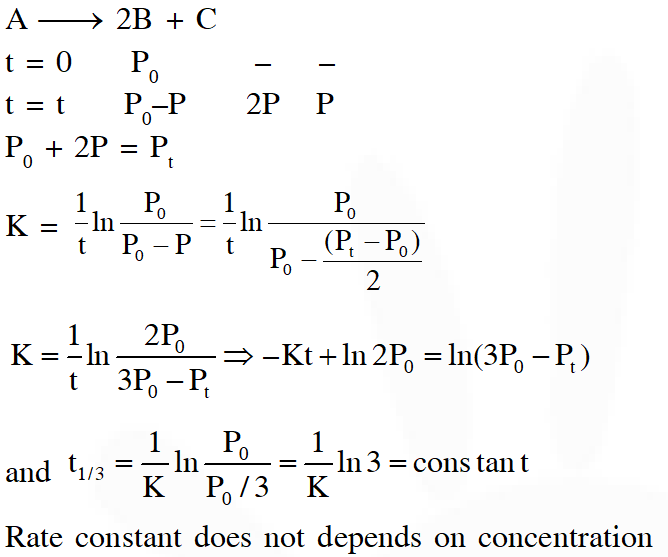
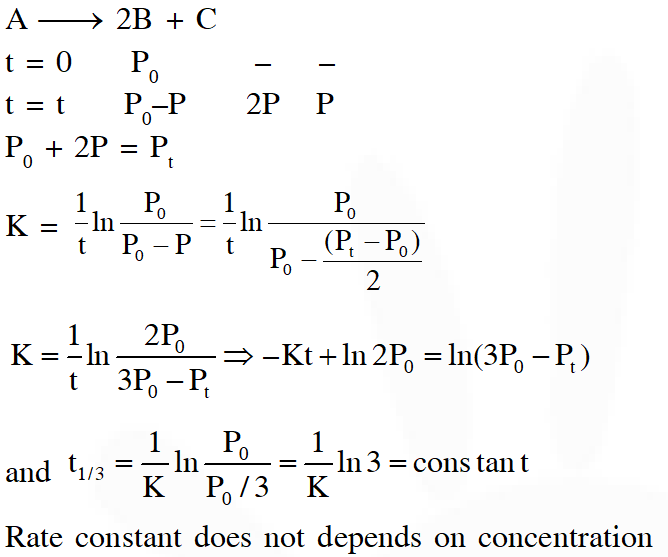
Q. Consider the following reversible reaction,
$\mathrm{A}(\mathrm{g})+\mathrm{B}(\mathrm{g}) \square \mathrm{AB}(\mathrm{g})$
The activition energy of the backward reaction exceeds that of the forward reaction by 2RT $\left(\text { in } \mathrm{J} \mathrm{mol}^{-1}\right)$. If the pre-exponential factor of the forward reaction is 4 times that of the reverse reaction, the absolute value of $\Delta \mathrm{G}^{\theta}$(in J mol–1) for the reaction at 300 K is____.
(Given ; ln (2) = 0.7, RT = 2500 J $\mathrm{mol}^{-1}$ at 300 K and G is the Gibbs energy)
[JEE Advance 2018]
Ans. 8500
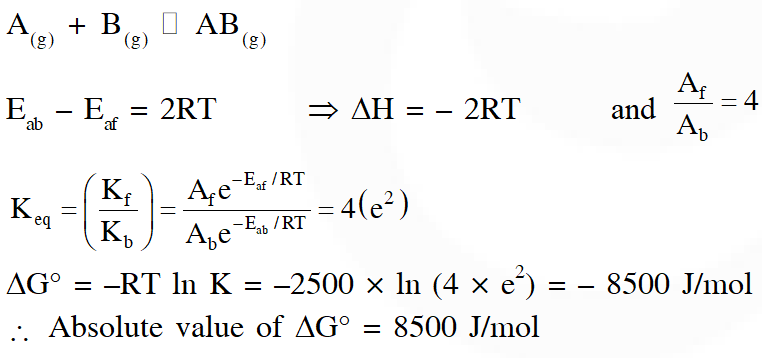
Comments
M.Jhaya Lavannyah,IAS
June 25, 2021, 7:26 p.m.
Management,please read comments so that you can resolve issues.
Anonymous
June 25, 2021, 7:25 p.m.
I don’t think management reads comments.If they have read,most of the issues must have been resolved by now.
Hritik
Sept. 13, 2020, 6:33 p.m.
the questions arent very clear .plz try to solve those techinical issues
