JEE Main Previous Year Papers Questions of Chemistry with Solutions are available at eSaral. Practicing JEE Mains chapter wise questions of Chemistry will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. The half life period of a first order chemical reaction is 6.93 minutes. The time required for the completion of 99% of the chemical reaction will be (log 2 = 0.301) :-
(1) 46.06 minutes (2) 460.6 minutes (3) 230.3 minutes (4) 23.03 minutes
[aieee-2009]
Ans. (1)
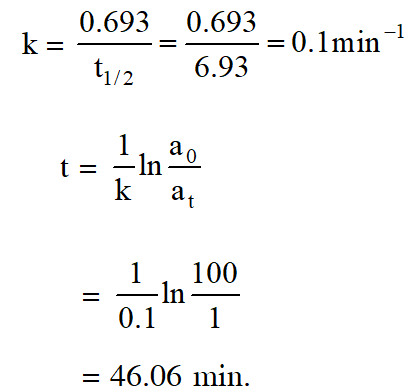
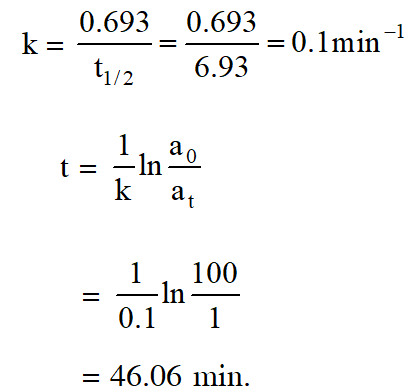
Q. The time for half life period of a certain reaction A Products is 1 hour, when the initial concentration of the reactant 'A' is 2.0 mol L–1, How much time does it take for its concentration to come from 0.50 to 0.25 mol L–1 if it is a zero order reaction?
(1) 1 h
(2) 4 h
(3) 0.5 h
(4) 0.29.
[aieee-2010]
Ans. (4)
For zero order reaction
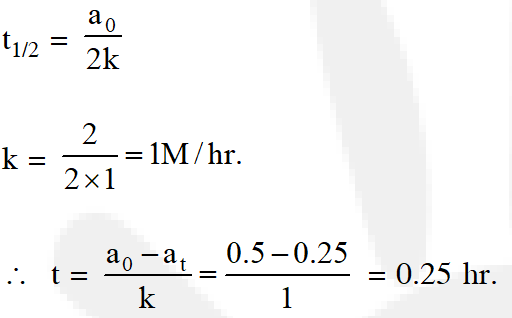
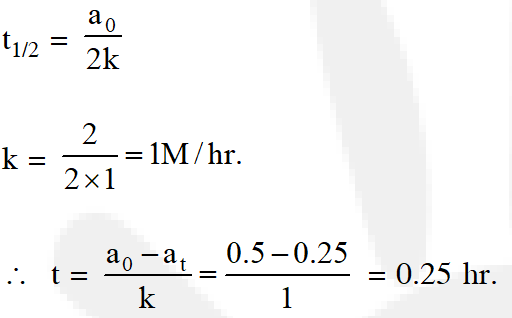
Q. Consider the reaction:
$\mathrm{Cl}_{2}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{S}(\mathrm{aq}) \rightarrow \mathrm{S}(\mathrm{s})+2 \mathrm{H}^{+}(\mathrm{aq})+2 \mathrm{Cl}^{-}(\mathrm{aq})$
The rate equation for this reaction is rate = $\mathrm{k}\left[\mathrm{Cl}_{2}\right]\left[\mathrm{H}_{2} \mathrm{S}\right]$
Which of these mechanisms is/are consistent with this rate equation?
 [aieee-2010]
[aieee-2010]
 [aieee-2010]
[aieee-2010]
Ans. (1)


Q. A reactant (A) forms two products :
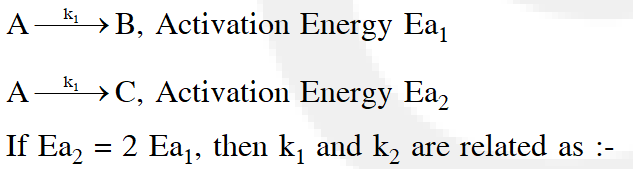 (1) $\mathrm{k}_{1}=2 \mathrm{k}_{2} \mathrm{e}^{\mathrm{E}_{2} / \mathrm{RT}}$
(2) $\mathrm{k}_{1}=\mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
(3) $\mathrm{k}_{2}=\mathrm{k}_{1} \mathrm{e}^{\mathrm{Ea}_{2} / \mathrm{RT}}$
(4) $\mathrm{k}_{1}=\mathrm{A} \mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
[aieee-2011]
(1) $\mathrm{k}_{1}=2 \mathrm{k}_{2} \mathrm{e}^{\mathrm{E}_{2} / \mathrm{RT}}$
(2) $\mathrm{k}_{1}=\mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
(3) $\mathrm{k}_{2}=\mathrm{k}_{1} \mathrm{e}^{\mathrm{Ea}_{2} / \mathrm{RT}}$
(4) $\mathrm{k}_{1}=\mathrm{A} \mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
[aieee-2011]
 (1) $\mathrm{k}_{1}=2 \mathrm{k}_{2} \mathrm{e}^{\mathrm{E}_{2} / \mathrm{RT}}$
(2) $\mathrm{k}_{1}=\mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
(3) $\mathrm{k}_{2}=\mathrm{k}_{1} \mathrm{e}^{\mathrm{Ea}_{2} / \mathrm{RT}}$
(4) $\mathrm{k}_{1}=\mathrm{A} \mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
[aieee-2011]
(1) $\mathrm{k}_{1}=2 \mathrm{k}_{2} \mathrm{e}^{\mathrm{E}_{2} / \mathrm{RT}}$
(2) $\mathrm{k}_{1}=\mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
(3) $\mathrm{k}_{2}=\mathrm{k}_{1} \mathrm{e}^{\mathrm{Ea}_{2} / \mathrm{RT}}$
(4) $\mathrm{k}_{1}=\mathrm{A} \mathrm{k}_{2} \mathrm{e}^{\mathrm{Ea}_{1} / \mathrm{RT}}$
[aieee-2011]
Ans. (2)
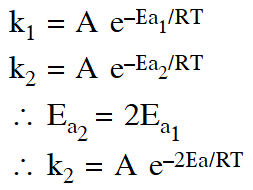
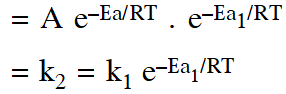
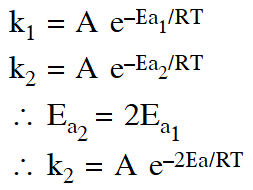
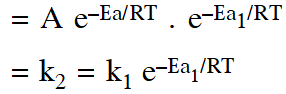
Q. The rate of a chemical reaction doubles for every $10^{\circ} \mathrm{C}$ rise of temperature. If the temperature is raised by $50^{\circ} \mathrm{C}, \mathrm$ the rate of the reaction increases by about :-
(1) 32 times (2) 64 times (3) 10 times (4) 24 times
[aieee-2011]
Ans. (1)
$\mathrm{k}_{2}=\mathrm{k}_{1}(2)^{5}=32 \mathrm{k}_{1}$
Q. For a first order reaction, (A) products, the concentration of A changes from 0.1M to 0.025M in 40 minutes. The rate of reaction when the concentration of A is 0.01 M is :
(1) $1.73 \times 10^{-4} \mathrm{M} / \mathrm{min}$
(2) $1.73 \times 10^{-5} \mathrm{M} / \mathrm{min}$
(3) $3.47 \times 10^{-4} \mathrm{M} / \mathrm{min}$
(4) $3.47 \times 10^{-5} \mathrm{M} / \mathrm{m}$
[aieee-2012]
Ans. (3)
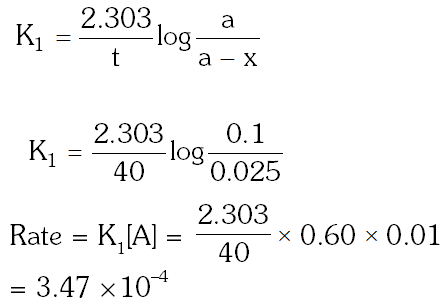
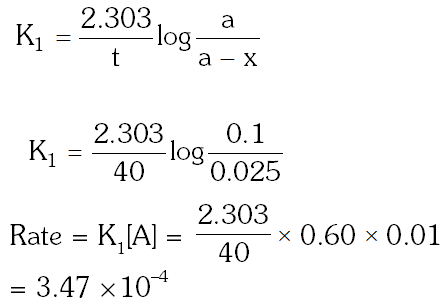
Q. The rate of a reaction doubles when its temperature changes from 300 K to 310 K. Activation energy of such a reaction will be
$\left(\mathrm{R}=8.314 \mathrm{JK}^{-1} \mathrm{mol}^{-1} \text { and } \log 2=0.301\right)$
(1) $53.6 \mathrm{kJ} \mathrm{mol}^{-1}$
(2) $48.6 \mathrm{kJ} \mathrm{mol}^{-1}$
(3) $58.5 \mathrm{kJ} \mathrm{mol}^{-1}$
(4) $60.5 \mathrm{kJ} \mathrm{mol}^{-1}$
[J-main 2013]
Ans. (1)
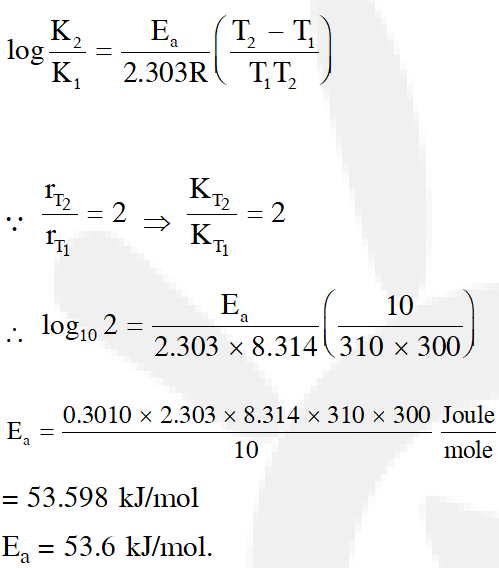
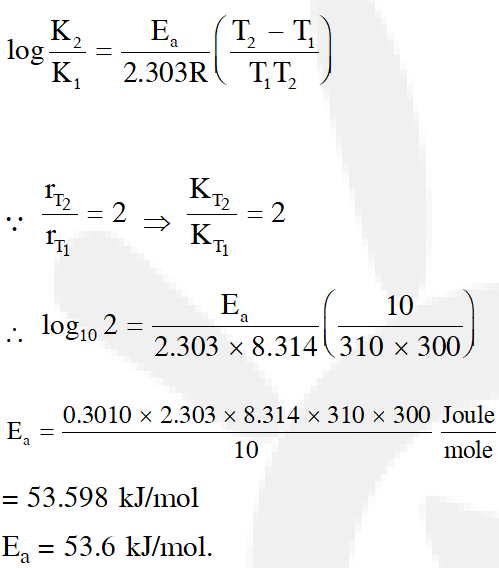
Q. For the non-stoichiometre reaction 2A + B C + D, the following kinetic data were obtained in three separate experiments, all at 298 K.
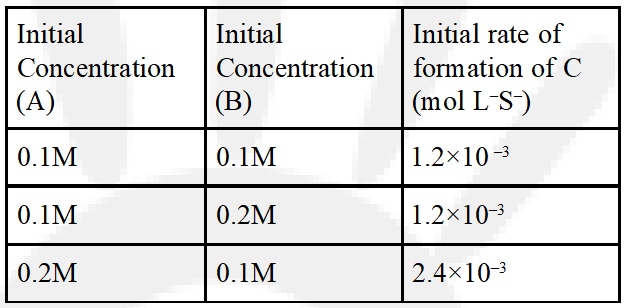 (1) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]^{2}$
(2) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]$
(3) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]$
(4) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]^{2}[\mathrm{B}]$
[J-main 2014]
(1) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]^{2}$
(2) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]$
(3) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]$
(4) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]^{2}[\mathrm{B}]$
[J-main 2014]
 (1) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]^{2}$
(2) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]$
(3) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]$
(4) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]^{2}[\mathrm{B}]$
[J-main 2014]
(1) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]^{2}$
(2) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]$
(3) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}][\mathrm{B}]$
(4) $\frac{\mathrm{dc}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}]^{2}[\mathrm{B}]$
[J-main 2014]
Ans. (2)
Q. Higher order (>3) reactions are rare due to :-
(1) shifting of equilibrium towards reactants due to elastic collision
(2) loss of active species on collision
(3) low probability of simultaneous collision of all the reacting species
(4) increase in entropy and activation energy as more molecules are involved.
[JEE-MAIN-(Offline) 2015]
Ans. (3)
Higher order (>3) reaction are rare due to low probability of simulatneous collision of more than three molecuels.
Q. The reaction
$2 \mathrm{N}_{2} \mathrm{O}_{5}(\mathrm{g}) \rightarrow 4 \mathrm{NO}_{2}(\mathrm{g})+\mathrm{O}_{2}(\mathrm{g})$
follows first order kinetics. The pressure of a vessel containing only $\mathrm{N}_{2} \mathrm{O}_{5}$ was found to increase from 50 mm Hg to 87.5 mm Hg in 30 min. The pressure exerted by the gases after 60 min. will be (Assume temperature remains constant)
(1) 106.25 nm Hg
(2) 116.25 nm Hg
(3) 125 mm Hg
(4) 150 mm Hg
[JEE-MAIN (Online)2015]
Ans. (2)
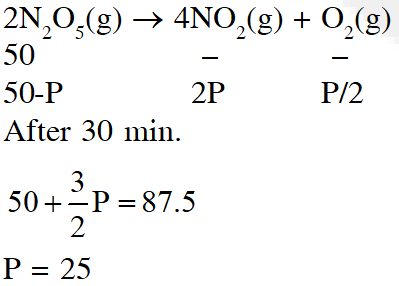
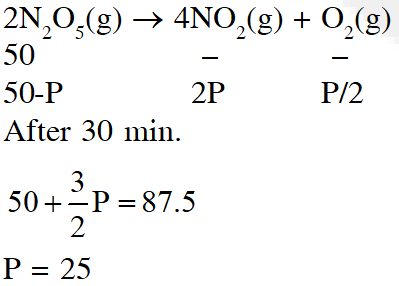
Q. For the equilibrium, $\mathrm{A}(\mathrm{g}) \square \mathrm{B}(\mathrm{g}), \Delta \mathrm{H}$ is is –40 kJ/mol. If the ratio of the activation energies of the forward $\left(\mathrm{E}_{\mathrm{f}}\right)$ and reverse $\left(\mathrm{E}_{\mathrm{b}}\right)$ reactions is $\frac{2}{3}$ then :-
(1) $\mathrm{E}_{\mathrm{f}}=60 \mathrm{kJ} / \mathrm{mol} ; \mathrm{E}_{\mathrm{b}}=100 \mathrm{kJ} / \mathrm{mol}$
$|(2) \mathrm{E}_{\mathrm{f}}=30 \mathrm{kJ} / \mathrm{mol} ; \mathrm{E}_{\mathrm{b}}=70 \mathrm{kJ} / \mathrm{mol}$
(3) $\mathrm{E}_{\mathrm{f}}=80 \mathrm{kJ} / \mathrm{mol} ; \mathrm{E}_{\mathrm{b}}=120 \mathrm{kJ} / \mathrm{mol}$
(4) $\mathrm{E}_{\mathrm{f}}=70 \mathrm{kJ} / \mathrm{mol} ; \mathrm{E}_{\mathrm{b}}=30 \mathrm{kJ} / \mathrm{mol}$
[JEE-MAIN (Online)2015]
Ans. (3)
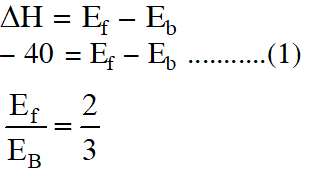
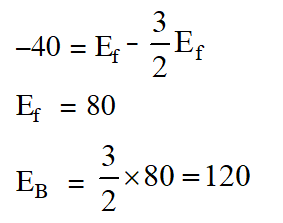
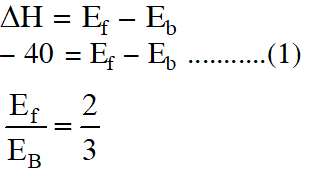
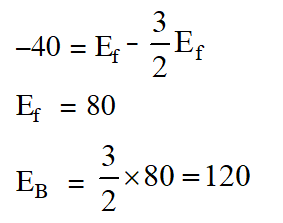
Q. Decomposition of $\mathrm{H}_{2} \mathrm{O}_{2}$ follows a first order reaction. In fifty minutes the concentration of $\mathrm{H}_{2} \mathrm{O}_{2}$ decreases from 0.5 to 0.125 M in one such decomposition. When the concentration of $\mathrm{H}_{2} \mathrm{O}_{2}$ reaches 0.05 M, the rate of formation of $\mathrm{O}_{2}$ will be :-
 [JEE - Main 2016]
[JEE - Main 2016]
Ans. (3)
$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})} \longrightarrow \mathrm{H}_{2} \mathrm{O}_{(\mathrm{aq})}+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g})$
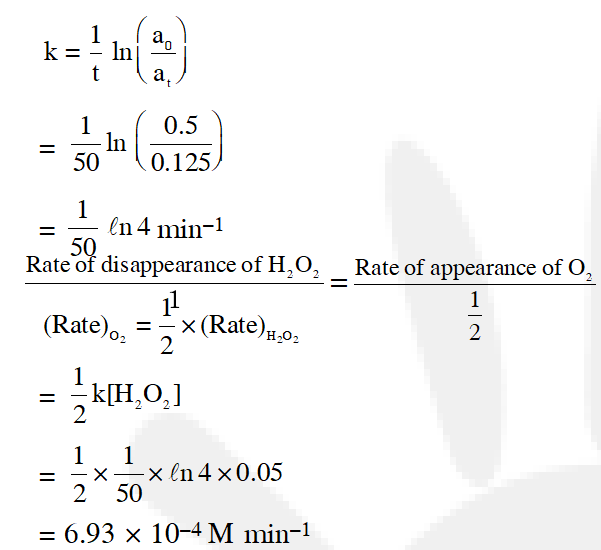
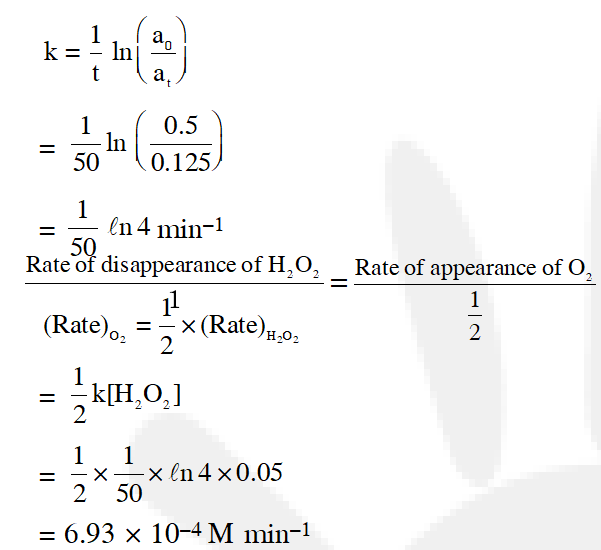
Q. Two reactions R1 and R2 have identical pre-exponential factors. Activation energy of $\mathrm{R}_{1}$ exceeds that of $\mathrm{R}_{2}$ by 10 kJ $\mathrm{mol}^{-1}$. If k1 and k2 are rate constants for reactions $\mathrm{R}_{1}$ and $\mathrm{R}_{2}$ respectively at 300 K, then ln $\left(\mathrm{k}_{2} / \mathrm{k}_{1}\right)$ is equal to :-
(1) 8 (2) 12 (3) 6 (4) 4
[JEE - Main 2017]
Ans. (4)
From arrhenius equation,
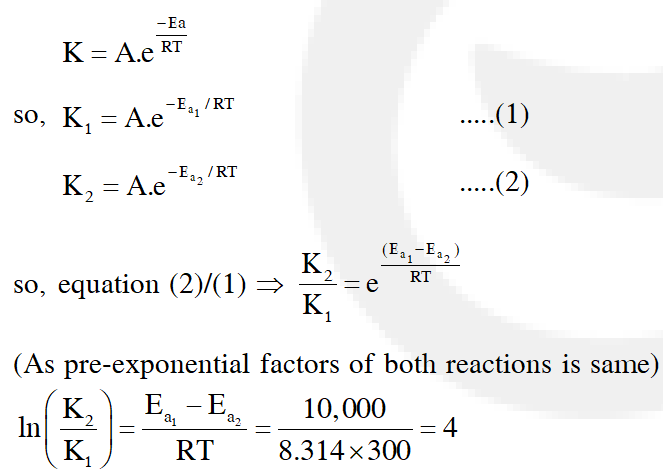
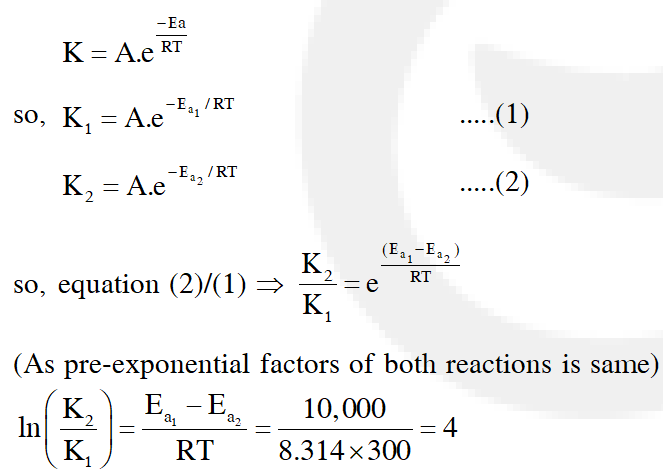
Q. At $518^{\circ} \mathrm{C}$, the rate of decomposition of a sample of gaseous acetaldehyde, initially at a pressure of 363 Torr, was 1.00 Torr $\mathrm{s}^{-1}$ when 5% had reacted and 0.5 Torr s–1 when 33% had reacted. The order of the reaction is :
(1)3
(2) 1
(3) 0
(4) 2
[JEE - Main 2018]
Ans. (4)
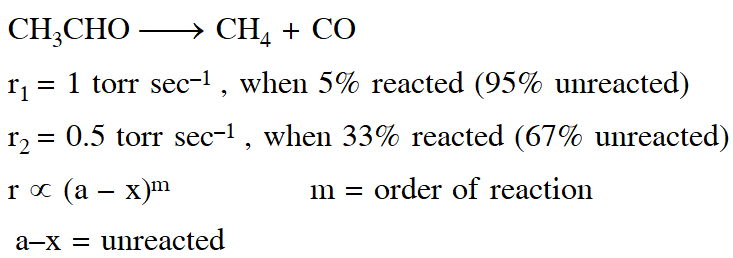
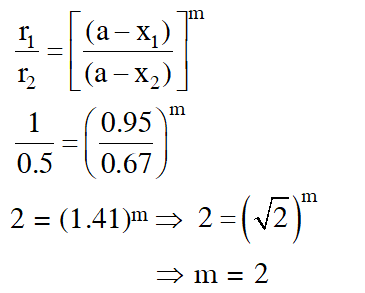
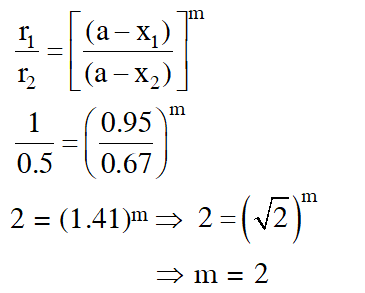
Comments
Kamal AB
May 4, 2021, 10:49 a.m.
In 5th question what is that. Yellow marked lineee can anybody reply
Lalu Prasad Yadav
Feb. 15, 2021, 5:11 p.m.
Thank you for giving this special opportunity to solve this paper, becoz you opened my eyes. Th
Vineet
Sept. 28, 2020, 7:21 a.m.
Now I am appearing for Jee mains 2021 January and I like to use this .
Syed Ruvii
Aug. 21, 2020, 3:37 p.m.
Answer to the jee main 2015 question is given wrong.....right one is 106.25
Harshitha
Aug. 19, 2020, 8:25 p.m.
It's very much useful
It helps to know our weak areas and improve better
CICADA 101
July 4, 2020, 5:30 p.m.
we have begun the hunt for talented individuals .
hello !
CICADA 101
we are the one
Aditya
May 29, 2020, 4:24 p.m.
Very awesome page where all previous year Questions are at a place.
Sir pls 2019 and 2020 ke questions bhi add kr
dijeye
Aditya Raj Kaushik
May 18, 2020, 9:20 p.m.
Best content and methods of explanation questions are easy I solved all very easily
dheepaganesan
May 18, 2020, 3:46 p.m.
awesome problems thanks for the support but make the notes and solution more easy and complete some solutions
