JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Paragraph for Question 7 and 8
A tangent PT is drawn to the circle $x^{2}+y^{2}=4$ at the point $P(\sqrt{3}, 1) .$ A straight line L, perpendicular to PT is a tangent to the circle $(x-3)^{2}+y^{2}=1$
Paragraph "X"
Let S be the circle in the xy-plane defined by the equation $x^{2}+y^{2}=4$.
(There are two question based on Paragraph "X", the question given below is one of them)
Paragraph "X"
Let S be the circle in the xy-plane defined by the equation $x^{2}+y^{2}=4$
(There are two questions based on Paragraph "X", the question given below is one of them)
Q. Tangents drawn from the point $\mathrm{P}(1,8)$ to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{x}-4 \mathrm{y}-11=0$ touch the circle at the points $\mathrm{A}$ and $\mathrm{B}$. The equation of the circumcircle of the triangle $\mathrm{PAB}$ is
(A) $\mathrm{x}^{2}+\mathrm{y}^{2}+4 \mathrm{x}-6 \mathrm{y}+19=0$
(B) $\mathrm{x}^{2}+\mathrm{y}^{2}-4 \mathrm{x}-10 \mathrm{y}+19=0$
(C) $x^{2}+y^{2}-2 x+6 y-29=0$
(D) $x^{2}+y^{2}-6 x-4 y+19=0$
[JEE 2009, 3]
Ans. (B)
Q. The centres of two circles $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ each of unit radius are at a distance of 6 units from eachother. Let $\mathrm{P}$ be the mid point of the line segment joining the centres of $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ and $\mathrm{C}$ be a circle touching circles $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ externally. If a common tangent to $\mathrm{C}_{1}$ and $\mathrm{C}$ passing through $\mathrm{P}$ is also a common tangent to $\mathrm{C}_{2}$ and $\mathrm{C}$, then the radius of the circle $\mathrm{C}$ is
[JEE 2009, 4]
Ans. 8
Q. Two parallel chords of a circle of radius 2 are at a distance $\sqrt{3}+1$ apart. If the chords subtend at the center, angles of $\frac{\pi}{\mathrm{k}}$ and $\frac{2 \pi}{\mathrm{k}},$ where $\mathrm{k}>0,$ then the value of $[\mathrm{k}]$ is
[Note : [k] denotes the largest integer less than or equal to k]
[JEE 10, 3M]
Ans. 3
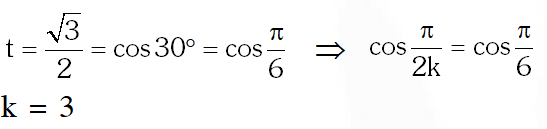
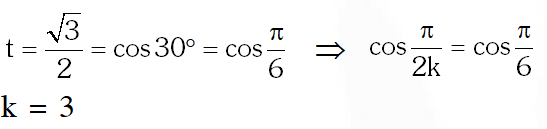
Q. The circle passing through the point (–1,0) and touching the y-axis at (0,2) also passes through the point –
(A) $\left(-\frac{3}{2}, 0\right)$
(B) $\left(-\frac{5}{2}, 2\right)$
(C) $\left(-\frac{3}{2}, \frac{5}{2}\right)$
(D) (–4,0)
[JEE 2011, 3M, –1M]
Ans. (D)
Family of circle which touches $y$ -axis at $(0,2)$ is
$x^{2}+(y-2)^{2}+\lambda x=0$
Passing through $(-1,0)$
$\Rightarrow 1+4-\lambda=0 \quad \Rightarrow \quad \lambda=5$
$\therefore \quad x^{2}+y^{2}+5 x-4 y+4=0$
$\quad$ which satisfy the point $(-4,0)$
Q. The straight line $2 \mathrm{x}-3 \mathrm{y}=1$ divides the circular region $\mathrm{x}^{2}+\mathrm{y}^{2} \leq 6$ into two parts. If $S=\left\{\left(2, \frac{3}{4}\right),\left(\frac{5}{2}, \frac{3}{4}\right),\left(\frac{1}{4},-\frac{1}{4}\right),\left(\frac{1}{8}, \frac{1}{4}\right)\right\},$ then the number of point(s) in Slying inside the smaller part is
[JEE 2011, 4M]
Ans. 2
for origin : 2 × 0 – 3 × 0 – 1 = – 1 (–ve)
for origin : 2 × 0 – 3 × 0 – 1 = – 1 (–ve)
Q. The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 \mathrm{x}-5 \mathrm{y}=20$ to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9 \mathrm{is}-$
(A) $20\left(\mathrm{x}^{2}+\mathrm{y}^{2}\right)-36 \mathrm{x}+45 \mathrm{y}=0$
(B) $20\left(\mathrm{x}^{2}+\mathrm{y}^{2}\right)+36 \mathrm{x}-45 \mathrm{y}=0$
(C) $36\left(x^{2}+y^{2}\right)-20 x+45 y=0$
(D) $36\left(x^{2}+y^{2}\right)+20 x-45 y=0$
[JEE 2012, 3M, –1M]
Ans. (A)
Q. A common tangent of the two circles is
(A) x = 4
(B) y = 2
(C) $x+\sqrt{3} y=4$
(D) $x+2 \sqrt{2} y=6$
[JEE 2012, 3M, –1M]
Ans. (D)
Q. A possible equation of L is
(A) $x-\sqrt{3} y=1$
(B) $x+\sqrt{3} y=1$
(C) $x-\sqrt{3} y=-1$
(D) $x+\sqrt{3} y=5$
[JEE 2012, 3M, –1M]
Ans. (A)
Equation of tangent at $P$ will be $\sqrt{3} x+y=4$
Slope of line L will be $\frac{1}{\sqrt{3}}$
Let equation of $\mathrm{L}$ be $: y=\frac{\mathrm{x}}{\sqrt{3}}+\mathrm{c}$
$\Rightarrow \quad x-\sqrt{3} y+\sqrt{3} c=0$
Now this $L$ is tangent to $2^{\text {nd }}$ circle
So $\frac{3+\sqrt{3} c}{2}=\pm 1 \quad \Rightarrow \quad c=-\frac{1}{\sqrt{3}}$
or $c=-\frac{5}{\sqrt{3}}$
using $\quad c=-\frac{1}{\sqrt{3}}$
$y=\frac{x}{\sqrt{3}}-\frac{1}{\sqrt{3}} \Rightarrow x-\sqrt{3} y=1 .$ Hence $(\mathrm{A})$
Q. Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length $2 \sqrt{7}$ or y-axis is (are)
(A) $x^{2}+y^{2}-6 x+8 y+9=0$
(B) $x^{2}+y^{2}-6 x+7 y+9=0$
(C) $\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{x}-8 \mathrm{y}+9=0$
(D) $x^{2}+y^{2}-6 x-7 y+9=0$
[JEE(Advanced) 2013, 3, (–1)]
Ans. (A,C)
Q. A circle S passes through the point $(0,1)$ and is orthogonal to the circles $(x-1)^{2}+y^{2}=16$ and $x^{2}+y^{2}=1 .$ Then $:-$
(1) radius of S is 8
(B) radius of S is 7
(3) centre of S is (–7, 1)
(D) centre is S is (–8, 1)
[JEE(Advanced)-2014, 3]
Ans. (B)
Q. Let RS be the diameter of the circle x^{2}+y^{2}=1, where S is the point (1,0). Let P be a variable point (other than R and S) on the circle and tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. then the locus of E passes through the point(s)-
(A) $\left(\frac{1}{3}, \frac{1}{\sqrt{3}}\right)$
(B) $\left(\frac{1}{4}, \frac{1}{2}\right)$
(C) $\left(\frac{1}{3},-\frac{1}{\sqrt{3}}\right)$
(D) $\left(\frac{1}{4},-\frac{1}{2}\right)$ (D) $\left(\frac{1}{4},-\frac{1}{2}\right)$
[JEE(Advanced)-2016]
Ans. (A,C)
Q. For how many values of p, the circle $x^{2}+y^{2}+2 x+4 y-p=0$ and the coordinate axes have exactly three common points ?
[JEE(Advanced)-2017]
Ans. (2)
Q. Let T be the line passing through the points P(–2, 7) and Q(2, –5). Let $\mathrm{F}_{2}$ be the set of all pairs of circles $\left(\mathrm{S}_{1}, \mathrm{S}_{2}\right)$ such that T is tangents to $\mathrm{S}_{1}$ at P and tangent to $\mathrm{S}_{2}$ at Q, and also such that $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ touch each other at a point, say, M. Let $\mathrm{E}_{1}$ be the set representing the locus of M as the pair $\left(\mathrm{S}_{1}, \mathrm{S}_{2}\right)$ varies in $\mathrm{F}_{1}$. Let the set of all straight line segments joining a pair of distinct points of $E_{1}$ and passing through the point R(1, 1) be $\mathrm{F}_{2}$. Let $E_{2}$ be the set of the mid-points of the line segments in the set $\mathrm{F}_{2}$. Then, which of the following statement(s) is (are) TRUE ?
(A) The point $(-2,7)$ lies in $\mathrm{E}_{1}$
(B) The point $\left(\frac{4}{5}, \frac{7}{5}\right)$ does NOT lie in $\mathrm{E}_{2}$
(C) The point $\left(\frac{1}{2}, 1\right)$ lies in $\mathrm{E}_{2}$
(D) The point $\left(0, \frac{3}{2}\right)$ does NOT lie in $\mathrm{E}_{1}$
[JEE(Advanced)-2018]
Ans. (D)
Q. Let $\mathrm{E}_{1} \mathrm{E}_{2}$ and $\mathrm{F}_{1} \mathrm{F}_{2}$ be the chord of S passing through the point $\mathrm{P}_{0}(1,1)$ and parallel to the $\mathrm{x}-$ axis and the $\mathrm{y}$ -axis, respectively. Let $\mathrm{G}_{1} \mathrm{G}_{2}$ be the chord of S passing through $\mathrm{P}_{0}$ and having slop $-1 .$ Let the tangents to $\mathrm{S}$ at $\mathrm{E}_{1}$ and $\mathrm{E}_{2}$ meet at $\mathrm{E}_{3}$, the tangents of $\mathrm{S}$ at $\mathrm{F}_{1}$ and $\mathrm{F}_{2}$ meet at $\mathrm{F}_{3},$ and the tangents to $\mathrm{S}$ at $\mathrm{G}_{1}$ and $\mathrm{G}_{2}$ meet at $\mathrm{G}_{3} .$ Then, the points $\mathrm{E}_{3}, \mathrm{F}_{3}$ and $\mathrm{G}_{3}$ lie on the curve
(A) x + y = 4
(B) $(\mathrm{x}-4)^{2}+(\mathrm{y}-4)^{2}=16$
(C) (x – 4) (y – 4) = 4
(D) xy = 4
[JEE(Advanced)-2018]
Ans. (A )
Q. Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve –
(A) $(\mathrm{x}+\mathrm{y})^{2}=3 \mathrm{xy}$
(B) $\mathrm{x}^{2 / 3}+\mathrm{y}^{2 / 3}=2^{4 / 3}$
(C) $x^{2}+y^{2}=2 x y$
(D) $x^{2}+y^{2}=x^{2} y^{2}$
[JEE(Advanced)-2018]
Ans. 15
Tangent at $\mathrm{P}(2 \cos \theta, 2 \sin \theta)$ is $\mathrm{xcos} \theta+\mathrm{y} \sin \theta=2$
$\mathrm{M}(2 \sec \theta, 0)$ and $\mathrm{N}(0,2 \csc \theta)$
Let midpoint be $(\mathrm{h}, \mathrm{k})$
$\mathrm{h}=\sec \theta, \quad \mathrm{k}=\csc \theta$
$\frac{1}{\mathrm{h}^{2}}+\frac{1}{\mathrm{k}^{2}}=1$
$\frac{1}{\mathrm{x}^{2}}+\frac{1}{\mathrm{y}^{2}}=1$
Tangent at $\mathrm{P}(2 \cos \theta, 2 \sin \theta)$ is $\mathrm{xcos} \theta+\mathrm{y} \sin \theta=2$
$\mathrm{M}(2 \sec \theta, 0)$ and $\mathrm{N}(0,2 \csc \theta)$
Let midpoint be $(\mathrm{h}, \mathrm{k})$
$\mathrm{h}=\sec \theta, \quad \mathrm{k}=\csc \theta$
$\frac{1}{\mathrm{h}^{2}}+\frac{1}{\mathrm{k}^{2}}=1$
$\frac{1}{\mathrm{x}^{2}}+\frac{1}{\mathrm{y}^{2}}=1$
Comments
<script>alert("Valuable resource, Sir")</script>
Feb. 27, 2024, 6:35 a.m.
<script>alert("Sir please update more questions of later years")</script)
eSaral
Sept. 15, 2021, 3:38 p.m.
very helpful and comprehensive content for students aiming competetive exams such as JOINT ENTRANCE EXAM including main and advance the paraphased content helps students to appear for many questions and increase their perspection