Combination of capacitors - Series, Parallel Combinations - eSaral

Hey, do you want to learn about the combination of capacitors? If so. Then keep reading.

Combination of capacitors

The process of replacing a combination of capacitors by a single equivalent capacitor is called the Combination of capacitors or grouping of capacitors.

Capacitors in parallel

1. Capacitors are said to be connected in parallel between two points if it is possible to proceed from one point to another point along different paths.
2. Capacitors are said to be in parallel if the potential across each individual capacitor is the same and equal to the applied potential.
3. Charge on each capacitor is different and is proportional to capacity of capacitor
   
   $\mathrm{Q} \propto \mathrm{C}$ So
   
   $\mathrm{Q}_{1}=\mathrm{C}_{1} \mathrm{~V}, \mathrm{Q}_{2}=\mathrm{C}_{2} \mathrm{~V}$
   
   $\mathrm{Q}_{3}=\mathrm{C}_{3} \mathrm{~V}$
4. The parallel combination obeys the law of conservation of charge
   
   So $Q=Q_{1}+Q_{2}+Q_{3}$
   
   $=\mathrm{C}_{1} \mathrm{~V}+\mathrm{C}_{2} \mathrm{~V}+\mathrm{C}_{3} \mathrm{~V}$
   
   $=\left(C_{1}+C_{2}+C_{3}\right) V$
   
   equivalent capacitance
   
   $C_{p}=\frac{Q}{V}=C_{1}+C_{2}+C_{3}$



5. The equivalent capacitance may be defined as the capacitance of a single capacitor that would acquire the same total charge Q with the same potential difference V.
6. The equivalent capacitance in parallel is equal to the sum of individual capacitances.
7. The equivalent capacitance is greater than the largest of individual capacitances.
8. The capacitors are connected in parallel (a) to increase the capacitance (b) when larger capacitance is required at low potential.
9. If n identical capacitors are connected in parallel then equivalent parallel capacitance $C_{p}=n C$
10. The total energy stored in parallel combination
    
    $U=\frac{1}{2} C_{p} V^{2}$
    
    $=\frac{1}{2}\left(\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}+\ldots .\right) \mathrm{V}^{2}$
    
    $U=\frac{1}{2} C_{1} V^{2}+\frac{1}{2} C_{2} V^{2}+\ldots$
    
    $=U_{1}+U_{2}$$+U_{3}+\ldots \ldots$
    
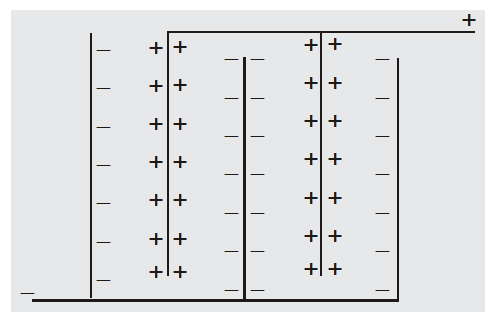
    The total energy stored in parallel combination is equal to the sum of energies stored in individual capacitors.
11. If n plates are arranged as shown they constitute (n–1)capacitors in parallel each of capacitance $\frac{\varepsilon_{0} \mathrm{~A}}{\mathrm{~d}}$
    
    Equivalent capacitance $C_{P}=(n-1) \frac{\varepsilon_{0} A}{d}$

Series Combination

1. Capacitors are said to be connected in series between two points if it is possible to proceed from one point to the other point along only one path. 1
2. Capacitors are said to be in series if the charge on each individual capacitor is the same
3. The potential difference across each capacitor is different and is inversely proportional to its capacitance $V \propto \frac{1}{C}$
   
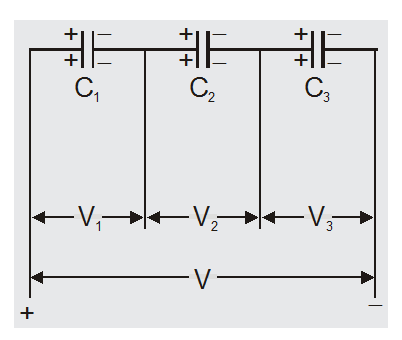
   $\mathrm{V}_{1}=\frac{\mathrm{Q}}{\mathrm{C}_{1}}$
   
   $\mathrm{V}_{2}=\frac{\mathrm{Q}}{\mathrm{C}_{2}}$
   
   and $\quad V_{3}=\frac{Q}{C_{3}}$



4. The series combination obeys the law of conservation of energy
   
   So $\quad V=V_{1}+V_{2}+V_{3}$
   
   $=\frac{Q}{C_{1}}+\frac{Q}{C_{2}}+\frac{Q}{C_{3}}$
   
   $=Q\left(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\right)$
   
   reciprocal of equivalent capacitance
   
   $\frac{1}{\mathrm{C}_{\mathrm{s}}}=\frac{\mathrm{V}}{\mathrm{Q}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}$



5. The equivalent capacitance in series combination is the capacitance of a single capacitor that would become charged with the same charge Q when a potential difference is V.
6. The reciprocal of the equivalent capacitance is equal to the sum of the reciprocal of individual capacitance.
7. The equivalent capacitance is smaller than the smallest of individual capacitances.
8. The capacitors are connected in series (a) to decrease the capacitance (b) to divide large potential differences across many capacitors.
9. In n identical capacitors are connected in series than equivalent series capacitance $C_{s}=\frac{C}{n}$
10. The total energy stored in a series combination $U=\frac{Q^{2}}{2 C s}$
    
    $=\frac{Q^{2}}{2}\left(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\ldots \ldots\right)$
    
    or
    
    $\mathrm{U}=\frac{\mathrm{Q}^{2}}{2 \mathrm{C}_{1}}+\frac{\mathrm{Q}^{2}}{2 \mathrm{C}_{2}}+\frac{\mathrm{Q}^{2}}{2 \mathrm{C}_{3}}+\ldots \ldots$
    
    $=\mathrm{U}_{1}+\mathrm{U}_{2}+\mathrm{U}_{3}+\ldots \ldots$
    
    The total energy stored in series combinations is equal to the sum of energies stored in individual capacitors.
11. If n plates are arranged as shown then they constitute (n–1) capacitors in series each of
    
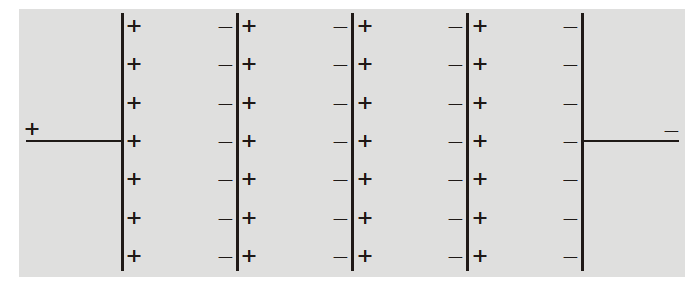
    value $\frac{\varepsilon_{0} A}{d}$
    
    so
    
    $C_{S}=\frac{\varepsilon_{0} A}{(n-1) d}$

so, that's all from this article. I hope you get the idea about the combination of capacitors. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of Electrostatics Class 12. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.