Start Prep From 0 & Get IIT Bombay with Most Powerful JEE Dropper Course
Enroll Now!

Complex Number - JEE Main Previous Year Question with Solutions

Complex Number questions appear in JEE Main every year, typically 1–2 questions per paper. Key topics include modulus-argument properties, unimodular numbers, cube roots of unity, and locus problems. Questions from 2009 to 2017 (AIEEE/JEE Main) follow predictable patterns that can be mastered with targeted practice on previous year papers.
eSaral Updated on:
Complex Number - JEE Main Previous Year Question with Solutions

Home > JEE Main Previous Year Questions > Complex Number JEE Main Previous Year Questions with Solutions

🚀 Checkout eSaral Courses

JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas. Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc. eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects. Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more. Download eSaral app for free study material and video tutorials.

Q. If $\left|Z-\frac{4}{Z}\right|=2,$ then the maximum value of $|Z|$ is equal to :-. (1) 2 (2) $2+\sqrt{2}$ (3) $\sqrt{3}+1$ (4) $\sqrt{5}+1$ [AIEEE -2009]
Ans. (4) $\left|z-\frac{4}{z}\right| \geq|z|-\left|\frac{4}{z}\right|$ $2 \geq|z|-\frac{4}{|z|}$ $2|z| \geq|z|^{2}-4$ $|z|^{2}-2|z|-4 \leq 0$ $|z| \leq \sqrt{5}+1$
Q. The number of complex numbers z such that $|z-1|=|z+1|=|z-i|$ equals :- (1) 0 (2)1 (3) 2 (4) $\infty$ [AIEEE -2010]
Ans. (2) z is the circumcentre (0, 0) of triangle ABC so their exist only one complex number.
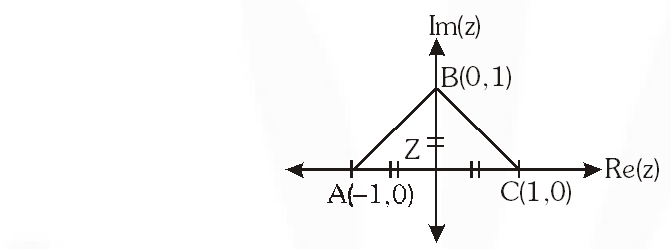
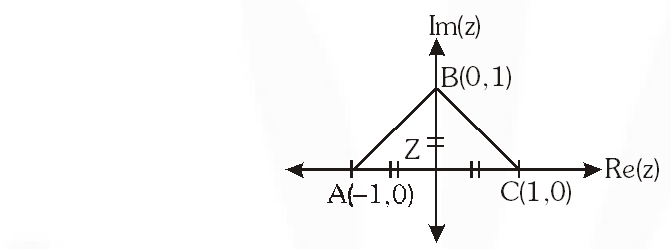
Q. Let $\alpha, \beta$ be real and $z$ be a complex number. If $z^{2}+\alpha z+\beta=0$ has two distinct roots on the line $\operatorname{Re} z=1,$ then it is necessary that :- (1) $|\beta|=1$ (2) $\beta \in(1, \infty)$ (3) $\beta \in(0,1)$ (4) $\beta \in(-1,0)$ [AIEEE -2011]
Ans. (2) Let $z^{2}+\alpha z+\beta=0$ has $\left(1+i y_{1}\right)$ and $\left(1+i y_{2}\right)$ so $z_{1} z_{2}=\beta$ $\left(1+i y_{1}\right)\left(1+i y_{2}\right)=\beta$ $\beta=1-\mathrm{y}_{1} \mathrm{y}_{2}+\mathrm{i}\left(\mathrm{y}_{1}+\mathrm{y}_{2}\right)(\because \beta \text { is purely real })$ here $\mathrm{y}_{1}+\mathrm{y}_{2}=0$ $\mathrm{y}_{1}=-\mathrm{y}_{2}$ $\beta=1-\mathrm{y}_{1} \mathrm{y}_{2}$ $\beta=1+\mathrm{y}_{1}^{2}$ $\beta>1$ $\Rightarrow \beta \in(1, \infty)$
Q. If $\omega(\neq 1)$ is a cube root of unity, and $(1+\omega)^{7}=\mathrm{A}+\mathrm{B} \omega .$ Then $(\mathrm{A}, \mathrm{B})$ equals :- (1) (1, 0)        (2) (–1, 1)       (3) (0, 1)          (4) (1, 1) [AIEEE -2011]
Ans. (4) $(1+\omega)^{7}=\mathrm{A}+\mathrm{B} \omega$ $\left(-\omega^{2}\right)^{7}=\mathrm{A}+\mathrm{B} \omega$ $-\omega^{2}=\mathrm{A}+\mathrm{B} \omega$ $1+\omega=\mathrm{A}+\mathrm{B} \omega$ $\mathrm{A}=1$ $\mathrm{B}=1$ (1, 1)
Q. If $z \neq 1$ and $\frac{z^{2}}{z-1}$ is real, then the point represented by the complex number $z$ lies : (1) on the imaginary axis. (2) either on the real axis or on a circle passing through the origin. (3) on a circle with centre at the origin. (4) either on the real axis or on a circle not passing through the origin. [AIEEE -2012]
Ans. (2) $\frac{z^{2}}{z-1}$ is purely real where $(Z \neq 1)$
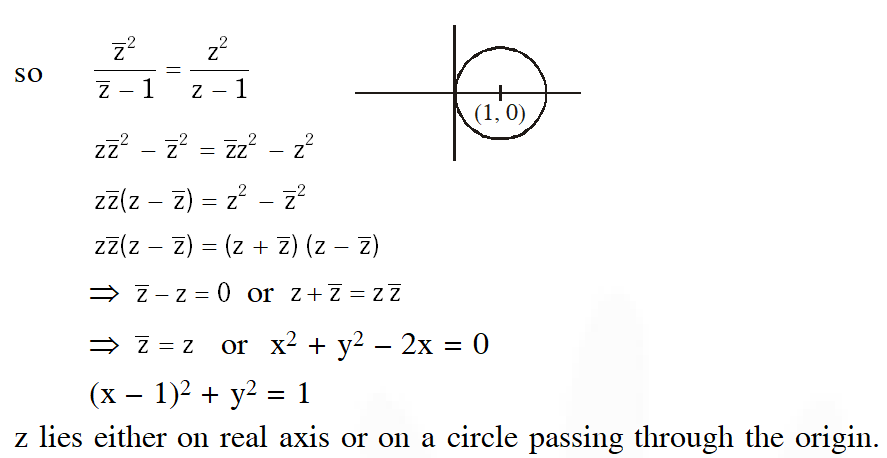
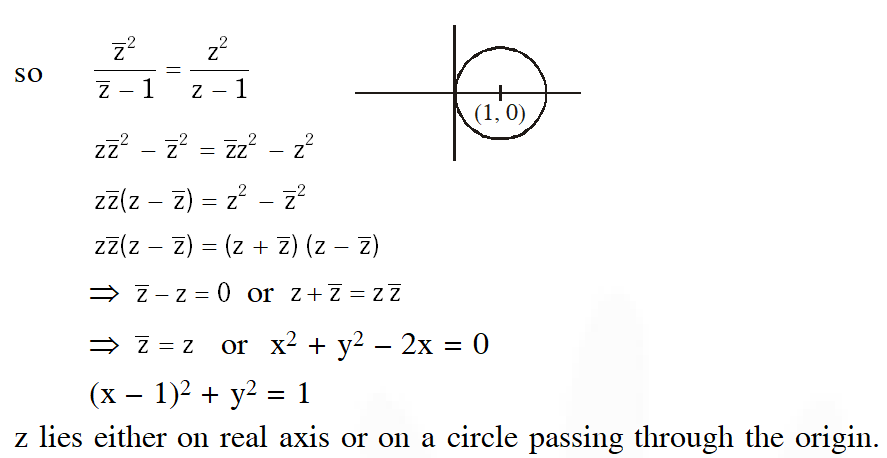
Q. If $z$ is a complex number of unit modulus and argument $\theta,$ then $\arg \left(\frac{1+z}{1+\bar{z}}\right)$ equals (1) $-\theta$ (2) $\frac{\pi}{2}-\theta$ (3) $\theta$ (4) $\pi-\theta$ [JEE (Main)-2013]
Ans. (3) $\bar{z}=\frac{1}{z} \Rightarrow \arg \left(\frac{1+z}{1+\frac{1}{z}}\right) \quad \Rightarrow \operatorname{argz} \Rightarrow \theta$
Q. If $\mathrm{z}$ is a complex number such that $|\mathrm{z}| \geq 2,$ then the minimum value of $\left|\mathrm{z}+\frac{1}{2}\right|:$ (1) is equal to $\frac{5}{2}$ (2) lies in the interval (1, 2) (3) is strictly greater than $\frac{5}{2}$ (4) is strictly greater than $\frac{3}{2}$ but less than [JEE (Main)-2014]
Ans. (2) $\left|z+\frac{1}{2}\right| \geq|| z\left|-\frac{1}{2}\right|$ Min. value of $\left|z+\frac{1}{2}\right|$ occurs at $|z|=2$ $\because|z| \geq 2$ $\therefore\left|z+\frac{1}{2}\right|_{\text {min }}=\left|2-\frac{1}{2}\right|=\frac{3}{2}$
Q. A complex number $z$ is said to be unimodular if $|z|=1 .$ Suppose $z_{1}$ and $z_{2}$ are complex numbers such that $\frac{z_{1}-2 z_{2}}{2-z_{1} \bar{z}_{2}}$ is unimodular and $z_{2}$ is not unimodular. Then the point $z_{1}$ lies on a : (1) circle of radius 2 (2) circle of radius $\sqrt{2}$ (3) straight line parallel to x-axis (4) straight line parallel to y-axis [JEE (Main)-2015]
Ans. (1) $\frac{\left|z_{1}-2 z_{2}\right|}{\left|2-z_{1} \bar{z}_{2}\right|}=1$ $\Rightarrow \quad\left|z_{1}-2 z_{2}\right|^{2}=\left|2-z_{1} \bar{z}_{2}\right|^{2}$ $\Rightarrow\left(z_{1}-2 z_{2}\right)\left(\bar{z}_{1}-2 \bar{z}_{2}\right)=\left(2-z_{1} \bar{z}_{2}\right)\left(2-\bar{z}_{1} z_{2}\right)$ $\Rightarrow\left|z_{1}\right|^{2}+4\left|z_{2}\right|^{2}-4-\left|z_{1}\right|^{2}\left|z_{2}\right|^{2}=0$ $\Rightarrow 4\left(\left|z_{2}\right|^{2}-1\right)-\left|z_{1}\right|^{2}\left(\left|z_{2}\right|^{2}-1\right)=0$ $\Rightarrow\left|z_{1}\right|^{2}-4=0 \Rightarrow\left|z_{1}\right|=2$ is a circle of radius 2 and centre at origin. Alter $\frac{\left|z_{1}-2 z_{2}\right|}{\left|2-z_{1} \bar{z}_{2}\right|}=1$ $\left(z_{1}-2 z_{2}\right)\left(\bar{z}_{1}-2 \bar{z}_{2}\right)=\left(2-z_{1} \bar{z}_{2}\right)\left(2-\bar{z}_{1} z_{2}\right)$ $\left|z_{1}\right|^{2}-2 z_{1} \bar{z}_{2}-2 z_{2} \bar{z}_{1}+4\left|z_{2}\right|^{2}$ $=4-2 z_{1} \bar{z}_{2}-2 z_{1} \bar{z}_{2}+\left|z_{1}\right|^{2}\left|z_{2}\right|^{2}$ $\left|z_{2}\right|^{2}\left(1-\left|z_{2}\right|^{2}\right)-4\left(1-\left|z_{2}\right|^{2}\right)=0$ $\left.\Rightarrow\left|z_{1}\right|=2 \quad \text { (as }\left|z_{2}\right| \neq 1\right)$ $\Rightarrow$ which is circle of radius 2
Q. A value of $\theta$ for which $\frac{2+3 \text { isin } \theta}{1-2 i \sin \theta}$ is purely imaginary, is : (1) $\sin ^{-1}\left(\frac{1}{\sqrt{3}}\right)$ (2) $\frac{\pi}{3}$ (3) $\frac{\pi}{6}$ (4) $\sin ^{-1}\left(\frac{\sqrt{3}}{4}\right)$ [JEE (Main)-2016]
Ans. (1) $\begin{aligned} \mathrm{Z}=& \frac{2+3 \mathrm{i} \sin \theta}{1-2 \mathrm{i} \sin \theta} \\ \Rightarrow \mathrm{Z} &=\frac{(2+3 \mathrm{i} \sin \theta)(1+2 \mathrm{i} \sin \theta)}{1+4 \sin ^{2} \theta} \\ &=\frac{\left(2-6 \sin ^{2} \theta\right)+7 \mathrm{i} \sin \theta}{1+4 \sin ^{2} \theta} \end{aligned}$ for purely imaginary $Z, \operatorname{Re}(Z)=0$ $\Rightarrow 2-6 \sin ^{2} \theta=0 \Rightarrow \sin \theta=\pm \frac{1}{\sqrt{3}}$ $\Rightarrow \theta=\pm \sin ^{-1}\left(\frac{1}{\sqrt{3}}\right)$
Q. Let $\omega$ be a complex number such that $2 \omega+1=z$ where $z=\sqrt{-3} .$ If $\left|\begin{array}{ccc}{1} & {1} & {1} \\ {1} & {-\omega^{2}-1} & {\omega^{2}} \\ {1} & {\omega^{2}} & {\omega^{7}}\end{array}\right|=3 \mathrm{k},$ then $\mathrm{k}$ is equal to : (1) 1             (2) –z           (3) z             (4) –1 [JEE (Main)-2017]
Ans. (2) Here $\omega$ is complex cube root of unity $\quad \mathrm{R}_{1} \rightarrow \mathrm{R}_{1}+\mathrm{R}_{2}+\mathrm{R}_{3}$ $=\left|\begin{array}{ccc}{3} & {0} & {0} \\ {1} & {-\omega^{2}-1} & {\omega^{2}} \\ {1} & {\omega^{2}} & {\omega}\end{array}\right|=3(-1-\omega-\omega)=-3 \mathrm{z} \Rightarrow \mathrm{k}=-\mathrm{z}$

Frequently Asked Questions

Find answers to common questions.

Is NCERT sufficient for Complex Numbers in JEE Main?

NCERT builds the necessary foundation — definitions, basic operations, modulus, and argument. However, JEE Main questions require a higher level of application. After completing NCERT, students must practise PYQs and topic-specific problem sets. You can start with NCERT Solutions Class 11 Maths and then move to JEE-level drill problems.

What are the most important subtopics in Complex Numbers for JEE Main?

The most frequently tested subtopics are: modulus and its inequalities, argument and conjugate properties, cube roots of unity (ω), unimodular numbers, and geometric loci in the Argand plane. Together, these five areas account for roughly 85% of all JEE Main complex number questions since 2009

How many questions from Complex Numbers appear in JEE Main each year?

JEE Main typically includes 1 to 2 questions from Complex Numbers per paper. With two sessions per year, a serious aspirant should expect 2–4 questions annually. Given the consistency of the topic, solving all PYQs from 2009 onwards gives strong predictive value for new questions.

How much time should I spend on Complex Numbers during JEE Main preparation?

Allocate roughly 10–12 hours of focused study to Complex Numbers: 3–4 hours for theory and NCERT, 4–5 hours for solving 40–50 PYQs with solutions, and 2–3 hours for timed mock practice. Because the question patterns repeat, this is one of the highest-ROI topics in JEE Main Maths.

How should I approach "purely real" or "purely imaginary" condition questions?

Write z = x + iy, then simplify the given expression by multiplying numerator and denominator by the conjugate. For a purely real expression, set the imaginary part equal to zero. For purely imaginary, set the real part equal to zero. This direct method works for 90% of such questions and avoids common errors.

What is a unimodular complex number?

A complex number z is called unimodular when its modulus equals 1, i.e., |z| = 1. This means z lies on the unit circle in the Argand plane. Unimodular numbers appear frequently in JEE Main locus questions because the condition |z| = 1 allows elegant algebraic simplifications, particularly when z̄ = 1/z

Leave a comment

Comments

fnfOzvSR
March 30, 2026, 5:55 a.m.
1
fnfOzvSR
March 30, 2026, 5:55 a.m.
1
fnfOzvSR
March 30, 2026, 5:53 a.m.
1
fnfOzvSR
March 30, 2026, 5:53 a.m.
1
jayesh
Sept. 12, 2025, 6:35 a.m.
only call in whatsApp
jayesh
Sept. 12, 2025, 6:35 a.m.
MB Hight hostel near city park
jayesh
Sept. 12, 2025, 6:35 a.m.
sir i am your big fan and study at Allen please give me PYQ sheet
jayesh
Sept. 12, 2025, 6:35 a.m.
8999547906
Siddharth
July 21, 2024, 6:35 a.m.
Ooo
Siddharth
July 21, 2024, 6:35 a.m.
Thnx
.
March 6, 2021, 1:12 p.m.
.
rajarshi
Feb. 25, 2021, 10:34 a.m.
sir send some more question from previous year jee main
MR.BENIWAL
Dec. 23, 2020, 12:22 a.m.
Thanks
sdsdfsdf
Dec. 15, 2020, 5:17 p.m.
sdfsdfsdf
Kritika
Nov. 11, 2020, 8:28 p.m.
Please provide more question for jee mains & jee advanced level
Hahahaha
Oct. 22, 2020, 9:08 p.m.
Hahahaha
Kpy
Oct. 14, 2020, 7:59 p.m.
Nice
Ashok
Sept. 14, 2020, 6:24 p.m.
Thanks you
Neelll
Sept. 11, 2020, 10:17 p.m.
Goood one
N.H arika lakshmi sai
Aug. 28, 2020, 6:14 p.m.
Sir send some more questions regarding complex numbers
jahnavi
Aug. 27, 2020, 8:33 p.m.
thank u but plz update the questions till2020
Manoj
Aug. 25, 2020, 9:30 a.m.
Thanks you sir
Bindu
Aug. 6, 2020, 12:04 p.m.
Thanku so much
Bharat
Aug. 4, 2020, 9:48 p.m.
Excellent approach...
ganesh
July 25, 2020, 9:24 p.m.
OK
ganesh
July 25, 2020, 9:23 p.m.
good
Sri harshitha katla
June 20, 2020, 10:47 a.m.
Update all questions of jee till 2020
Ruhi
June 20, 2020, 10:46 a.m.
Good
patel saurabh
June 11, 2020, 2:41 p.m.
please upload all question till 2020
Adarsh Yadav
April 19, 2020, 2:34 p.m.
Best questions
Sabari
April 10, 2020, 5:01 p.m.
Thank you
None

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material