JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Given that for each a $\in(0,1)$, $\lim _{\mathrm{h} \rightarrow 0^{+}} \int_{\mathrm{h}}^{1-\mathrm{h}} \mathrm{t}^{-\mathrm{a}}(1-\mathrm{t})^{\mathrm{a}-1}$ $\mathrm{dt}$ exists. Let this limit be g(a). In addition,
it is given that the function g(a) is differentiable on (0,1).
Let $\mathrm{F}: \mathbb{U} \rightarrow \square$ be a thrice differentiable function. Suppose that $\mathrm{F}(1)=0, \mathrm{F}(3)=-4 \mathrm{F}^{\prime}(\mathrm{x})<$ 0 for all $\mathrm{x} \in(1 / 2,3) .$ Let $f(\mathrm{x})=\mathrm{xF}(\mathrm{x})$ for all $\mathrm{x} \in \mathbb{D}$.
Q. Let ƒ be a non-negative function defined on the interval $[0,1] .$ If $\int_{0}^{x} \sqrt{1-\left(f^{\prime}(t)\right)^{2}} d t=\int_{0}^{x} f(t) d t$ $0 \leq \mathrm{x} \leq 1,$ and $f(0)=0,$ then $-$
(A) $f\left(\frac{1}{2}\right)<\frac{1}{2}$ and $f\left(\frac{1}{3}\right)>\frac{1}{3}$
(B) $f\left(\frac{1}{2}\right)>\frac{1}{2}$ and $f\left(\frac{1}{3}\right)>\frac{1}{3}$
(C) $f\left(\frac{1}{2}\right)<\frac{1}{2}$ and $f\left(\frac{1}{3}\right)<\frac{1}{3}$
(D) $f\left(\frac{1}{2}\right)>\frac{1}{2}$ and $f\left(\frac{1}{3}\right)<\frac{1}{3}$
[JEE 2009, 3]
Ans. (C)
$\int_{0}^{x} \sqrt{1-\left(f^{\prime}(t)\right)^{2}} \mathrm{d} t=\int_{0}^{x} f(t) d t, 0 \leq x \leq 1$
differentiating both the sides & squreing
$\Rightarrow 1-\left(f^{\prime}(\mathrm{x})\right)^{2}=f^{2}(\mathrm{x})$
$\Rightarrow \frac{f^{\prime}(x)}{\sqrt{1-f^{2}(x)}}=1$
$\Rightarrow \sin ^{-1} f(\mathrm{x})=\mathrm{x}+\mathrm{c}$
$f(0)=0$
$\Rightarrow f(\mathrm{x})=\sin \mathrm{x}$
$\Rightarrow \because \sin \mathrm{x} \leq \mathrm{x}$ for $\mathrm{x} \in[0,1]$
$\Rightarrow f\left(\frac{1}{2}\right)<\frac{1}{2}$ and $f\left(\frac{1}{3}\right)<\frac{1}{3}$
Q. If $\mathrm{I}_{\mathrm{n}}=\int_{-\pi}^{\pi} \frac{\sin \mathrm{nx}}{\left(1+\pi^{\mathrm{x}}\right) \sin \mathrm{x}} \mathrm{d} \mathrm{x}, \mathrm{n}=0,1,2, \ldots, \mathrm{then}-$
(A) $\mathrm{I}_{\mathrm{n}}=\mathrm{I}_{\mathrm{n}+2}$
(B) $\sum_{\mathrm{m}=1}^{10} \mathrm{I}_{2 \mathrm{m}+1}=10 \pi$
(C) $\sum_{\mathrm{m}=1}^{10} \mathrm{I}_{2 \mathrm{m}}=0$
(D) $\mathrm{I}_{\mathrm{n}}=\mathrm{I}_{\mathrm{n}+1}$
[JEE 2009, 4]
Ans. (A,B,D)
$\mathrm{I}_{\mathrm{n}}=\int_{-\pi}^{\pi} \frac{\sin \mathrm{nx}}{\left(1+\pi^{\mathrm{x}}\right) \sin \mathrm{x}} \mathrm{dx}$
$\mathrm{I}_{\mathrm{n}}=\int_{-\pi}^{\pi} \frac{\pi^{\mathrm{x}} \sin \mathrm{nx}}{\left(1+\pi^{\mathrm{x}}\right) \sin \mathrm{x}} \mathrm{dx}$
$2 \mathrm{I}_{\mathrm{n}}=\int_{-\pi}^{\pi} \frac{\sin \mathrm{nx}}{\sin \mathrm{x}} \mathrm{dx}$ ..(i)
$2 \mathrm{I}_{\mathrm{n}+2}=\int_{-\pi}^{\pi} \frac{\sin (\mathrm{n}+2) \mathrm{x}}{\sin \mathrm{x}} \mathrm{dx} \quad \ldots(\mathrm{i})$
(ii) – (i)
$\Rightarrow 2\left(\ln _{+2}-\mathrm{I}_{\mathrm{n}}\right)=\int_{-\pi}^{\pi} \cos (\mathrm{n}+1) \mathrm{x}=0$
$\Rightarrow \quad \mathrm{I}_{\mathrm{n}+2}=\mathrm{I}_{\mathrm{n}}$
$\sum_{m=1}^{10} \mathrm{I}_{2 \mathrm{m}}=10 \sum_{\mathrm{m}=1}^{10} \mathrm{I}_{2}=\frac{10}{2} \int_{-\pi}^{\pi} \frac{\sin 2 \mathrm{x}}{\sin \mathrm{x}} \mathrm{d} \mathrm{x}=0$
Put n = 1 in equation (i)
$2 \mathrm{I}_{1}=\int_{-\pi}^{\pi} \frac{\sin \mathrm{x} \mathrm{d} \mathrm{x}}{\sin \mathrm{x}}=2 \pi$
$\mathrm{I}_{1}=\pi$
$\sum_{m=1}^{10} I_{2 m+1}=10 \pi$
Q. Let $\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}$ be a continuous function which satisfies $\mathrm{f}(\mathrm{x})=\int_{0}^{\mathrm{x}} \mathrm{f}(\mathrm{t}) \mathrm{d} \mathrm{t}$ Then the value of f(ln 5) is........
[JEE 2009, 4]
Ans. 0
$\mathrm{f}(\mathrm{x})=\int_{0}^{\mathrm{x}} \mathrm{f}(\mathrm{t}) \mathrm{dt}$
$\mathrm{f}^{\mathrm{l}}(\mathrm{x})=\mathrm{f}(\mathrm{x})$
$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{y}$
$\Rightarrow \int \frac{d y}{y}=\int d x$
$\Rightarrow \ln y=x+c$
$\Rightarrow y=e^{x+c}$
$\Rightarrow y=0$
$\left(\begin{array}{c}{\text { at } x=0, y=0} \\ {c \rightarrow-\infty}\end{array}\right)$
$f(x)=0$
$f(\ell n 5)=0$
Q. The value of $\lim _{x \rightarrow 0} \frac{1}{x^{3}} \int_{0}^{x} \frac{t \ell n(1+t)}{t^{4}+4} d t$ is
(A) 0
(B) $\frac{1}{12}$
(C) $\frac{1}{24}$
(D) $\frac{1}{64}$
[JEE 2010, 3 (–1)]
Ans. (B)
Applying L-Hospital rule,
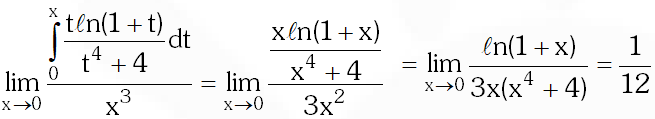
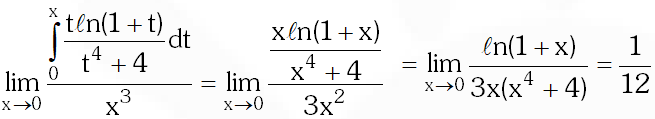
Q. The value(s) of $\int_{0}^{1} \frac{\mathrm{x}^{4}(1-\mathrm{x})^{4}}{1+\mathrm{x}^{2}} \mathrm{dx}$ is (are)
(A) $\frac{22}{7}-\pi$
(B) $\frac{2}{105}$
(C) 0
(D) $\frac{71}{15}-\frac{3 \pi}{2}$
[JEE 2010, 3]
Ans. (A)
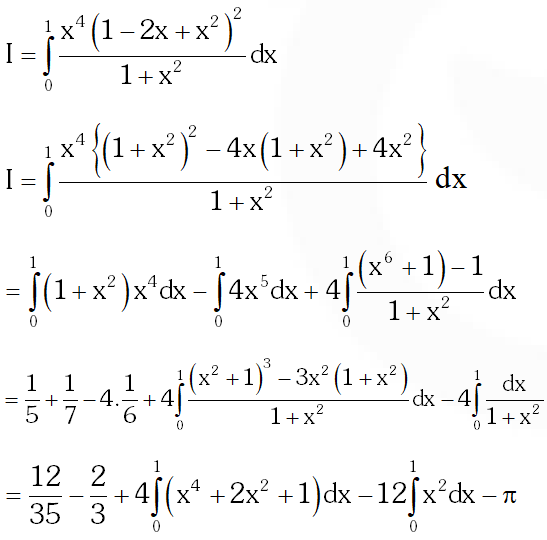
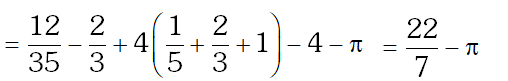
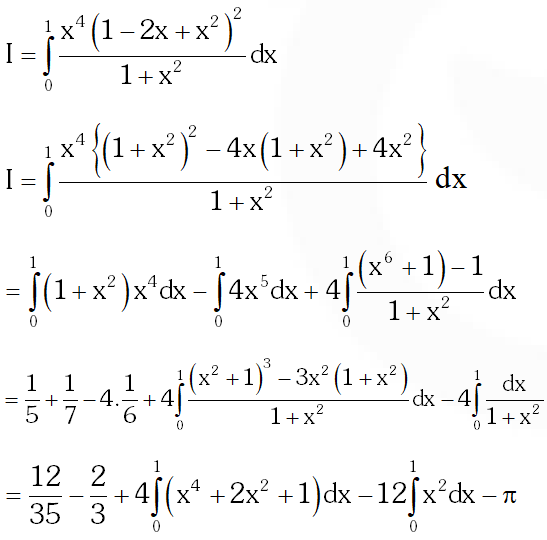
Q. Let $f$ be a real-valued function defined on the interval $(-1,1)$ such that
$e^{-x} f(x)=2+\int_{0}^{x} \sqrt{t^{4}+1} d t,$ for all $x \in(-1,1),$ and let $f^{-1}$ be the inverse function of $f$ Then $\left(f^{-1}\right)^{\prime}(2)$ is equal to-
(A) 1
(B) $\frac{1}{3}$
(C) $\frac{1}{2}$
(D) $\frac{1}{\mathrm{e}}$
[JEE2010, 5 (–2)]
Ans. (B)
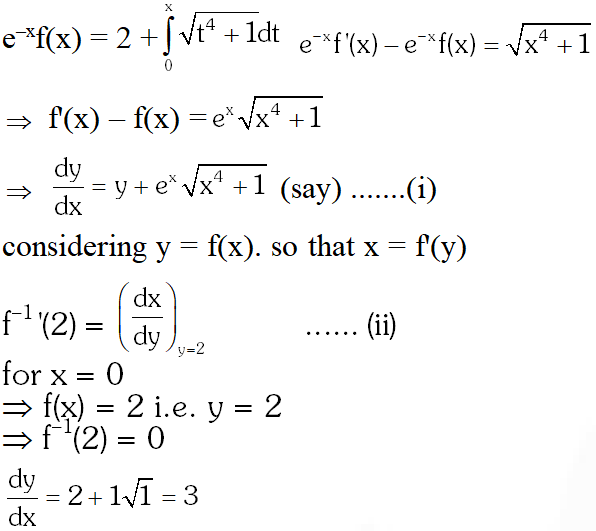 from $(2), f^{-1}(2)=\frac{1}{3}$
from $(2), f^{-1}(2)=\frac{1}{3}$
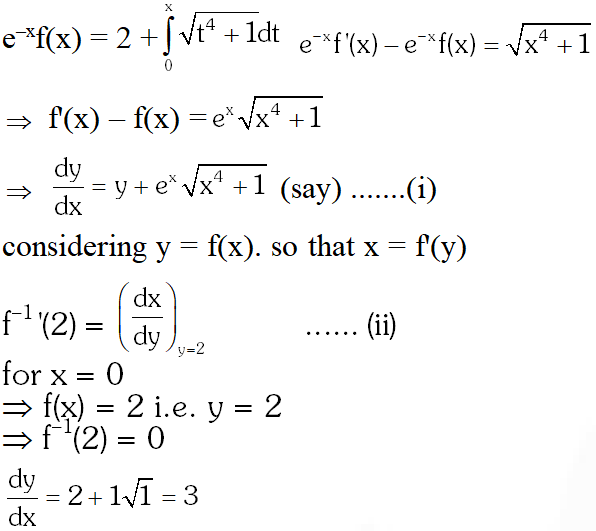 from $(2), f^{-1}(2)=\frac{1}{3}$
from $(2), f^{-1}(2)=\frac{1}{3}$
Q. For any real number x, let [x] denote the largest integer less than or equal to x. Let f be a real valued function defined on the interval [–10, 10] by $\mathrm{f}(\mathrm{x})=\left\{\begin{aligned} \mathrm{x}-[\mathrm{x}] & \text { if }[\mathrm{x}] \text { is odd } \\ 1+[\mathrm{x}]-\mathrm{x} & \text { if }[\mathrm{x}] \text { is even } \end{aligned}\right.$ Then the value of $\frac{\pi^{2}}{10} \int_{-10}^{10} \mathrm{f}(\mathrm{x}) \cos \pi \mathrm{x} \mathrm{d} \mathrm{x}$ is
[JEE 2010, 3]
Ans. 4
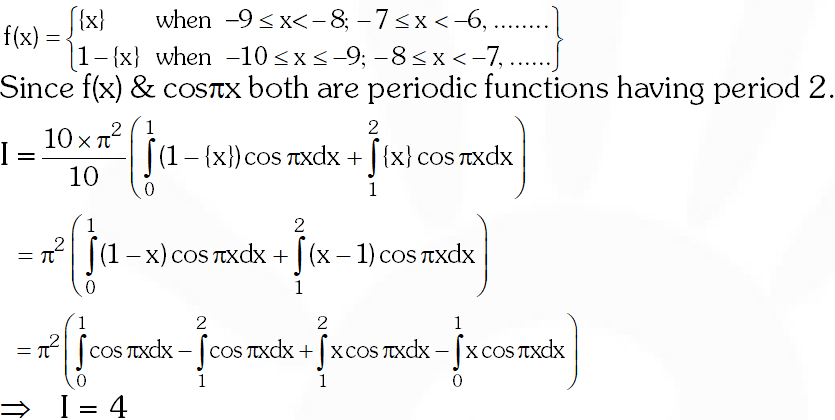
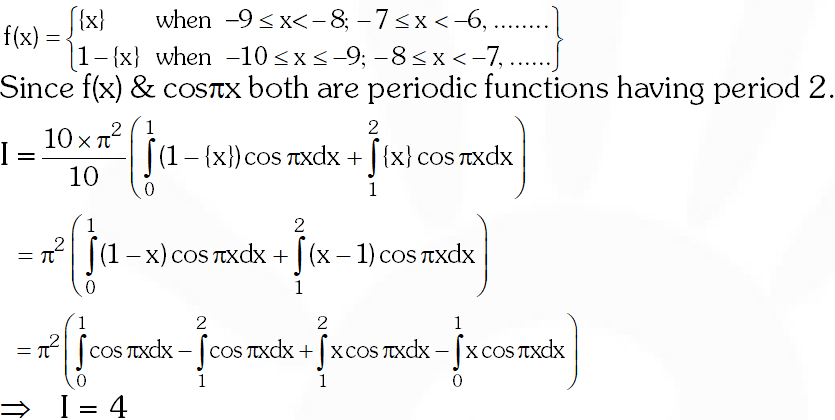
Q. The value of $\int_{\sqrt{\mathrm{in} 2}}^{\sqrt{\mathrm{n} 3}} \frac{\mathrm{x} \sin \mathrm{x}^{2}}{\sin \mathrm{x}^{2}+\sin \left(\mathrm{ln} 6-\mathrm{x}^{2}\right)} \mathrm{dx}$ is
(A) $\frac{1}{4} \ln \frac{3}{2}$
(B) $\frac{1}{2} \ln \frac{3}{2}$
(C) $\ln \frac{3}{2}$
(D) $\frac{1}{6} \ln \frac{3}{2}$
[JEE 2011, 3 (–1)]
Ans. (A)
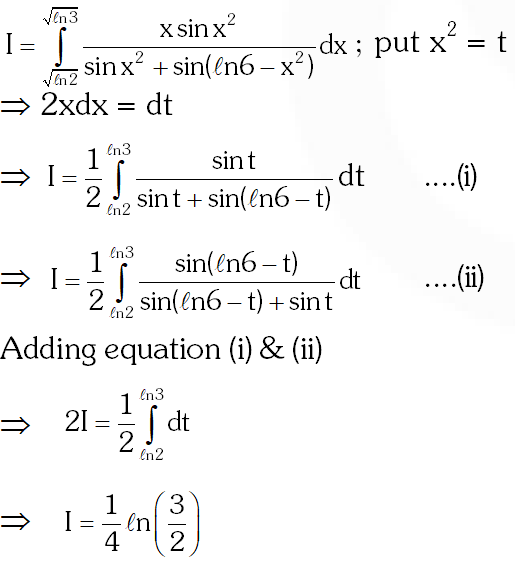
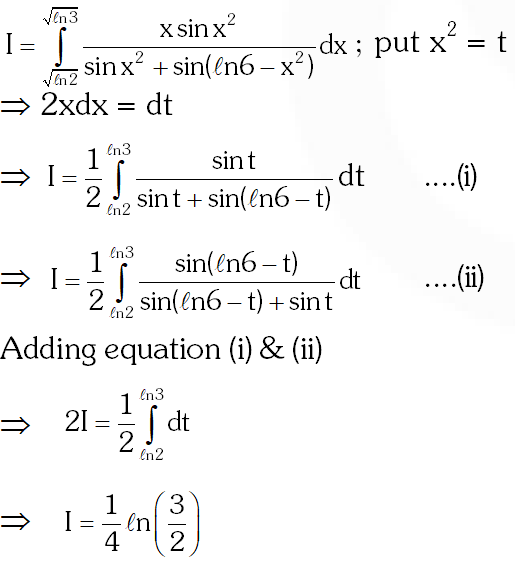
Q. Let $S$ be the area of the region enclosed by $y=e^{-x^{2}}, y=0, x=0,$ and $x=1 .$ Then
(A) $\mathrm{S} \geq \frac{1}{\mathrm{e}}$
(B) $\mathrm{S} \geq 1-\frac{1}{\mathrm{e}}$
(C) $S \leq \frac{1}{4}\left(1+\frac{1}{\sqrt{\mathrm{e}}}\right)$
(D) $S \leq \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{\mathrm{e}}}\left(1-\frac{1}{\sqrt{2}}\right)$
[JEE 2012, 4M]
Ans. (A,B,D)
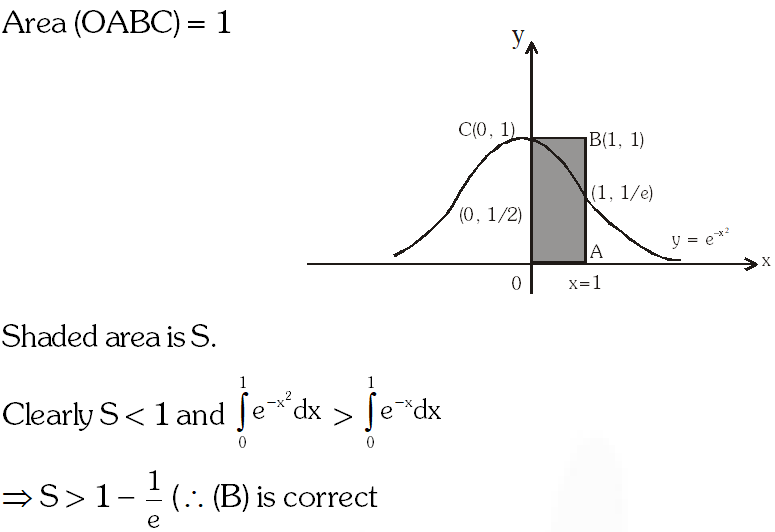
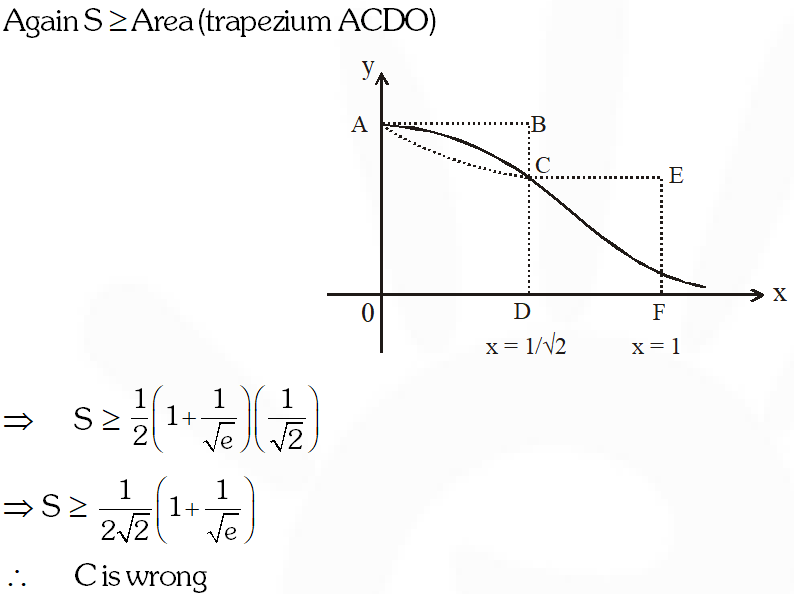
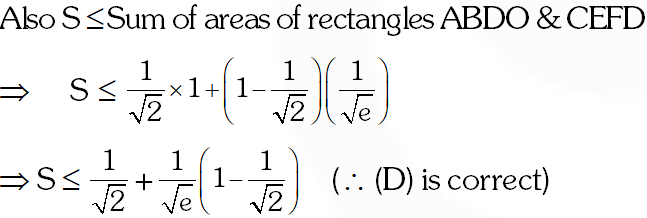
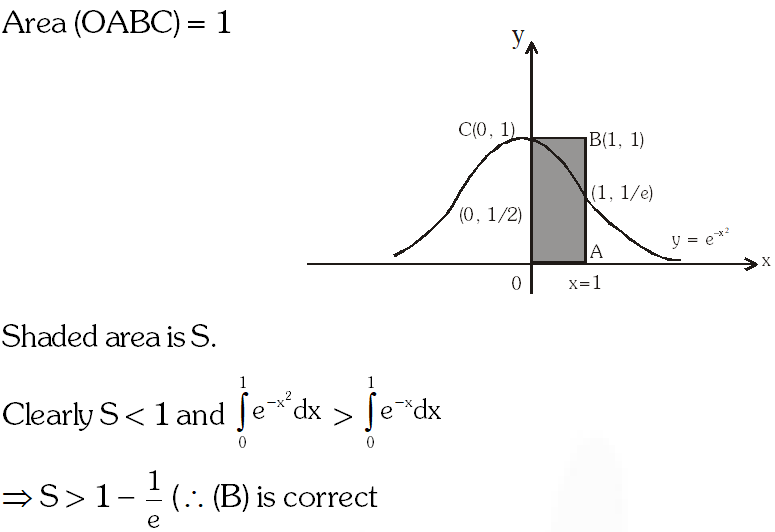
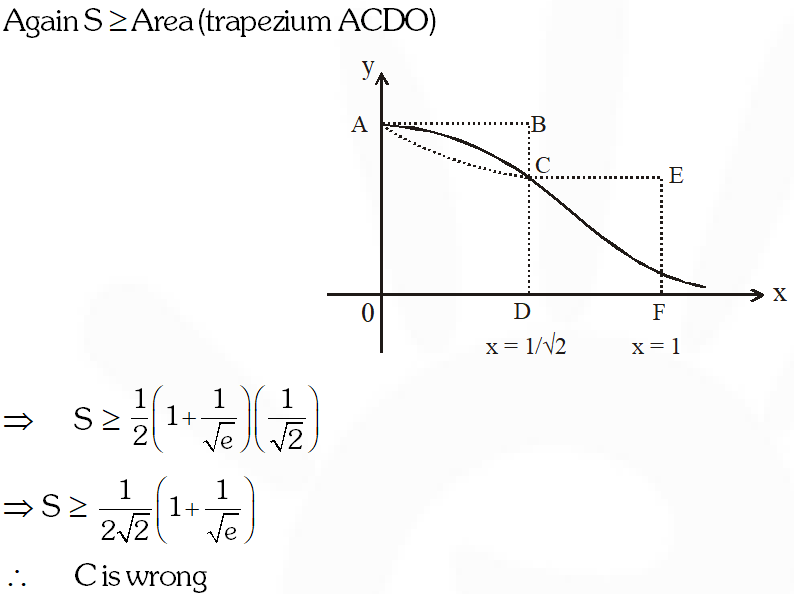
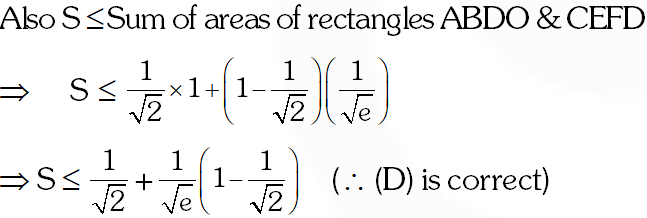
Q. The value of the integral $\int_{-\pi / 2}^{\pi / 2}\left(\mathrm{x}^{2}+\ln \frac{\pi+\mathrm{x}}{\pi-\mathrm{x}}\right) \cos \mathrm{xd} \mathrm{x}$ is
(A) 0
(B) $\frac{\pi^{2}}{2}-4$
(C) $\frac{\pi^{2}}{2}+4$
(D) $\frac{\pi^{2}}{2}$c
[JEE 2012, 3M, –1M]
Ans. (B)
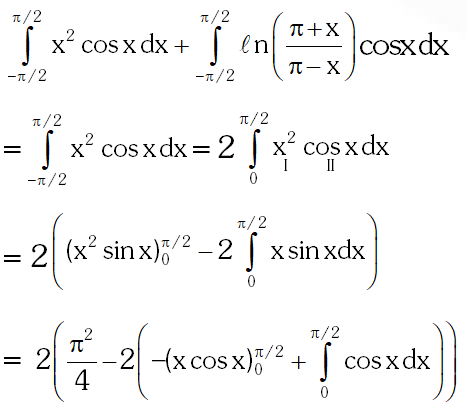
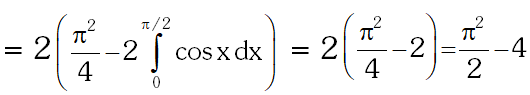
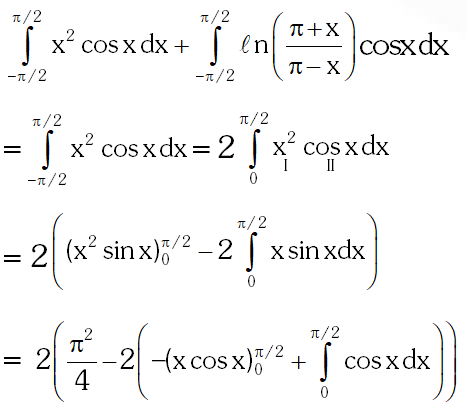
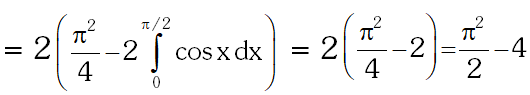
Q. For a $\in \mathrm{R}$ (the set of all real numbers), a\neq-1.
$\lim _{n \rightarrow \infty} \frac{\left(1^{a}+2^{a}+\ldots \ldots+n^{a}\right)}{(n+1)^{a-1}[(n a+1)+(n a+2)+\ldots \ldots+(n a+n)]}=\frac{1}{60}$ Then $a=$
(A) 5 (B) 7 (C) $\frac{-15}{2}$ (D) $\frac{-17}{2}$
[JEE(Advanced) 2013, 3, (–1)]
Ans. (B)
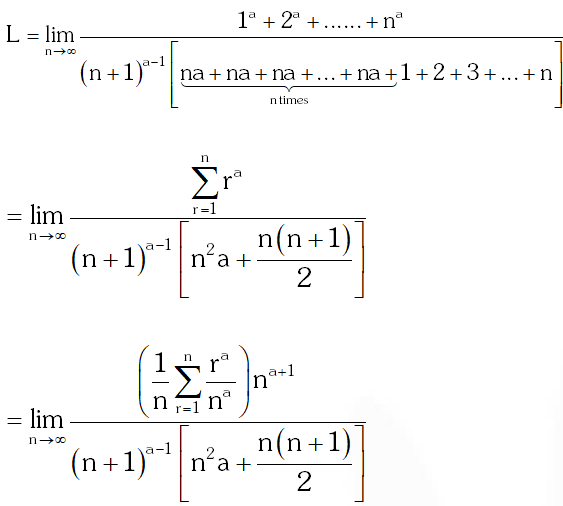
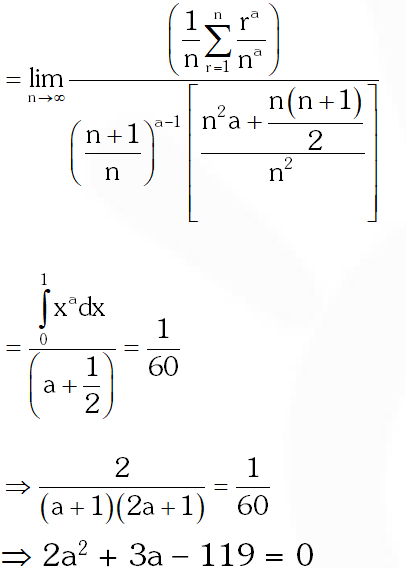
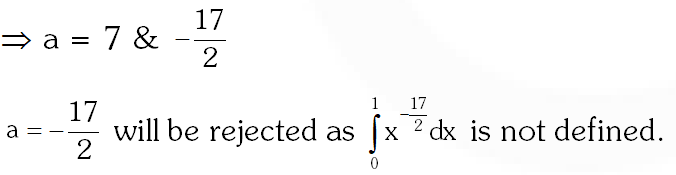
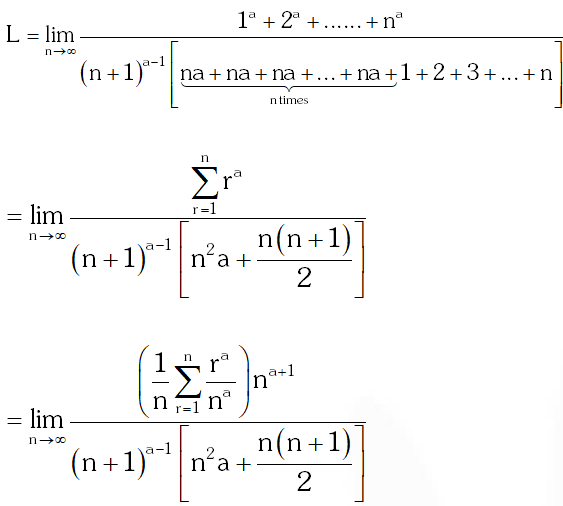
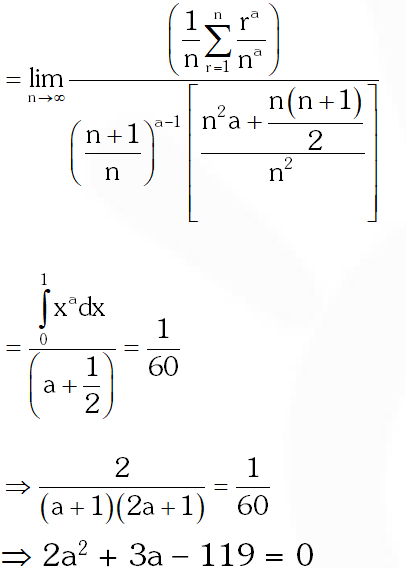
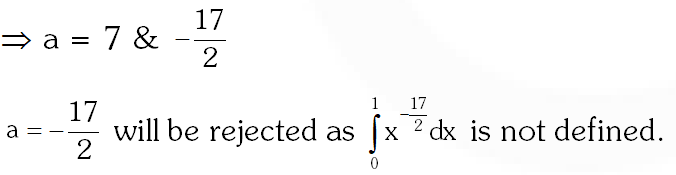
Q. Let $f:[\mathrm{a}, \mathrm{b}] \rightarrow[1, \infty)$ be a continuous function and let $\mathrm{g}: \square \rightarrow \square$ be defined as
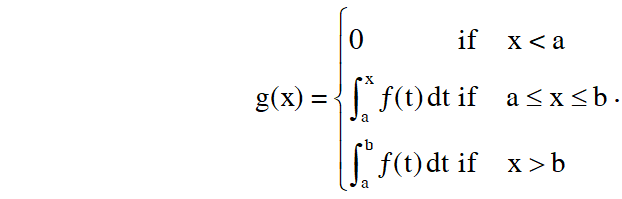 Then
(A) g(x) is continuous but not differentiable at a
(B) g(x) is differentiable on
(C) g(x) is continuous but not differentiable at b
(D) g(x) is continuous and differentiable at either a or b but not both.
[JEE(Advanced)-2014, 3]
Then
(A) g(x) is continuous but not differentiable at a
(B) g(x) is differentiable on
(C) g(x) is continuous but not differentiable at b
(D) g(x) is continuous and differentiable at either a or b but not both.
[JEE(Advanced)-2014, 3]
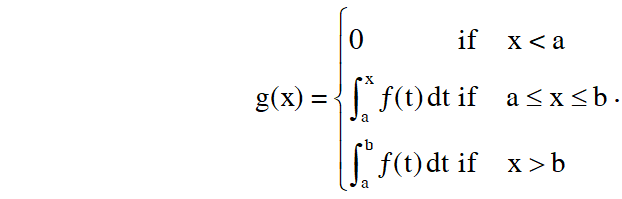 Then
(A) g(x) is continuous but not differentiable at a
(B) g(x) is differentiable on
(C) g(x) is continuous but not differentiable at b
(D) g(x) is continuous and differentiable at either a or b but not both.
[JEE(Advanced)-2014, 3]
Then
(A) g(x) is continuous but not differentiable at a
(B) g(x) is differentiable on
(C) g(x) is continuous but not differentiable at b
(D) g(x) is continuous and differentiable at either a or b but not both.
[JEE(Advanced)-2014, 3]
Ans. (A,C)
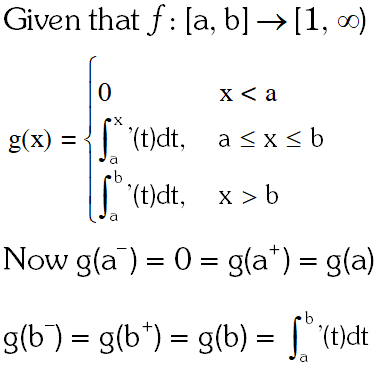
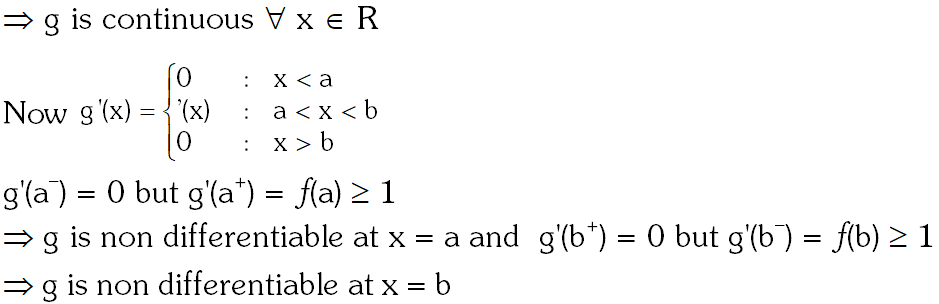
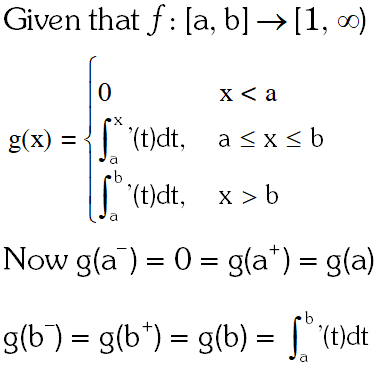
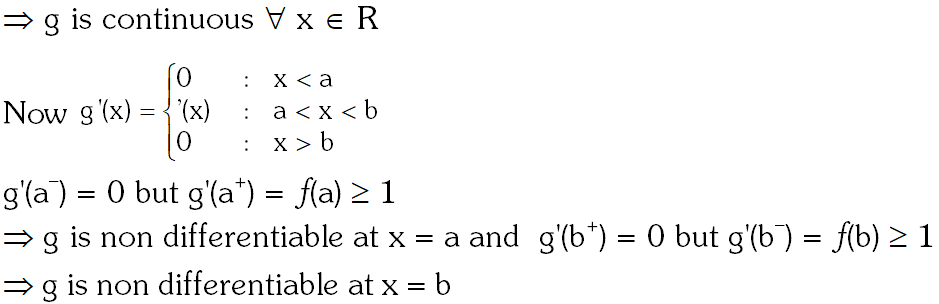
Q. The value of $\int_{0}^{1} 4 x^{3}\left\{\frac{d^{2}}{d x^{2}}\left(1-x^{2}\right)^{5}\right\} d x$ is
[JEE(Advanced)-2014, 3]
Ans. 2
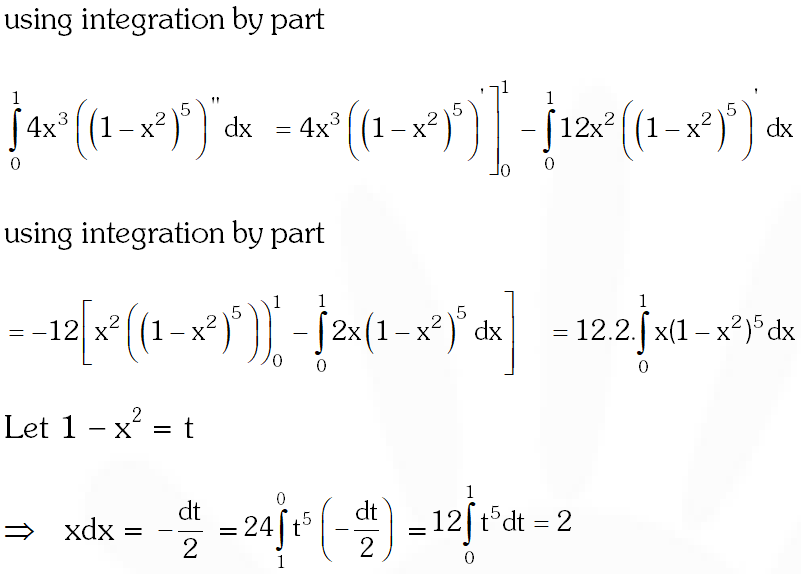
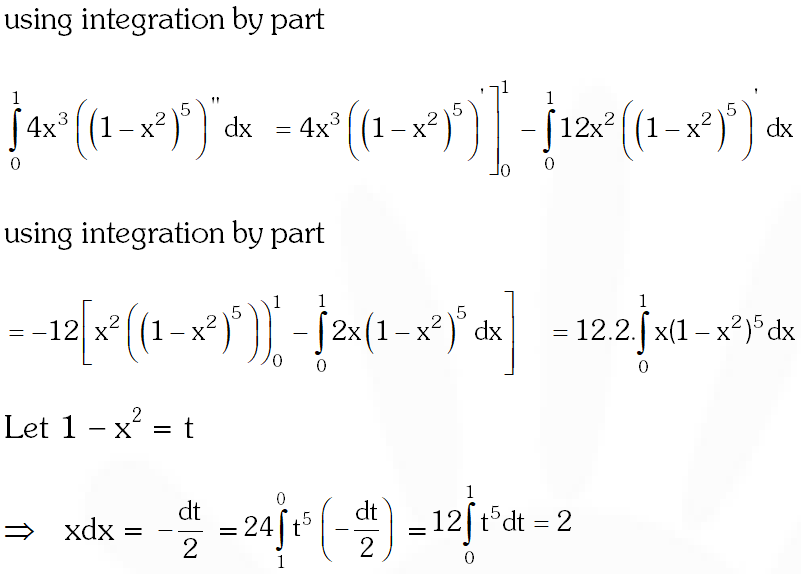
Q. The following integral $\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(2 \csc x)^{17} d x$ is equal to
(A) $\int_{0}^{\log (1+\sqrt{2})} 2\left(e^{\mathfrak{u}}+e^{-\mathfrak{u}}\right)^{16} \mathrm{d} \mathfrak{u}$
(B) $\int_{0}^{\log (1+\sqrt{2})}\left(\mathrm{e}^{\mathrm{u}}+\mathrm{e}^{-\mathrm{u}}\right)^{17} \mathrm{du}$
(C) $\int_{0}^{\log (1+\sqrt{2})}\left(e^{\mathfrak{u}}-e^{-\mathfrak{u}}\right)^{17} \mathrm{d} \mathfrak{u}$
(D) $\int_{0}^{\log (1+\sqrt{2})} 2\left(e^{\mathfrak{u}}-e^{-\mathfrak{u}}\right)^{16} d \mathfrak{u}$
[JEE(Advanced)-2014, 3(–1)]
Ans. (A)
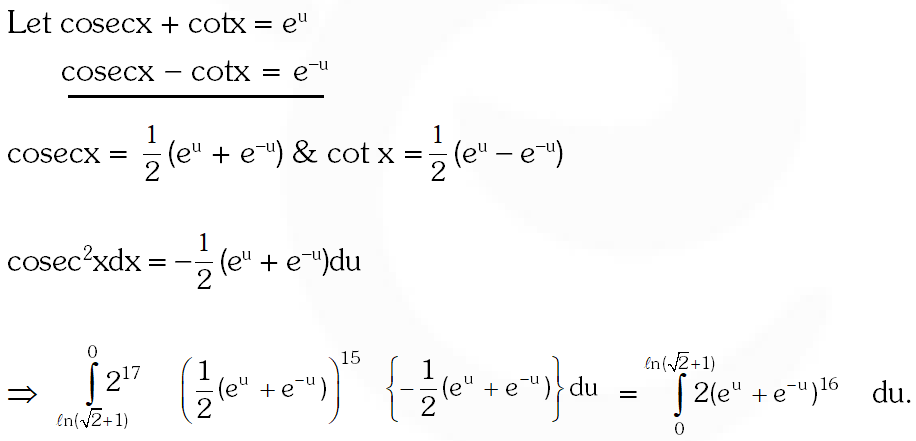
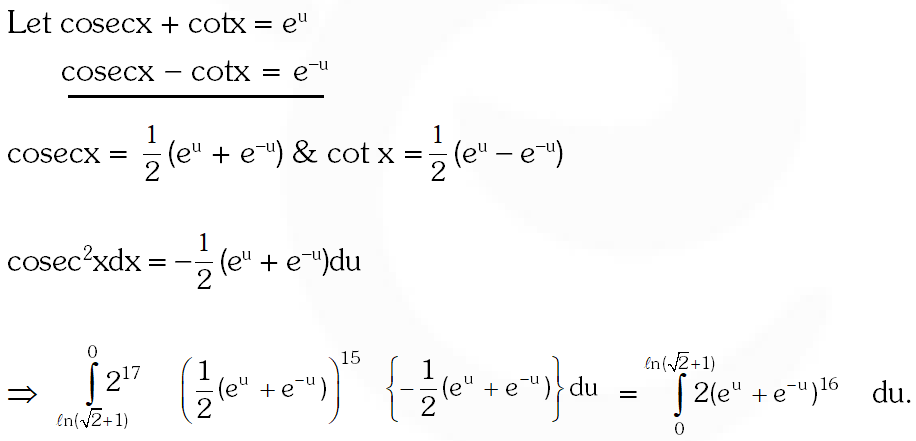
Q. Let $f:[0,2] \rightarrow \square$ be a function which is continuous on $[0,2]$ and is differentiable on $(0,2)$ with $f(0)=1 .$ Let $F(x)=\int_{0}^{x^{2}} f(\sqrt{t}) d t$ for $x \in[0,2] .$ If $F^{\prime}(x)=f^{\prime}(x)$ for all $x \in(0,2)$ then $F(2)$ equals $-$
(A) $\mathrm{e}^{2}-1$
(B) $\mathrm{e}^{4}-1$
(C) e – 1
(D) e $^{4}$
[JEE(Advanced)-2014, 3(–1)]
Ans. (B)
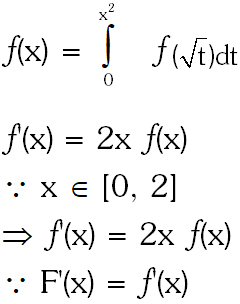
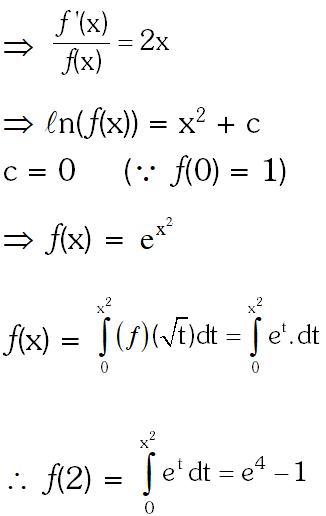
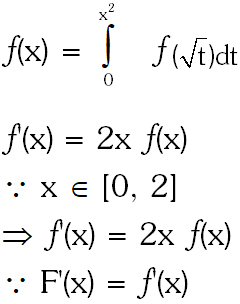
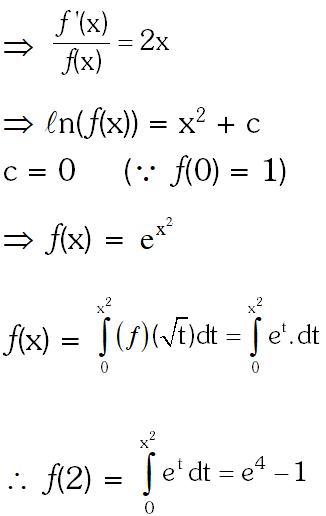
Q. The value of $\mathrm{g}\left(\frac{1}{2}\right)$ is –
(A) $\pi$
(B) $2 \pi$
(C) $\frac{\pi}{2}$
(D) $\frac{\pi}{4}$
[JEE(Advanced)-2014, 3(–1)]
Ans. (A)
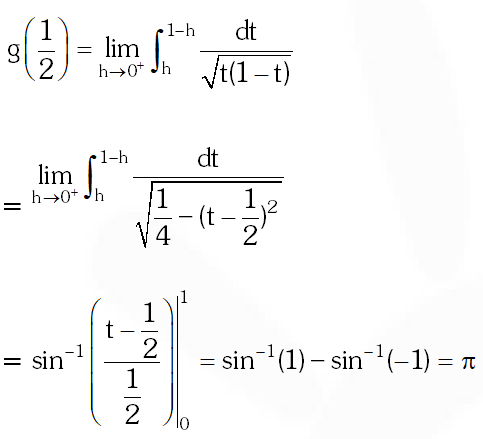
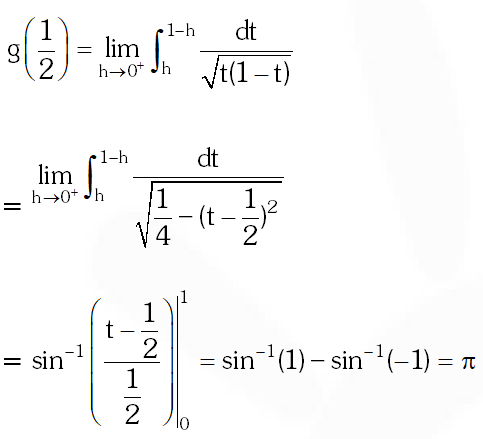
Q. The value of $\mathrm{g}^{\prime}\left(\frac{1}{2}\right)$ is-
(A) $\frac{\pi}{2}$
(B) $\pi$
(C) $-\frac{\pi}{2}$
(D) 0
[JEE(Advanced)-2014, 3(–1)]
Ans. (D)
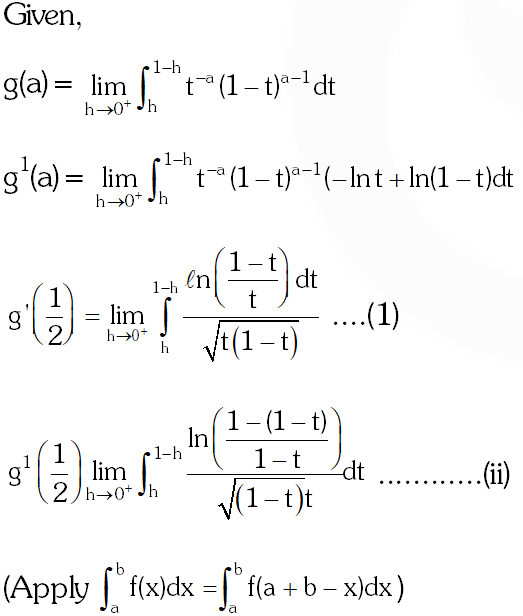
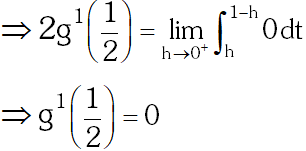
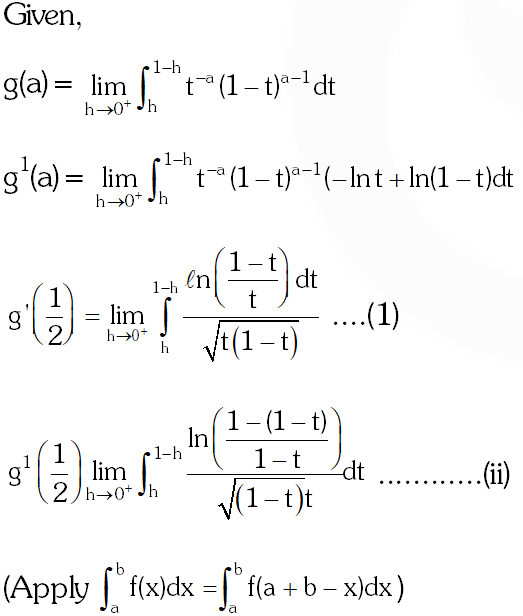
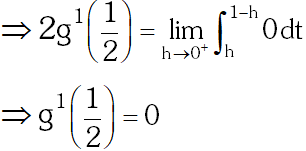
Q.
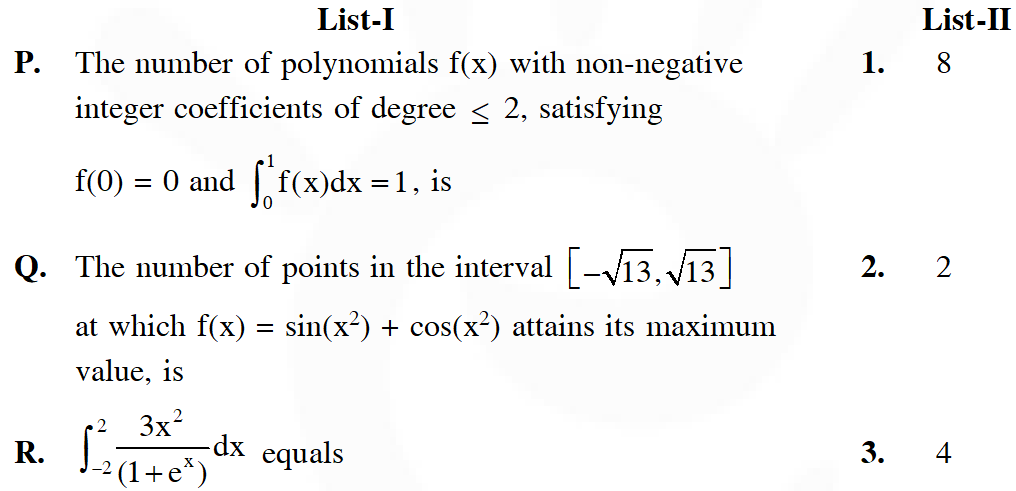
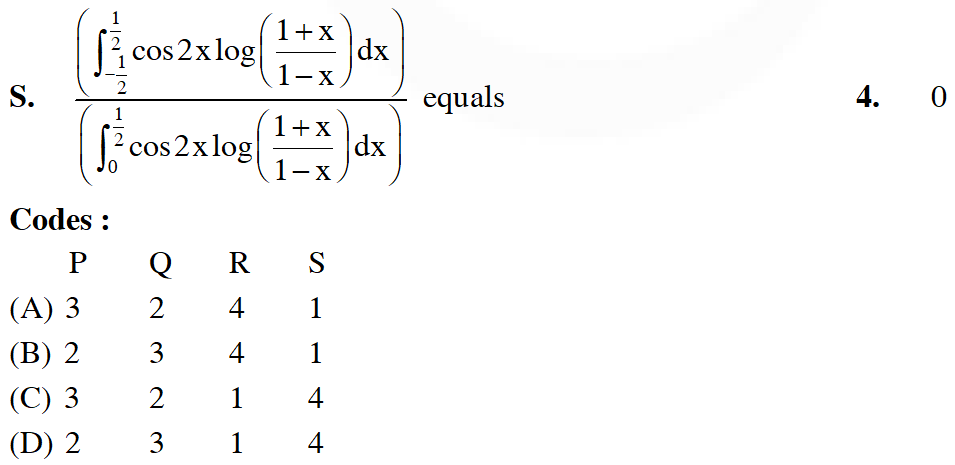 [JEE(Advanced)-2014, 3(–1)]
[JEE(Advanced)-2014, 3(–1)]
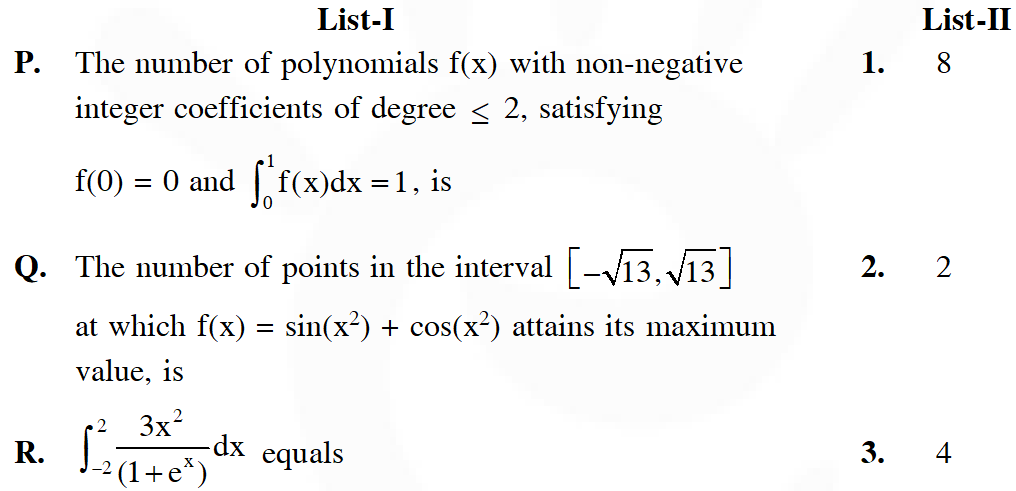
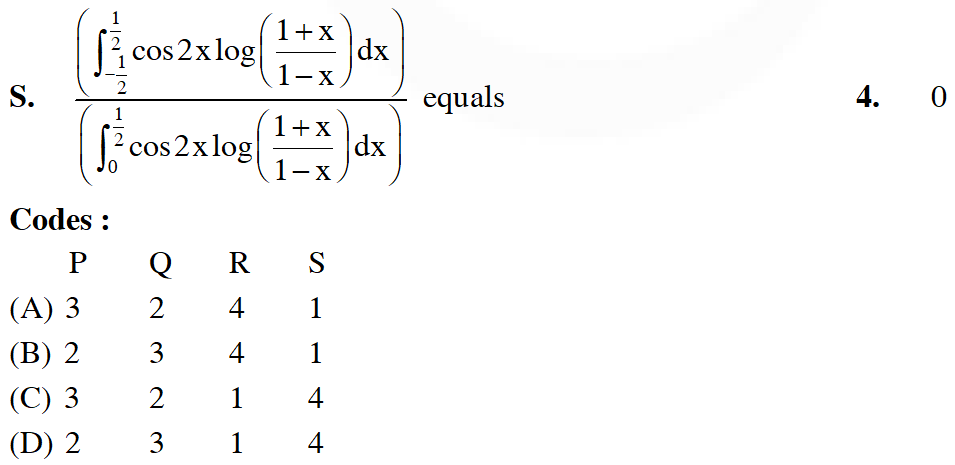 [JEE(Advanced)-2014, 3(–1)]
[JEE(Advanced)-2014, 3(–1)]
Ans. (C)
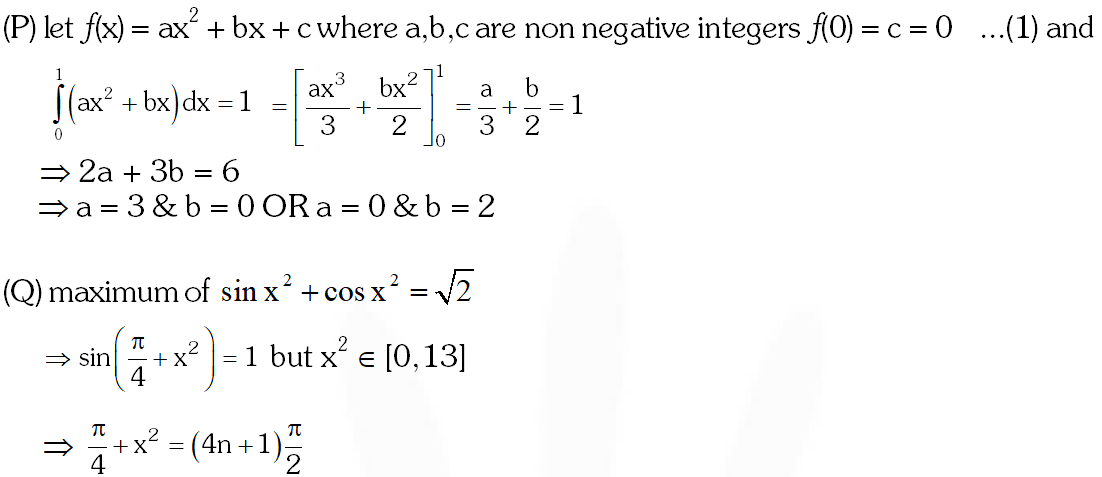
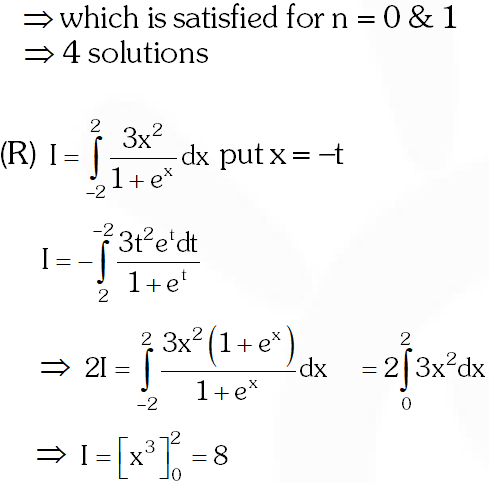
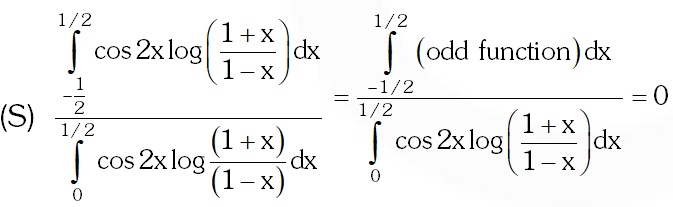
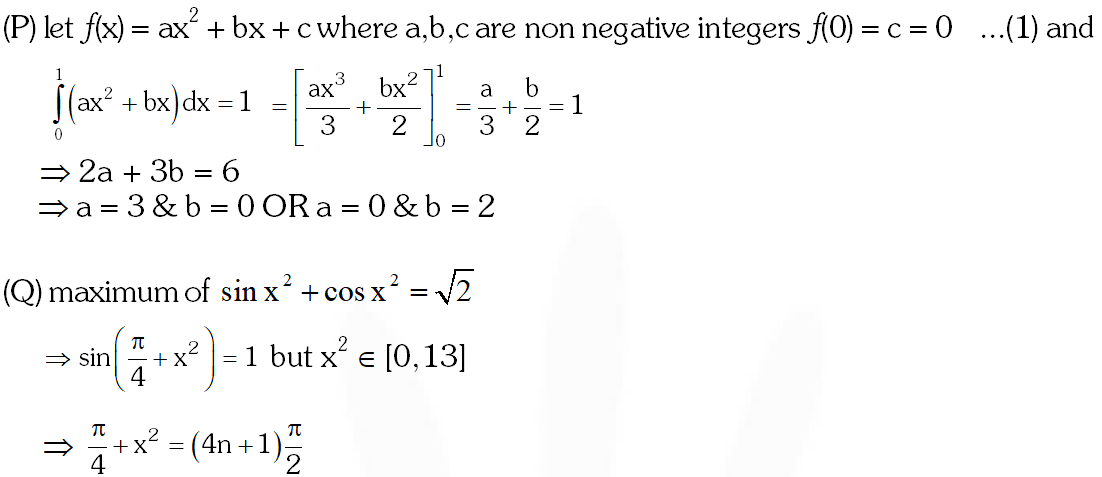
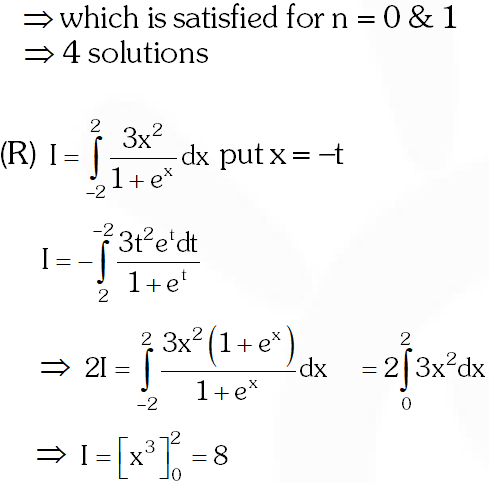
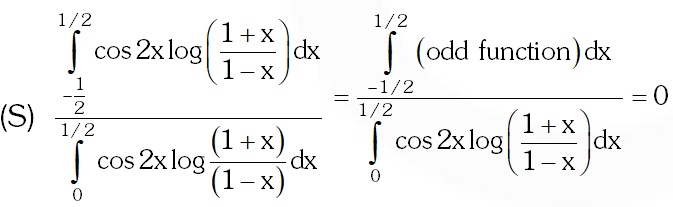
Q. Let $f: \square \rightarrow \square$ be a function defined by $f(x)$ $=\left\{\begin{array}{ccc}{[\mathrm{x}]} & {,} & {\mathrm{x} \leq 2} \\ {0} & {,} & {\mathrm{x}>2}\end{array}\right.$ where [x] is the greatest integer less than or equal to x. If $\mathrm{I}=\int_{-1}^{2} \frac{\mathrm{x} f\left(\mathrm{x}^{2}\right)}{2+f(\mathrm{x}+1)} \mathrm{dx}$ , then the value of (4I – 1) is
[JEE 2015, 4M, –0M]
Ans. (A)
Q. If $\alpha=\int_{0}^{1}\left(\mathrm{e}^{9 \mathrm{x}+3 \tan ^{-1} \mathrm{x}}\right)\left(\frac{12+9 \mathrm{x}^{2}}{1+\mathrm{x}^{2}}\right) \mathrm{d} \mathrm{x}$ where $\tan ^{-1} \mathrm{x}$ takes only principal values, then the value of $\left(\log _{\mathrm{e}}|1+\alpha|-\frac{3 \pi}{4}\right)$ is
[JEE 2015, 4M, –0M]
Ans. 0
Q. Let $f: \mathbb{U} \rightarrow \square$ be a continuous odd function, which vanishes exactly at one point and $f(1)=\frac{1}{2}$ Suppose that $\mathrm{F}(\mathrm{x})=\int_{-1}^{\mathrm{x}} f(\mathrm{t}) \mathrm{dt}$ for all $\mathrm{x} \in[-1,2]$ and $\mathrm{G}(\mathrm{x})$ $=\int_{-1}^{x} \mathfrak{t}|f(f(\mathfrak{t}))| d \mathfrak{t}$ for all $x \in[-1,2]$. If $\lim _{x \rightarrow 1} \frac{F(x)}{G(x)}=\frac{1}{14},$ then the value of $f\left(\frac{1}{2}\right)$ is
[JEE 2015, 4M, –0M]
Ans. 9
Q. The option(s) with the values of a and L that satisfy the following equation is(are)
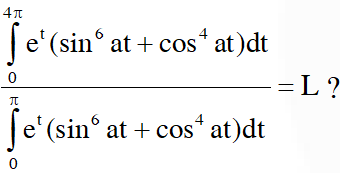 (A) $a=2, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(B) $a=2, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$c
(C) $a=4, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(D) $a=4, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$
[JEE 2015, 4M, –0M]
(A) $a=2, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(B) $a=2, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$c
(C) $a=4, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(D) $a=4, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$
[JEE 2015, 4M, –0M]
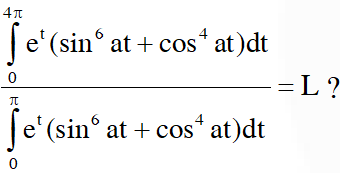 (A) $a=2, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(B) $a=2, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$c
(C) $a=4, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(D) $a=4, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$
[JEE 2015, 4M, –0M]
(A) $a=2, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(B) $a=2, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$c
(C) $a=4, L=\frac{e^{4 \pi}-1}{e^{\pi}-1}$
(D) $a=4, L=\frac{e^{4 \pi}+1}{e^{\pi}+1}$
[JEE 2015, 4M, –0M]
Ans. 7
Q. Let $f(\mathrm{x})=7 \tan ^{8} \mathrm{x}+7 \tan ^{6} \mathrm{x}-3 \tan ^{4} \mathrm{x}-3 \tan ^{2} \mathrm{x}$ for all $\mathrm{x} \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) .$ Then the correct expression(s)is(are)
(A) $\int_{0}^{\pi / 4} \mathrm{x} f(\mathrm{x}) \mathrm{d} \mathrm{x}=\frac{1}{12}$
(B) $\int_{0}^{\pi / 4} f(\mathrm{x}) \mathrm{d} \mathrm{x}=0$
(C) $\int_{0}^{\pi / 4} \mathrm{x} f(\mathrm{x}) \mathrm{d} \mathrm{x}=\frac{1}{6}$
(D) $\int_{0}^{\pi / 4} f(\mathrm{x}) \mathrm{d} \mathrm{x}=1$
[JEE 2015, 4M, –0M]
Ans. (A,C)
Q. Let $f^{\prime}(x)=\frac{192 x^{3}}{2+\sin ^{4} \pi x}$ for all $\mathrm{x} \in \square$ with $f$ $\left(\frac{1}{2}\right)$ $=0 .$ If $\mathrm{m} \leq \int_{1 / 2}^{1} f(\mathrm{x}) \mathrm{d} \mathrm{x} \leq \mathrm{M}$ then the possible values of m and M are
(A) m = 13, M = 24
(B) $\quad \mathrm{m}=\frac{1}{4}, \mathrm{M}=\frac{1}{2}$
(C) m = –11, M = 0
(D) m = 1, M = 12
[JEE 2015, 4M, –0M]
Ans. (A,B)
Q. The correct statement(s) is(are)
(A) $f^{\prime}(1)<0$
(B) $f(2)<0$
(C) $f^{\prime}(\mathrm{x}) \neq 0$ for any $\mathrm{x} \in(1,3)$
(D) $f^{\prime}(x)=0$ for some $x \in(1,3)$
[JEE 2015, 4M, –0M]
Ans. (D)
Q. If $\int_{1}^{3} \mathrm{x}^{2} \mathrm{F}^{\prime}(\mathrm{x}) \mathrm{d} \mathrm{x}=-12$ and $\int_{1}^{3} \mathrm{x}^{3} \mathrm{F}^{\prime \prime}(\mathrm{x}) \mathrm{d} \mathrm{x}=40,$ then the correct expression(s) is (are)
(A) 9ƒ'(3) + ƒ'(1) – 32 = 0
(B) $\int_{1}^{3} f(\mathrm{x}) \mathrm{d} \mathrm{x}=12$
(C) 9ƒ'(3) – ƒ'(1) + 32 = 0
(D) $\left.\int_{1}^{3} f(x) d x=-12\right]$
[JEE 2015, 4M, –0M]
Ans. (A,B,C)
Q. The value of $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{x^{2} \cos x}{1+e^{x}} d x$ is equal to
(A) $\frac{\pi^{2}}{4}-2$
(B) $\frac{\pi^{2}}{4}+2$
(C) $\pi^{2}-\mathrm{e}^{\frac{\pi}{2}}$
(D) $\pi^{2}+\mathrm{e}^{\frac{\pi}{2}}$
[JEE(Advanced)2016]
Ans. (C,D)
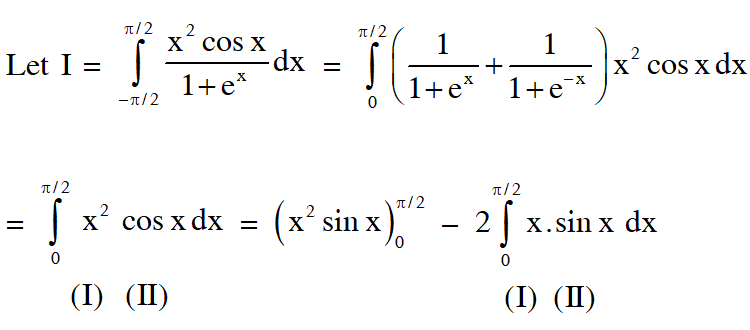
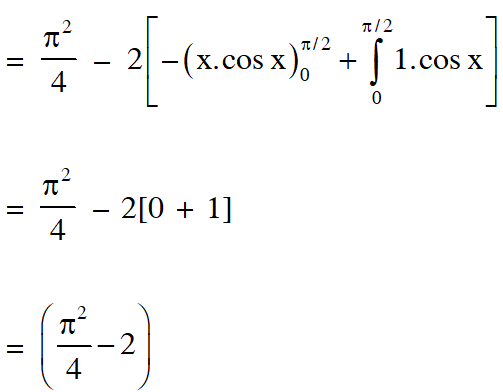
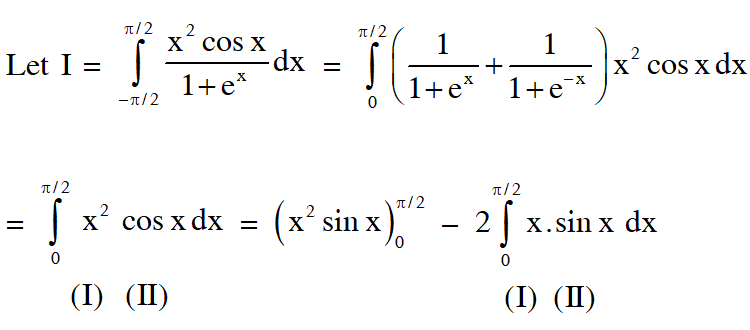
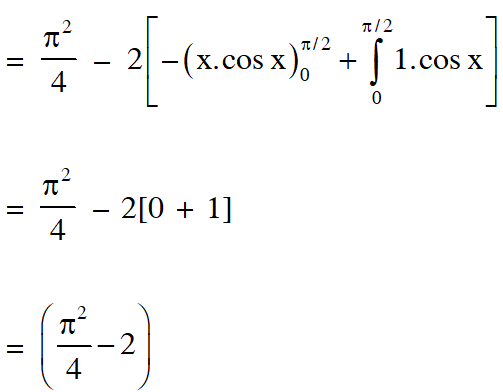
Q. Let $\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}$ be a differentiable function such that $\mathrm{f}(0)=0, \mathrm{f}\left(\frac{\pi}{2}\right)=3$ and $\mathrm{f}^{\prime}(0)=1$ If $\mathrm{g}(\mathrm{x})=\int_{\mathrm{x}}^{\frac{\pi}{2}}\left[\mathrm{f}^{\prime}(\mathrm{t}) \csc \mathrm{t}-\cot t \csc \mathrm{t} \mathrm{f}(\mathrm{t})\right] \mathrm{d} \mathrm{t}$ for $\mathrm{x} \in\left(0, \frac{\pi}{2}\right],$ then $\lim _{\mathrm{x} \rightarrow 0} \mathrm{g}(\mathrm{x})=$
[JEE(Advanced)-2017]
Ans. 2
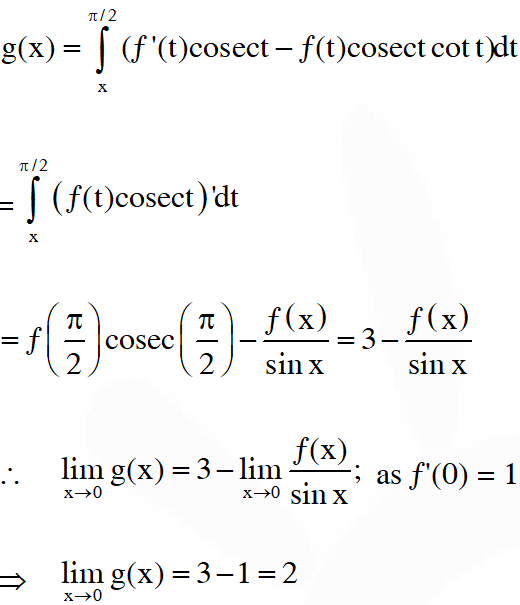
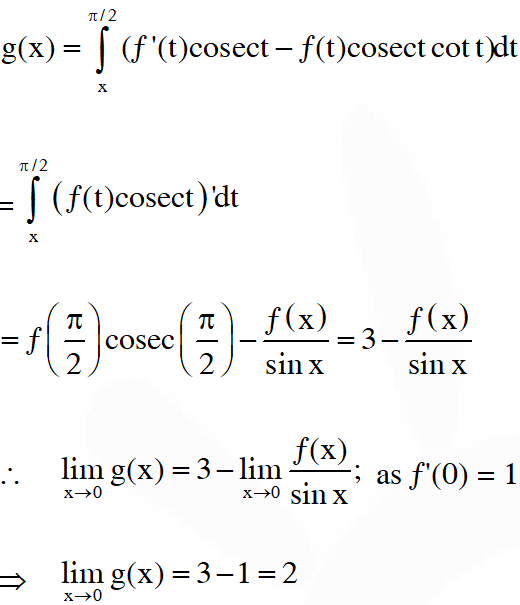
Q. If $\mathrm{I}=\sum_{\mathrm{k}=1}^{98} \int_{\mathrm{k}}^{\mathrm{k}+1} \frac{\mathrm{k}+1}{\mathrm{x}(\mathrm{x}+1)} \mathrm{d} \mathrm{x},$ then
(A) $\mathrm{I}<\frac{49}{50}$
(B) $\mathrm{I}<\log _{\mathrm{e}} 99$
(C) $\mathrm{I}>\frac{49}{50}$
(D) $\mathrm{I}>\log _{\mathrm{e}} 99$
[JEE(Advanced)-2017]
Ans. (B,C)
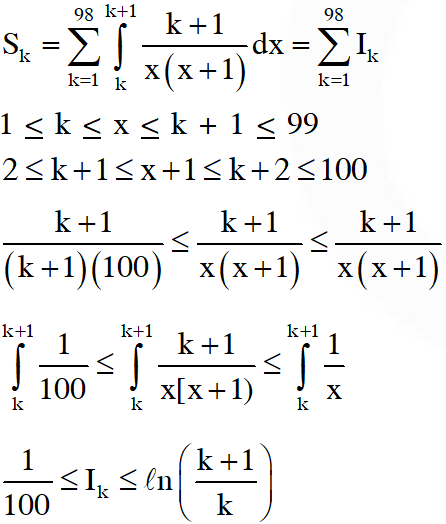
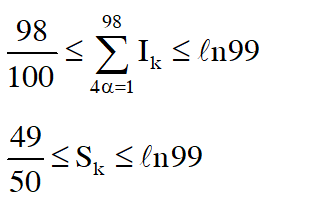
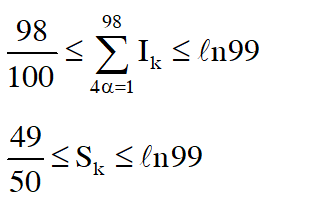
Q. If $\mathrm{g}(\mathrm{x})=\int_{\sin \mathrm{x}}^{\sin (2 \mathrm{x})} \sin ^{-1}(\mathrm{t}) \mathrm{dt},$ then
(A) $\mathrm{g}^{\prime}\left(\frac{\pi}{2}\right)=-2 \pi$
(B) $\mathrm{g}^{\prime}\left(-\frac{\pi}{2}\right)=2 \pi$
(C) $\mathrm{g}^{\prime}\left(\frac{\pi}{2}\right)=2 \pi$
(D) $\mathrm{g}^{\prime}\left(-\frac{\pi}{2}\right)=-2 \pi$
[JEE(Advanced)-2017]
Ans. (Bonus)
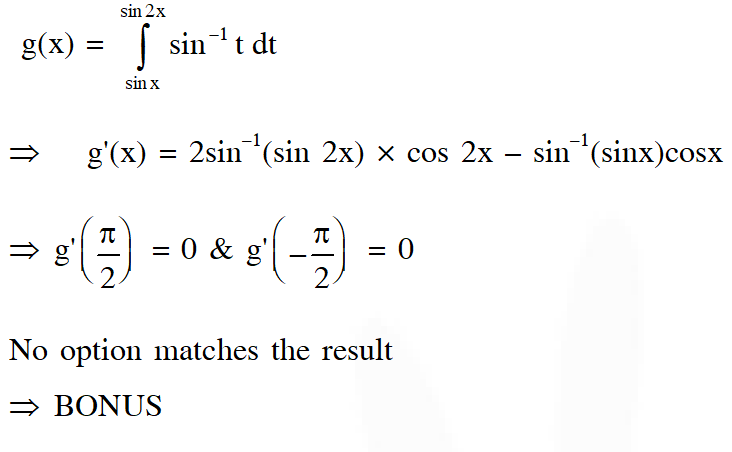
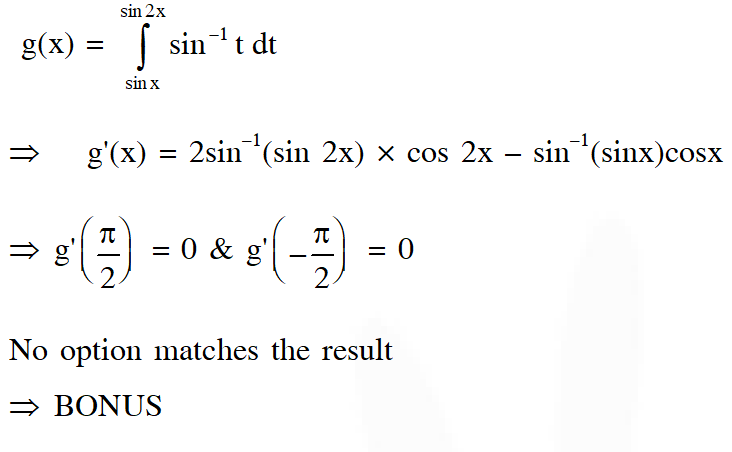
Q. The value of the integral $\int_{0}^{\frac{1}{2}} \frac{1+\sqrt{3}}{\left((x+1)^{2}(1-x)^{6}\right)^{\frac{1}{4}}} d x$ is
[JEE(Advanced)-2018]
Ans. 2
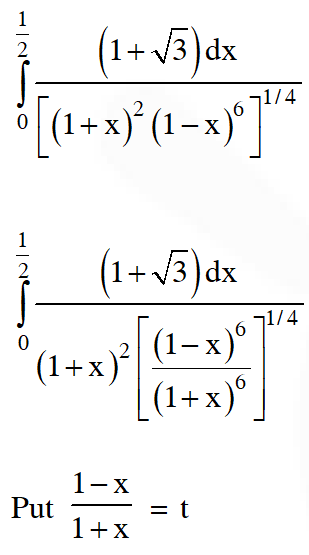
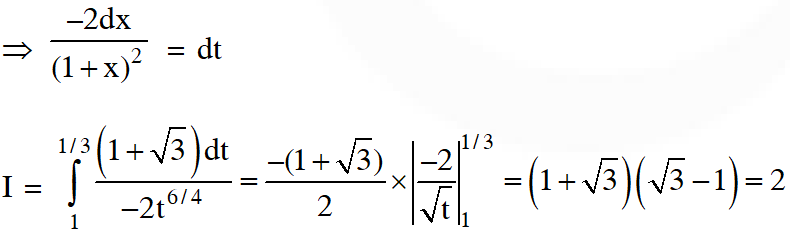
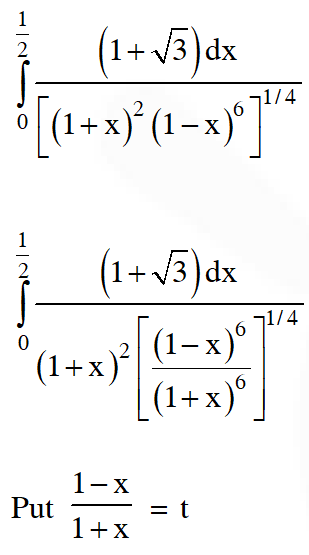
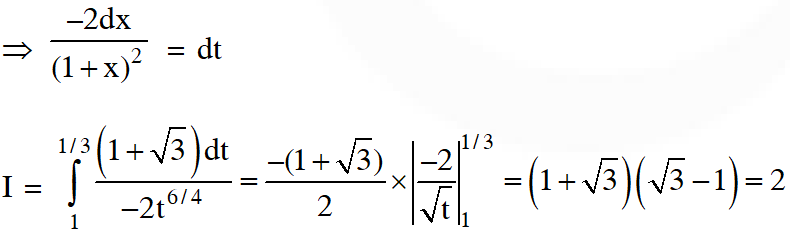
Comments
Shaurya
Sept. 20, 2021, 8:15 p.m.
Jee advance 2014 Matching wale ques mein Pth me 2 functions hi possible honge.
How u have found 4?
Lavanya
June 11, 2021, 10:33 p.m.
Key to question numbers 18,19,20,21 is messed up!please correct it🙃
