A toroid works as an inductor, which boosts the frequency to appropriate levels. Inductors are electronic components that are passive so that they can store energy in the form of magnetic fields. A toroid turns, and with those turns induces a higher frequency. Toroids are more economical and efficient than solenoids. So here we will study in detail about solenoids and Toroids and the differences between both.
A toroid is often used to create an almost uniform magnetic field in some enclosed area.
The device consists of a conducting wire wrapped around a ring (a torus) made of a non-conducting material.
Let a toroid having N closely spaced turns of wire,
the magnetic field in the region occupied by the torus = B
Radius of the Toroid ring = R
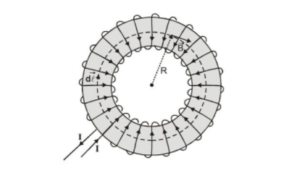To calculate the field, we must evaluate $\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}$ over the circle of radius $\mathrm{R} .$ By symmetry magnitude of the field is constant at the circumference of the circle and tangent to it.
So, $\quad \quad \oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \vec{\ell}=\mathrm{B} \ell=\mathrm{B}(2 \pi \mathrm{R})$
This result shows that $\mathrm{B} \propto \frac{1}{\mathrm{R}}$ and hence is nonuniform in the region occupied by torus. However,
if R is very large compared with the cross-sectional radius of the torus, then the field is approximately uniform inside the torus.
Number of turns per unit length of torus $n=\frac{N}{2 \pi R}$
$\therefore \quad B=\mu_{0} n I$
For an ideal toroid, in which turns are closely spaced, the external magnetic field is zero. This is because the net current passing through any circular path laying outside the toroid is zero. Therefore, from Ampere's law, we find that $B=0,$ in the regions exterior to the torus.
Toroid
A toroid is an endless solenoid in the form of a ring, as shown in fig.A toroid is often used to create an almost uniform magnetic field in some enclosed area.
The device consists of a conducting wire wrapped around a ring (a torus) made of a non-conducting material.
Let a toroid having N closely spaced turns of wire,
the magnetic field in the region occupied by the torus = B
Radius of the Toroid ring = R
To calculate the field, we must evaluate $\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}$ over the circle of radius $\mathrm{R} .$ By symmetry magnitude of the field is constant at the circumference of the circle and tangent to it.
So, $\quad \quad \oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \vec{\ell}=\mathrm{B} \ell=\mathrm{B}(2 \pi \mathrm{R})$
This result shows that $\mathrm{B} \propto \frac{1}{\mathrm{R}}$ and hence is nonuniform in the region occupied by torus. However,
if R is very large compared with the cross-sectional radius of the torus, then the field is approximately uniform inside the torus.
Number of turns per unit length of torus $n=\frac{N}{2 \pi R}$
$\therefore \quad B=\mu_{0} n I$
For an ideal toroid, in which turns are closely spaced, the external magnetic field is zero. This is because the net current passing through any circular path laying outside the toroid is zero. Therefore, from Ampere's law, we find that $B=0,$ in the regions exterior to the torus.
Solenoid:
A long wire wrapped around in a helical shape is known as Solenoid. They are cylindrical in shape as you can see in the image above. A solenoid is used in experiments and research field regarding the magnetic field. The magnetic field inside the solenoid is uniform.Difference between Solenoid and Toroid
Solenoid and toroid both work on the principle of electromagnetism and both behave like an electromagnet when the current is passed. The magnetic field produces by them is $\mathrm{B}=$ Uo.ni. Even after having so many similarities solenoid and toroid differs in property such as shape:
Solenoid |
Toroid |
| Cylindrical in shape | Circular in shape |
| Magnetic field is created outside | Magnetic field is created within |
| Magnetic field is created outside | It does not have a uniform magnetic field inside it. |
| Has uniform magnetic field inside it. | Magnetic feild Outside :- magnetic field (B) $=0$ |
| Magnetic feild due to solenoid is $(B)=$ Uo.nì | Magnetic feild Inside:-Magnetic field $(B)=0$ |
| Magnetic feild Within the toroid:- Magnetic field (B) = Uo.ni |
Similarities between Solenoid and Toroid
- Both works on the principle of Electromagnetism.
- When the current is passed through them, they both act as an electromagnet.
- Magnetic field due to the solenoid and within the toroid is the same. B = Uo.ni