The Solenoid is a coil of wire that acts like an electromagnet when a flow of electricity passes through it. Electromagnetic solenoids find use all over the world. You can hardly swing a bat without hitting a solenoid. Speakers and microphones both contain solenoids. In fact, a speaker and microphone are pretty much exactly the same things in reverse of each other. So here we will study in detail about Magnetic Field of a Solenoid Derivation in this article:
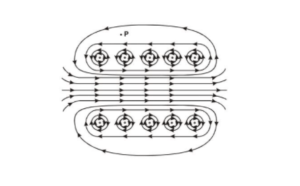
The figure shows the lines of force of the magnetic field due to a solenoid. The lines of force inside the solenoid are nearly parallel which indicates that the magnetic field 'within' the solenoid is uniform and parallel to the axis of the solenoid.
Let there be a long solenoid of radius 'a' and carrying a current I. Let n be the number of turns per unit length of the solenoid. Let $P$ be a point on the axis of the solenoid.
Let us imagine the solenoid to be divided up into a number of narrow coils and consider one such coil AB of width $\delta x$. The number of turns in this coil is n\deltax. Let $x$ be the distance of the point $P$ from the centre $\mathrm{C}$ of this coil. The magnetic field at $\mathrm{P}$ due to this elementary coil is given by
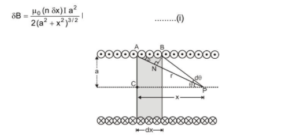Let average distance of circumference is r and $\delta \theta$ the angle subtended by the coil at P.
$$ \sin \theta=\frac{\mathrm{BN}}{\mathrm{AB}}=\frac{\mathrm{r} \delta \theta}{\delta \mathrm{x}} \quad \text { or } \quad \delta \mathrm{x}=\frac{\mathrm{r} \delta \theta}{\sin \theta} $$
In $\Delta \mathrm{ACP},$ we have $\quad \mathrm{a}^{2}+\mathrm{x}^{2}=\mathrm{r}^{2}$
$$ r^{3}=\left(a^{2}+x^{2}\right)^{3 / 2} $$
Substiuting these values of $\delta x$ and $\left(a^{2}+x^{2}\right)^{3 / 2}$ in eq. (i), we get
$$ \delta \mathrm{B}=\frac{\mu_{0}(\mathrm{nr} \delta \theta) \mathrm{I} \mathrm{a}^{2}}{2 \mathrm{r}^{3} \sin \theta}=\frac{\mu_{0} \mathrm{nI} \mathrm{a}^{2}}{2 \mathrm{r}^{2}} \frac{\delta \theta}{\sin \theta} $$
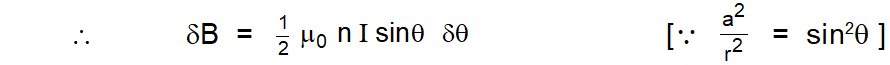
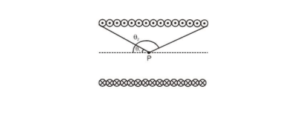
The magnetic field $\mathrm{B}$ at $\mathrm{P}$ due to the whole solenoid can be obtained by integrating the above expression between the limits $\theta_{1}$ and $\theta_{2},$ where $\theta_{1}$ and $\theta_{2}$ are the semi-vertical angles subtended at $P$ by the first and the last turn of the solenoid respectively. Thus
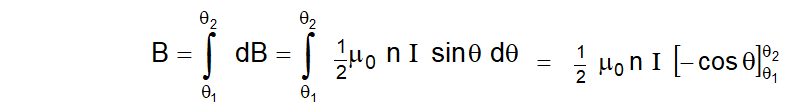
or $\quad \mathrm{B}=\frac{1}{2} \mu_{0} \mathrm{n} \mathrm{I}\left(\cos \theta_{1}-\cos \theta_{2}\right)$ ..........(ii)
If the observation point P is well inside a very long solenoid
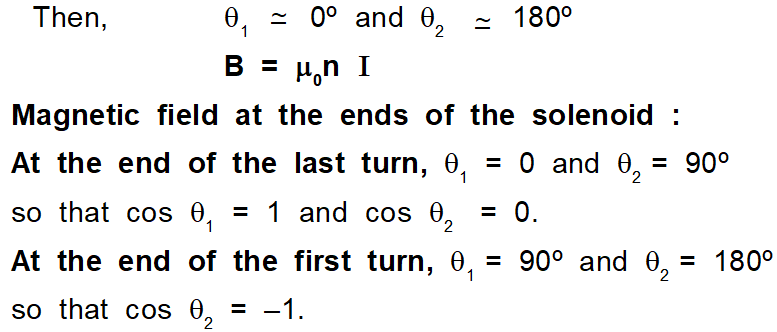
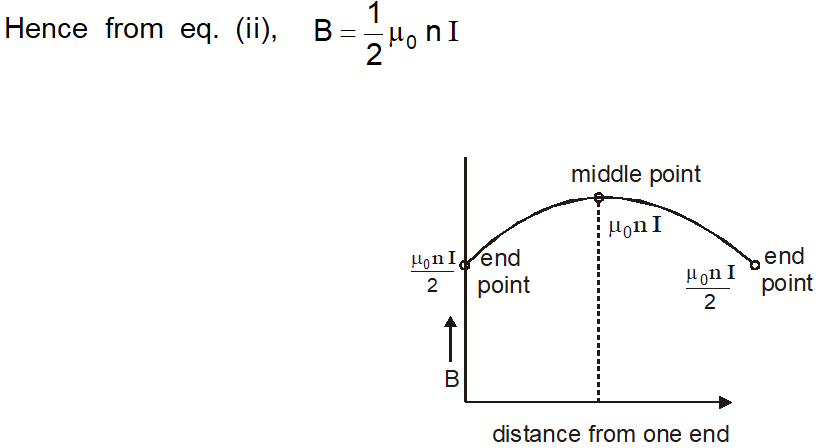
Thus, the magnetic field at the ends of a 'long' solenoid is half of that at the center. If the solenoid is sufficiently long, the field within it (except near the ends) in uniform. It does not depend upon the length and area of the cross-section of the solenoid. Just as a parallel-plate capacitor produces a uniform and known electric field, a solenoid produces a uniform and known magnetic field.
The 'uniform' magnetic field within a long solenoid is parallel to the solenoid axis.
Its direction along the axis is given by a curled-straight right-hand rule. "If we grasp the solenoid with our right hand so that our fingers follow the direction of the current in the winding's, then out extended right thumb will point in the direction of the axial magnetic field".
Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.
Magnetic Field of a Solenoid
A solenoid is a long cylindrical helix. It is made by winding closely a large number of turns of insulated copper wire over a tube of cardboard or china-clay. When an electric current is passed through the solenoid, a magnetic field is produced around and within the solenoid.The figure shows the lines of force of the magnetic field due to a solenoid. The lines of force inside the solenoid are nearly parallel which indicates that the magnetic field 'within' the solenoid is uniform and parallel to the axis of the solenoid.
Magnetic Field of a Solenoid Derivation
Let there be a long solenoid of radius 'a' and carrying a current I. Let n be the number of turns per unit length of the solenoid. Let $P$ be a point on the axis of the solenoid.
Let us imagine the solenoid to be divided up into a number of narrow coils and consider one such coil AB of width $\delta x$. The number of turns in this coil is n\deltax. Let $x$ be the distance of the point $P$ from the centre $\mathrm{C}$ of this coil. The magnetic field at $\mathrm{P}$ due to this elementary coil is given by
Let average distance of circumference is r and $\delta \theta$ the angle subtended by the coil at P.
$$ \sin \theta=\frac{\mathrm{BN}}{\mathrm{AB}}=\frac{\mathrm{r} \delta \theta}{\delta \mathrm{x}} \quad \text { or } \quad \delta \mathrm{x}=\frac{\mathrm{r} \delta \theta}{\sin \theta} $$
In $\Delta \mathrm{ACP},$ we have $\quad \mathrm{a}^{2}+\mathrm{x}^{2}=\mathrm{r}^{2}$
$$ r^{3}=\left(a^{2}+x^{2}\right)^{3 / 2} $$
Substiuting these values of $\delta x$ and $\left(a^{2}+x^{2}\right)^{3 / 2}$ in eq. (i), we get
$$ \delta \mathrm{B}=\frac{\mu_{0}(\mathrm{nr} \delta \theta) \mathrm{I} \mathrm{a}^{2}}{2 \mathrm{r}^{3} \sin \theta}=\frac{\mu_{0} \mathrm{nI} \mathrm{a}^{2}}{2 \mathrm{r}^{2}} \frac{\delta \theta}{\sin \theta} $$
The magnetic field $\mathrm{B}$ at $\mathrm{P}$ due to the whole solenoid can be obtained by integrating the above expression between the limits $\theta_{1}$ and $\theta_{2},$ where $\theta_{1}$ and $\theta_{2}$ are the semi-vertical angles subtended at $P$ by the first and the last turn of the solenoid respectively. Thus
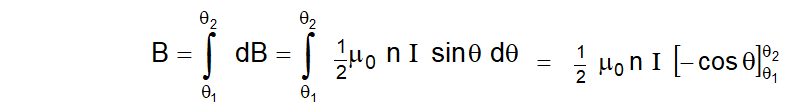
or $\quad \mathrm{B}=\frac{1}{2} \mu_{0} \mathrm{n} \mathrm{I}\left(\cos \theta_{1}-\cos \theta_{2}\right)$ ..........(ii)
If the observation point P is well inside a very long solenoid
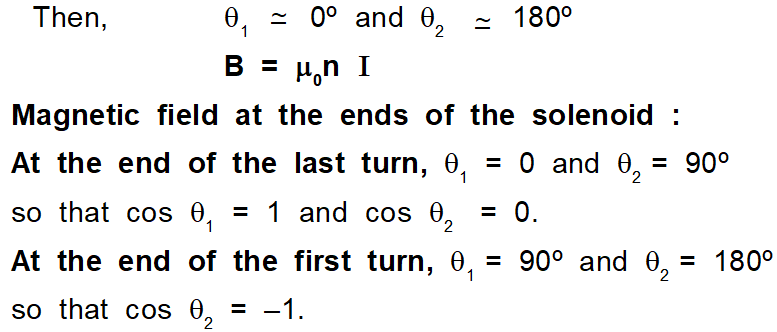
Thus, the magnetic field at the ends of a 'long' solenoid is half of that at the center. If the solenoid is sufficiently long, the field within it (except near the ends) in uniform. It does not depend upon the length and area of the cross-section of the solenoid. Just as a parallel-plate capacitor produces a uniform and known electric field, a solenoid produces a uniform and known magnetic field.
The 'uniform' magnetic field within a long solenoid is parallel to the solenoid axis.
Its direction along the axis is given by a curled-straight right-hand rule. "If we grasp the solenoid with our right hand so that our fingers follow the direction of the current in the winding's, then out extended right thumb will point in the direction of the axial magnetic field".
Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.