Hey, do you want to learn about the Efficiency of Carnot engine? If so. Then keep reading
There are four thermodynamical processes isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression.
Mechanical Arrangements and working substance: A cylinder whose walls are perfectly non-conducting but base perfectly conducting fitted with non-conducting piston which can move without any frictional losses. Ideal gas enclosed in these systems as a working substance.
Heat sink: A cold body at low temperature $\mathrm{T}_{2} \mathrm{~K}$ to which the heat can be rejected. It is a body of large heat capacity. Its upper surface is highly conducting so that the working substance can reject heat to it.
Stand: It is made by perfectly insulating material so that when cylinder placed on it working substance can expended or compressed adiabaticly.
Working: To get maximum work from this type of ideal engine there is a set of reversible processes through then working substance is taken back to the Initial condition. The complete Carnot cycle is divided in four steps.
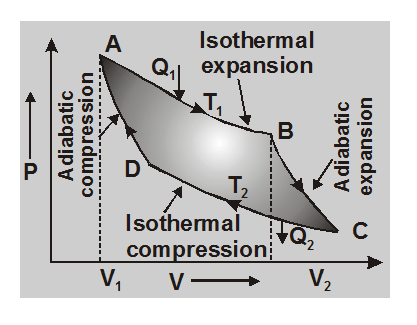
Processes of Carnot's cycle can be denoted by an indicator diagram a shown here in these diagram variation of pressure (P) and volume (V) of working substance (ideal gas), are plotted.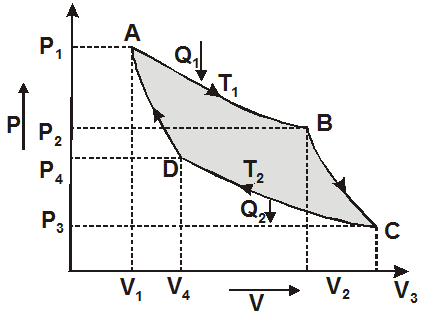
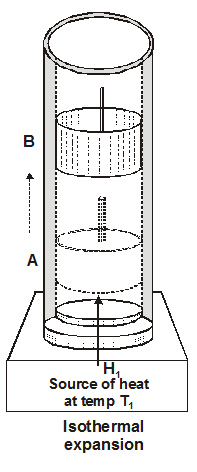
Initially the cyclinder is taken to be in thermal equilbrium with the high temperature $T_{1}$ represented by point $A$
$\left(P_{1}, \quad V_{1}, T_{1}\right)$
This is initial state of working substance (ideal gas)
Then the piston is allowed to move outward s owly. With the
movement of the piston, the temperature of the gas tends to fall. The process is very slow so that it is isothermal. Heat fom reservoir flows into the gas and temperature of the gas remains $\mathrm{T}_{1}$. In this expasion gas receive heat $\mathrm{Q}_{1}$ from source and gets state $\mathrm{B}\left(\mathrm{P}_{2}, \mathrm{~V}_{2}, \mathrm{~T}_{1}\right)$
The total heat input $Q_{1}$ to the gas occurs over the path from $A$ to $B$ and comes from a large reservoir of heat (source) at temperature $\mathrm{T}_{1}$ and utilized for doing work $W_{1}$.
Over the path from A to B the heat input to the gas equals the work done against the external pressure.
$\mathrm{G}_{1}=\int_{\mathrm{V}_{1}}^{\mathrm{V}_{2}} \mathrm{P} \mathrm{d} \mathrm{V}=\int_{\mathrm{V}_{1}}^{\mathrm{V}_{2}} \frac{\mu \mathrm{R} \mathrm{T}_{1}}{\mathrm{~V}}$
$\mathrm{d} \mathrm{V}=\mu \mathrm{R} \mathrm{T}_{1} \ln \left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)$
$W_{1}=\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)$
$\left(W_{1}=Q_{1}\right)$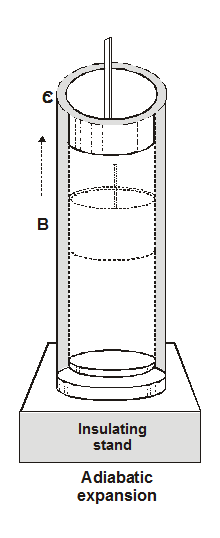
Now the contact of cylinder with source is removed and cylinder is put in contact with a non-conducting stand. The piston is allowed to move outward the gas now expands adiabatically because no heat can enter in or leave out. The tempeature falls to $\mathrm{T}_{2}$ and gas describes the adiabatic $\mathrm{BC}$ to point $\mathrm{C}\left(\mathrm{P}_{3}, \mathrm{~V}_{3}, \mathrm{~T}_{2}\right)$ during which more work is done $\left(\mathrm{W}_{2}\right)$ at the expense of the internal energy.
Work done over this adiabatic path BC is
$\mathrm{W}_{2}=\frac{\mu \mathrm{R}}{\gamma-1}\left(\mathrm{~T}_{1}-\mathrm{T}_{2}\right)$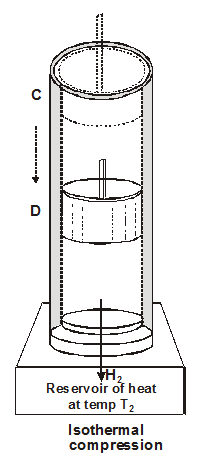
The gas cylinder is placed in contact with sink at temperature $\mathrm{T}_{2} .$ The piston is moved slowly inward so that heat produced during compression passes to the sink. The gas is isothermally compressed to point D. $\left(P_{4}, V_{4}, T_{2}\right)$
The heat rejected $\mathrm{Q}_{2}$ to the cold reservoir (sink) at $\mathrm{T}_{2}$ occurs over the path from $C$ to $D .$
The amount of work done on the gas $\mathrm{W}_{3}$ is equal to the amount of heat rejected to the sink
$\mathrm{W}_{3}=\mathrm{Q}_{2}$
So that
$\mathrm{W}_{3}=\mu \mathrm{RT}_{2} \ln \left(\frac{\mathrm{V}_{4}}{\mathrm{~V}_{3}}\right)$
or $\mathrm{Q}_{2}=\mu \mathrm{RT}_{2} \ln \left(\frac{\mathrm{V}_{4}}{\mathrm{~V}_{3}}\right)$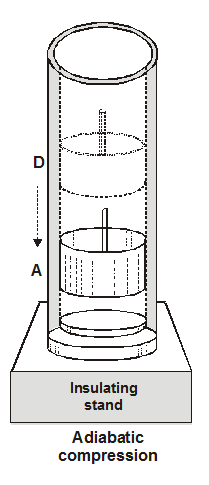
The cylinder is removed from the sink and is put in contact with insulating stand and piston moves inward. Heat is not allowed to go out and it increases the internal energy of the system. Then work done on the gas during adiabatic compression from state $D$ to initial point $A\left(P_{1}, V_{1}, T_{1}\right)$
No heat exchanges occur over the adiabatic path.
Work done on the system is
$W_{4}=\frac{\mu R}{\gamma-1}\left(T_{2}-T_{1}\right)$
This cycle of operations is called a Carnot cycle. In first two steps work is done by engine $\left(\mathrm{W}_{1}\right.$ and $\mathrm{W}_{2}$ are positive) and in last two steps work is done on gas $\left(\mathrm{W}_{3}\right.$ and $\mathrm{W}_{4}$ are negative)
The work done in complete cylce W is equal to the area of the closed part of the P–V cycle.
$W=W_{1}+W_{2}+W_{3}+W_{4}$
$\mathrm{W}=\mu \mathrm{R} \mathrm{T}_{1} \ln \left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)+\frac{\mu \mathrm{R}}{\gamma-1}\left(\mathrm{~T}_{1}-\mathrm{T}_{2}\right)$
$+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)+\frac{\mu R}{\gamma-1}\left(T_{2}-T_{1}\right)$
$=\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)$
Efficiency of Carnot Engine, $\eta=\frac{W}{Q_{1}}$
$=\frac{\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)}{\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)}$
The points $\mathrm{B}$ and $\mathrm{C}$ are connected by an adiabatic path as are the points $\mathrm{D}$ and $\mathrm{A}$. Hence, using eq. and the adiabatic gas eq.
$\mathrm{T}_{1} \mathrm{~V}_{2}^{(\gamma-1)}=\mathrm{T}_{2} \mathrm{~V}_{3}^{(\gamma-1)}$
And
$\mathrm{T}_{1} V_{1}^{(\gamma-1)}=\mathrm{T}_{2} \mathrm{~V}_{4}^{(\gamma-1)}$
Combination of the above $\mathrm{eq}^{\mathrm{n}}$. gives $\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}=\frac{\mathrm{V}_{3}}{\mathrm{~V}_{4}},$ and, substituting into the ratio of $\mathrm{eq}^{\mathrm{n}}$, we find
$\eta=\frac{T_{1}-T_{2}}{T_{1}}=\frac{Q_{1}-Q_{2}}{Q_{1}}$
$\eta=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}$
$\eta=\frac{T_{1}-T_{2}}{T_{1}} \times 100 \%$
$\eta=\frac{Q_{1}-Q_{2}}{Q_{1}} \times 100 \%$
It can be shown that the efficiency for the Carnot engine is the best that can be obtained for any heat engine and $\mathrm{eq}^{n}$. gives an upper limit to the efficiency of any heat engine operating between temperatures $T_{1}$ and $T_{2}$.
The efficiency depends upon the temperatures $T_{1}$ and $T_{2}$ which approaches un ty only when the temperature of the cold reservoir approaches absolute zero. A steam engine using steam at $373 \mathrm{~K}$ and with the cold reservoir at $273 \mathrm{~K}$ has a best possible efficiency of $\eta \sim 1-(273 / 373) \sim 27 \%$.
The efficiency of a Carnot engine is never $100 \%$ because it is $100 \%$ only if temperature of sink $\mathrm{T}_{2}=0$ which is impossible.
In a Carnot cycle $\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}=\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}}$
or $\frac{Q_{1}}{T_{1}}=\frac{Q_{2}}{T_{2}}$
$\eta_{\mathrm{R}}>\eta_{1}$
Or
$1-\frac{T_{2}}{T_{1}}>1-\frac{Q_{2}}{Q_{1}}$
If you found this article helpful then please share it with your friends.
For a better understanding of this chapter, please check the detailed notes of the Thermodynamics. If you want more Free Learning Videos and Study Material Then don’t forget to download the eSaral Learning App.
Carnot cycle:
Carnot devised an ideal engine that is based on a reversible cycle of four operations in succession: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression.There are four thermodynamical processes isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression.
The main parts of Carnot’s engine are:
Source of Heat: A hot body of high temperature $T_{1}$ from which the heat can be drawn. It is a hot body of very large heat capacity kept at a constant high temperature $T_{1} K$. Its upper surface is perfectly conducting so that the working substance can take heat from heat.Mechanical Arrangements and working substance: A cylinder whose walls are perfectly non-conducting but base perfectly conducting fitted with non-conducting piston which can move without any frictional losses. Ideal gas enclosed in these systems as a working substance.
Heat sink: A cold body at low temperature $\mathrm{T}_{2} \mathrm{~K}$ to which the heat can be rejected. It is a body of large heat capacity. Its upper surface is highly conducting so that the working substance can reject heat to it.
Stand: It is made by perfectly insulating material so that when cylinder placed on it working substance can expended or compressed adiabaticly.
Working: To get maximum work from this type of ideal engine there is a set of reversible processes through then working substance is taken back to the Initial condition. The complete Carnot cycle is divided in four steps.
Processes of Carnot's cycle can be denoted by an indicator diagram a shown here in these diagram variation of pressure (P) and volume (V) of working substance (ideal gas), are plotted.
(a) First process: Isothermal expansion AB
Initially the cyclinder is taken to be in thermal equilbrium with the high temperature $T_{1}$ represented by point $A$
$\left(P_{1}, \quad V_{1}, T_{1}\right)$
This is initial state of working substance (ideal gas)
Then the piston is allowed to move outward s owly. With the
movement of the piston, the temperature of the gas tends to fall. The process is very slow so that it is isothermal. Heat fom reservoir flows into the gas and temperature of the gas remains $\mathrm{T}_{1}$. In this expasion gas receive heat $\mathrm{Q}_{1}$ from source and gets state $\mathrm{B}\left(\mathrm{P}_{2}, \mathrm{~V}_{2}, \mathrm{~T}_{1}\right)$
The total heat input $Q_{1}$ to the gas occurs over the path from $A$ to $B$ and comes from a large reservoir of heat (source) at temperature $\mathrm{T}_{1}$ and utilized for doing work $W_{1}$.
Over the path from A to B the heat input to the gas equals the work done against the external pressure.
$\mathrm{G}_{1}=\int_{\mathrm{V}_{1}}^{\mathrm{V}_{2}} \mathrm{P} \mathrm{d} \mathrm{V}=\int_{\mathrm{V}_{1}}^{\mathrm{V}_{2}} \frac{\mu \mathrm{R} \mathrm{T}_{1}}{\mathrm{~V}}$
$\mathrm{d} \mathrm{V}=\mu \mathrm{R} \mathrm{T}_{1} \ln \left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)$
$W_{1}=\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)$
$\left(W_{1}=Q_{1}\right)$
(b) Second process : adiabatic expansion BC
Now the contact of cylinder with source is removed and cylinder is put in contact with a non-conducting stand. The piston is allowed to move outward the gas now expands adiabatically because no heat can enter in or leave out. The tempeature falls to $\mathrm{T}_{2}$ and gas describes the adiabatic $\mathrm{BC}$ to point $\mathrm{C}\left(\mathrm{P}_{3}, \mathrm{~V}_{3}, \mathrm{~T}_{2}\right)$ during which more work is done $\left(\mathrm{W}_{2}\right)$ at the expense of the internal energy.
Work done over this adiabatic path BC is
$\mathrm{W}_{2}=\frac{\mu \mathrm{R}}{\gamma-1}\left(\mathrm{~T}_{1}-\mathrm{T}_{2}\right)$
(c) Third process : Isothermal compression CD
The gas cylinder is placed in contact with sink at temperature $\mathrm{T}_{2} .$ The piston is moved slowly inward so that heat produced during compression passes to the sink. The gas is isothermally compressed to point D. $\left(P_{4}, V_{4}, T_{2}\right)$
The heat rejected $\mathrm{Q}_{2}$ to the cold reservoir (sink) at $\mathrm{T}_{2}$ occurs over the path from $C$ to $D .$
The amount of work done on the gas $\mathrm{W}_{3}$ is equal to the amount of heat rejected to the sink
$\mathrm{W}_{3}=\mathrm{Q}_{2}$
So that
$\mathrm{W}_{3}=\mu \mathrm{RT}_{2} \ln \left(\frac{\mathrm{V}_{4}}{\mathrm{~V}_{3}}\right)$
or $\mathrm{Q}_{2}=\mu \mathrm{RT}_{2} \ln \left(\frac{\mathrm{V}_{4}}{\mathrm{~V}_{3}}\right)$
(d) Fourth process : Adiabatic compression DA
The cylinder is removed from the sink and is put in contact with insulating stand and piston moves inward. Heat is not allowed to go out and it increases the internal energy of the system. Then work done on the gas during adiabatic compression from state $D$ to initial point $A\left(P_{1}, V_{1}, T_{1}\right)$
No heat exchanges occur over the adiabatic path.
Work done on the system is
$W_{4}=\frac{\mu R}{\gamma-1}\left(T_{2}-T_{1}\right)$
This cycle of operations is called a Carnot cycle. In first two steps work is done by engine $\left(\mathrm{W}_{1}\right.$ and $\mathrm{W}_{2}$ are positive) and in last two steps work is done on gas $\left(\mathrm{W}_{3}\right.$ and $\mathrm{W}_{4}$ are negative)
The work done in complete cylce W is equal to the area of the closed part of the P–V cycle.
$W=W_{1}+W_{2}+W_{3}+W_{4}$
$\mathrm{W}=\mu \mathrm{R} \mathrm{T}_{1} \ln \left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)+\frac{\mu \mathrm{R}}{\gamma-1}\left(\mathrm{~T}_{1}-\mathrm{T}_{2}\right)$
$+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)+\frac{\mu R}{\gamma-1}\left(T_{2}-T_{1}\right)$
$=\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)$
Efficiency of Carnot Engine, $\eta=\frac{W}{Q_{1}}$
$=\frac{\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)+\mu R T_{2} \ln \left(\frac{V_{4}}{V_{3}}\right)}{\mu R T_{1} \ln \left(\frac{V_{2}}{V_{1}}\right)}$
The points $\mathrm{B}$ and $\mathrm{C}$ are connected by an adiabatic path as are the points $\mathrm{D}$ and $\mathrm{A}$. Hence, using eq. and the adiabatic gas eq.
$\mathrm{T}_{1} \mathrm{~V}_{2}^{(\gamma-1)}=\mathrm{T}_{2} \mathrm{~V}_{3}^{(\gamma-1)}$
And
$\mathrm{T}_{1} V_{1}^{(\gamma-1)}=\mathrm{T}_{2} \mathrm{~V}_{4}^{(\gamma-1)}$
Combination of the above $\mathrm{eq}^{\mathrm{n}}$. gives $\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}=\frac{\mathrm{V}_{3}}{\mathrm{~V}_{4}},$ and, substituting into the ratio of $\mathrm{eq}^{\mathrm{n}}$, we find
$\eta=\frac{T_{1}-T_{2}}{T_{1}}=\frac{Q_{1}-Q_{2}}{Q_{1}}$
$\eta=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}$
$\eta=\frac{T_{1}-T_{2}}{T_{1}} \times 100 \%$
$\eta=\frac{Q_{1}-Q_{2}}{Q_{1}} \times 100 \%$
It can be shown that the efficiency for the Carnot engine is the best that can be obtained for any heat engine and $\mathrm{eq}^{n}$. gives an upper limit to the efficiency of any heat engine operating between temperatures $T_{1}$ and $T_{2}$.
The efficiency depends upon the temperatures $T_{1}$ and $T_{2}$ which approaches un ty only when the temperature of the cold reservoir approaches absolute zero. A steam engine using steam at $373 \mathrm{~K}$ and with the cold reservoir at $273 \mathrm{~K}$ has a best possible efficiency of $\eta \sim 1-(273 / 373) \sim 27 \%$.
The efficiency of a Carnot engine is never $100 \%$ because it is $100 \%$ only if temperature of sink $\mathrm{T}_{2}=0$ which is impossible.
In a Carnot cycle $\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}=\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}}$
or $\frac{Q_{1}}{T_{1}}=\frac{Q_{2}}{T_{2}}$
Carnot Theorem
No irreversible engine (I) can have efficiency greater than Carnot reversible engine (R) working between same hot and cold reservoirs i.e.,$\eta_{\mathrm{R}}>\eta_{1}$
Or
$1-\frac{T_{2}}{T_{1}}>1-\frac{Q_{2}}{Q_{1}}$
If you found this article helpful then please share it with your friends.
For a better understanding of this chapter, please check the detailed notes of the Thermodynamics. If you want more Free Learning Videos and Study Material Then don’t forget to download the eSaral Learning App.