As we have studied Coulomb’s Law, we know that charges either attract or repel each other even when they are a distance apart. Have you ever wondered why they experience such a force? It is somewhat like a Tiger. Every charge forms a territory around itself. If some other charge or charges comes in its territory then they experience a force according to their nature. This space a charge creates around itself is called as Electric field.
So, here we are going to know more about Electric Field, its definition and also about electric field intensity in the following order:
Electric field at a point is characterized either by a vector function of position $\mathop E\limits^ \to $ called Electric Field Intensity or by a scalar function of position V called Electric Potential. The electric field in a certain space is also visualized graphically in terms of lines of force. So electric intensity, potential and lines of force are different ways of describing the same field.
[caption id="attachment_4289" align="aligncenter" width="128"]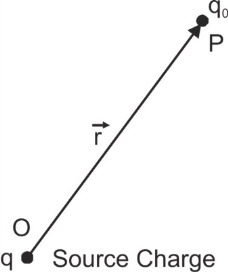
Electric field produced by a point charge[/caption]
If the electric field is produced by a point charge q, then from Coulomb's law $\mathop F\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{q{q_0}} \over {{r^3}}}\mathop r\limits^ \to $ field due to point-charge q at position $\mathop r\limits^ \to $ in free space.
[caption id="attachment_4290" align="aligncenter" width="154"]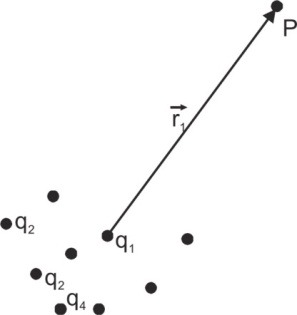
Electric Field produced by charge distributio[/caption]
$\mathop E\limits^ \to = {{\mathop F\limits^ \to } \over {{q_0}}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^3}}}\mathop r\limits^ \to \,\,\,\,or\,\,\,\,E = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}$
If electric field is produced by a charge distribution, then by 'principle of superposition' field is given as
$\mathop E\limits^ \to = \mathop {{E_1}}\limits^ \to + \mathop {{E_2}}\limits^ \to + ....... = \sum\limits_{i = 1}^n {\,\mathop {{E_i}}\limits^ \to } $ with $\mathop {{E_i}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{{q_i}} \over {r_i^3}}\mathop {{r_i}}\limits^ \to $
while for continuous charge distribution (treating small charge element as a point charge),
$d\mathop E\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{dq} \over {r_{}^3}}\mathop r\limits^ \to ,$ i.e., $\mathop E\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}\int {{{dq} \over {{r^3}}}} \mathop r\limits^ \to $
So, here we are going to know more about Electric Field, its definition and also about electric field intensity in the following order:
- Electric Field Definition
- Electric Field Intensity
- Important Points on Electric field
- Examples on Electric Field
Electric Field Definition
To explain 'action at a distance', i.e. 'force without contact' between charges we assume that a charge or charge distribution produces a field in space surrounding it. The region surrounding a charge or charge distribution in which its electrical effects are perceptible is called the electric field of the given charge.Electric field at a point is characterized either by a vector function of position $\mathop E\limits^ \to $ called Electric Field Intensity or by a scalar function of position V called Electric Potential. The electric field in a certain space is also visualized graphically in terms of lines of force. So electric intensity, potential and lines of force are different ways of describing the same field.
Electric Field Intensity $\mathop E\limits^ \to $
The Electric Field Intensity at a point in an Electric Field is defined as the force experienced by a unit positive point charge called test charge supposed to be placed at that point. The test charge does not affect the source charge or charge distribution producing the field. If a test charge q0 at a point P in an electric field experiences a force$\mathop F\limits^ \to $, then electric field$\mathop E\limits^ \to = (\mathop F\limits^ \to /{q_0})$[caption id="attachment_4289" align="aligncenter" width="128"]
Electric field produced by a point charge[/caption]
If the electric field is produced by a point charge q, then from Coulomb's law $\mathop F\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{q{q_0}} \over {{r^3}}}\mathop r\limits^ \to $ field due to point-charge q at position $\mathop r\limits^ \to $ in free space.
[caption id="attachment_4290" align="aligncenter" width="154"]
Electric Field produced by charge distributio[/caption]
$\mathop E\limits^ \to = {{\mathop F\limits^ \to } \over {{q_0}}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^3}}}\mathop r\limits^ \to \,\,\,\,or\,\,\,\,E = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}$
If electric field is produced by a charge distribution, then by 'principle of superposition' field is given as
$\mathop E\limits^ \to = \mathop {{E_1}}\limits^ \to + \mathop {{E_2}}\limits^ \to + ....... = \sum\limits_{i = 1}^n {\,\mathop {{E_i}}\limits^ \to } $ with $\mathop {{E_i}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{{q_i}} \over {r_i^3}}\mathop {{r_i}}\limits^ \to $
while for continuous charge distribution (treating small charge element as a point charge),
$d\mathop E\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{{dq} \over {r_{}^3}}\mathop r\limits^ \to ,$ i.e., $\mathop E\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}\int {{{dq} \over {{r^3}}}} \mathop r\limits^ \to $
Important Points on Electric Field
- It is a vector quantity having dimensions
$E = {F \over q} = {{ML{T^{ - 2}}} \over {AT}} = ML{T^{ - 3}}{A^{ - 1}}$
The SI unit is N/C or V/m as
${N \over C} = {{N \times m} \over {C \times m}}\buildrel {\left( {N \times m = J} \right)} \over \longrightarrow {J \over {C \times m}}\buildrel {\left( {J/C = V} \right)} \over\longrightarrow {V \over m}$ - By definition $\mathop E\limits^ \to = \mathop F\limits^ \to /{q_0},$ or
$\mathop F\limits^ \to = {q_0}\mathop E\limits^ \to $
A charged particle in an electric field experiences a force whether it is at rest or in motion. The direction of force is along the field if it is positive and opposite to the field if it is negative.
- In free space Electric field is ${E_0} = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}$
In a medium of permittivity ε field is
$E = {1 \over {4\pi \varepsilon }}{q \over {{r^2}}}$
So, ${E \over {{E_0}}} = {{{\varepsilon _0}} \over \varepsilon } = {1 \over K}$ [as ε = ε0 K]
Or, E = E0/K - In presence of a dielectric, electric field decreases and becomes 1/K times of its value in free space.The electrostatic field i.e. field produced by charge at rest is conservative.
$F = - {{dU} \over {dr}}$ or ${F \over {{q_0}}} = - {1 \over {{q_0}}}{{dU} \over {dr}}$
or
$E = - {{dV} \over {dr}}$ $\left[ {as{F \over {{q_0}}} = E\,\,and\,\,{U \over {{q_0}}} = V} \right]$ So,
${E_x} = - {{\partial V} \over {\partial x}}$ ${E_y} = - {{\partial V} \over {\partial y}}$ and ${E_z} = - {{\partial V} \over {\partial z}}$ with $\mathop E\limits^ \to = \hat i{E_x} + \hat j{E_y} + \hat k{E_z}$ i.e. if potential V is given $\mathop E\limits^ \to $ can be calculated. - The electric field between two parallel plates separated by a distance d and having a potential difference V, will therefore be given by:$E = - {{dV} \over {dr}} = - {{\left( {{V_2} - {V_1}} \right)} \over {\left( {{r_2} - {r_1}} \right)}} = - {{\left( {0 - V} \right)} \over {\left( {d - 0} \right)}} = {V \over d}$
[caption id="attachment_4292" align="aligncenter" width="197"]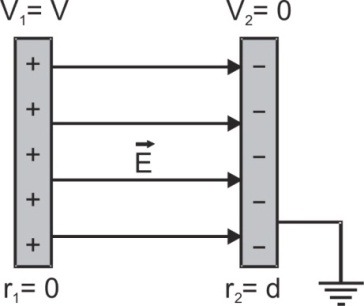
Electric Filed between 2 parallel plates[/caption]
- The value of the electric field has dimensions of force per unit charge. In the meter-kilogram-second and SI systems, the appropriate units are newtons per coulomb, equivalent to volts per meter. In the centimeter-gram-second system, the electric field is expressed in units of dynes per electrostatic unit (esu), equivalent to stat-volts per centimeter. [source]
Solved Examples
Q. A thin spherical conducting shell of radius 'a' carries a charge q. Concentric with it is another thin metallic spherical shell of radius b > a. Calculate electric field at radial distance r when
(a) r < a
(b) a < r < b and
(c) r > b.
What will be the change in the field in above cases if the outer shell
(i) is given a charge Q
(ii) is earthed?
Ans. We know that intensity inside a charged conductor is zero while for external point a charged sphere behaves as if whole of its charge were concentrated at the center, i.e.,
Ein = 0 and ${E_{out}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}$
(a) If r < a, the point A is internal to both the shells, so EA = 0 + 0 = 0
(b) If a < r < b, the point B is external to shell of radius a and internal to shell of radius b, so
${E_B} = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_B^2}} + 0 = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_B^2}}$
(c) If r > b, the point C is external to both the shells and as due to induction –q and +q charges will be induced on the inner and outer surface of spherical shell of radius b,
${E_C} = {1 \over {4\pi {\varepsilon _0}}}{{\left[ {q - q + q} \right]} \over {r_C^2}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_C^2}}$ [< EB as rC > rB]
This all is shown in fig. (A)
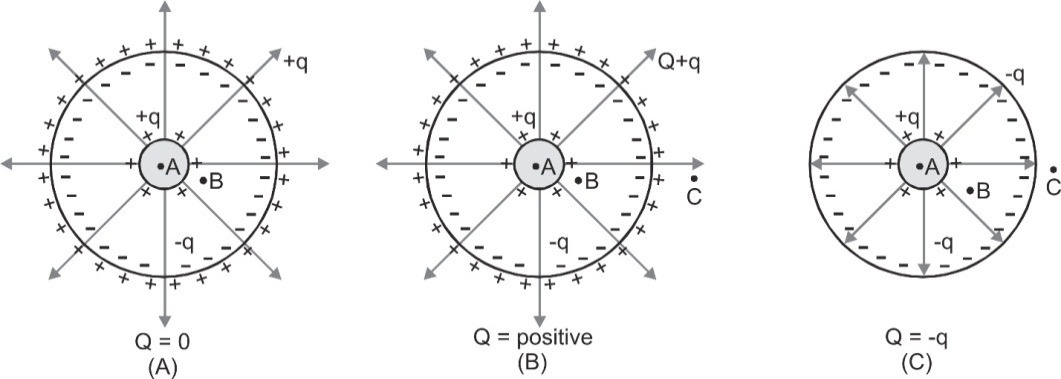
Now if the outer sphere is given a charge Q or is earthed, the result of case (a) and (b) will not change as external charge on a conductor does not affect the field inside it. However, in case (c), i.e., r > b.
(i) If the outer sphere is given a charge Q, the charge Q will also produce electric field so that now:
$E_{C}^{'}={{E}_{C}}+\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{r_{C}^{2}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{(q+Q)}{r_{C}^{2}}$ [> EC]
This is shown in fig. (B).
(ii) If the outer sphere is earthed, the outer sphere will acquire induced charge say q' such that its potential becomes zero as potential of earthed conductor is assumed to be zero then
$V = {1 \over {4\pi {\varepsilon _0}}}{{\left( {q + q'} \right)} \over b} = 0$ i.e., q' = –q
i.e., the induced charge on the outer shell will now be (–q) [and not zero] so now
$E_{C}^{'}={{E}_{C}}+\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{-q}{r_{C}^{2}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{\left( q-q \right)}{r_{C}^{2}}=0$ [< EC]
i.e., field outside the shell is zero. In this situation field exists only in the space between the shells as shown in fig. (C).
Ein = 0 and ${E_{out}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}$
(a) If r < a, the point A is internal to both the shells, so EA = 0 + 0 = 0
(b) If a < r < b, the point B is external to shell of radius a and internal to shell of radius b, so
${E_B} = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_B^2}} + 0 = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_B^2}}$
(c) If r > b, the point C is external to both the shells and as due to induction –q and +q charges will be induced on the inner and outer surface of spherical shell of radius b,
${E_C} = {1 \over {4\pi {\varepsilon _0}}}{{\left[ {q - q + q} \right]} \over {r_C^2}} = {1 \over {4\pi {\varepsilon _0}}}{q \over {r_C^2}}$ [< EB as rC > rB]
This all is shown in fig. (A)
Now if the outer sphere is given a charge Q or is earthed, the result of case (a) and (b) will not change as external charge on a conductor does not affect the field inside it. However, in case (c), i.e., r > b.
(i) If the outer sphere is given a charge Q, the charge Q will also produce electric field so that now:
$E_{C}^{'}={{E}_{C}}+\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{r_{C}^{2}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{(q+Q)}{r_{C}^{2}}$ [> EC]
This is shown in fig. (B).
(ii) If the outer sphere is earthed, the outer sphere will acquire induced charge say q' such that its potential becomes zero as potential of earthed conductor is assumed to be zero then
$V = {1 \over {4\pi {\varepsilon _0}}}{{\left( {q + q'} \right)} \over b} = 0$ i.e., q' = –q
i.e., the induced charge on the outer shell will now be (–q) [and not zero] so now
$E_{C}^{'}={{E}_{C}}+\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{-q}{r_{C}^{2}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{\left( q-q \right)}{r_{C}^{2}}=0$ [< EC]
i.e., field outside the shell is zero. In this situation field exists only in the space between the shells as shown in fig. (C).
Q. A conducting hollow spherical shell having an inner radius ‘a’ and outer radius ‘b’ carries a net charge Q. If a point charge q is placed at the center of this sphere, determine the surface charge density at
(a) the inner surface and
(b) the outer surface.
Ans. If qa and qb are the charges on the inner and outer surfaces of the given shell
${\sigma _a} = {{{q_a}} \over {4\pi {a^2}}}$ and ${\sigma _b} = {{{q_b}} \over {4\pi {b^2}}}$ ---1
The isolated sphere is given a charge Q, so in accordance with conservation of charge
qa + qb = Q ---2
Intensity at a point inside a conductor is zero and external charge does not produce field inside a conductor, so for point P (a < r < b), we have
${E_P} = {1 \over {4\pi {\varepsilon _0}}}{{\left( {q + {q_a}} \right)} \over {{r^2}}} = 0$, i.e., qa = –q
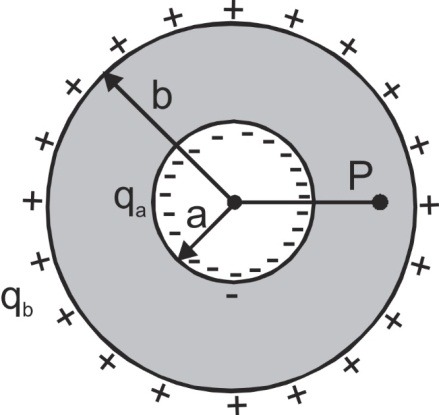So that Eqn. (2) yields qb = Q – qa = Q – (–q) = Q + q
And hence in the light of eqn. (1)
(a) ${\sigma _a} = - {q \over {4\pi {a^2}}}$
and
(b) ${\sigma _b} = {{Q + q} \over {4\pi {b^2}}}$
So that Eqn. (2) yields qb = Q – qa = Q – (–q) = Q + q
And hence in the light of eqn. (1)
(a) ${\sigma _a} = - {q \over {4\pi {a^2}}}$
and
(b) ${\sigma _b} = {{Q + q} \over {4\pi {b^2}}}$
Q. A block having mass m and charge q is resting on a friction-less plane at a distance L from the wall as shown in fig. Discuss the motion of the block when a uniform electric field E is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
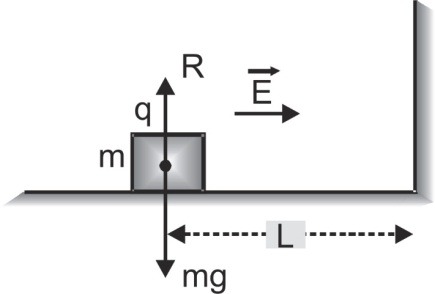
Ans. Electric force $\mathop F\limits^ \to = q\mathop E\limits^ \to $ will accelerate the block towards the wall producing acceleration $a = {F \over m} = {{qE} \over m}$.
As initially the block is at rest and acceleration is constant, so time taken by the block to reach the wall $L = {1 \over 2}a{t^2}$ i.e. $t = \sqrt {{{2L} \over a}} = \sqrt {{{2mL} \over {qE}}} $,
As collision with the wall is perfectly elastic, the block will rebound with same speed and will move in opposite direction. It will come to rest after travelling same distance L in same time t. After stopping it will be again accelerated towards the wall and so the block will execute oscillatory motion with 'span' L and time period $T = 2t = 2\sqrt {{{2mL} \over {qE}}} $
The restoring force F = qE is constant and is not proportional to displacement x, so the motion is not simple harmonic.
Electric field at a point is characterized either by a vector function of position called Electric Field Intensity or by a scalar function of position V called Electric Potential.