Electric lines of Force are used to measure Electric Flux. It is a property of Electric Field which tells us the number of field lines crossing a particular area. It is rate of flow of electric field through a surface which can be open or closed. We will also discuss Gauss’s Law in detail which is an application of Electric Flux which helps to calculate Electric Field for a given charge distribution enclosed by a closed surface. We will study its application in detail here.
Here you will get to know in detail about:
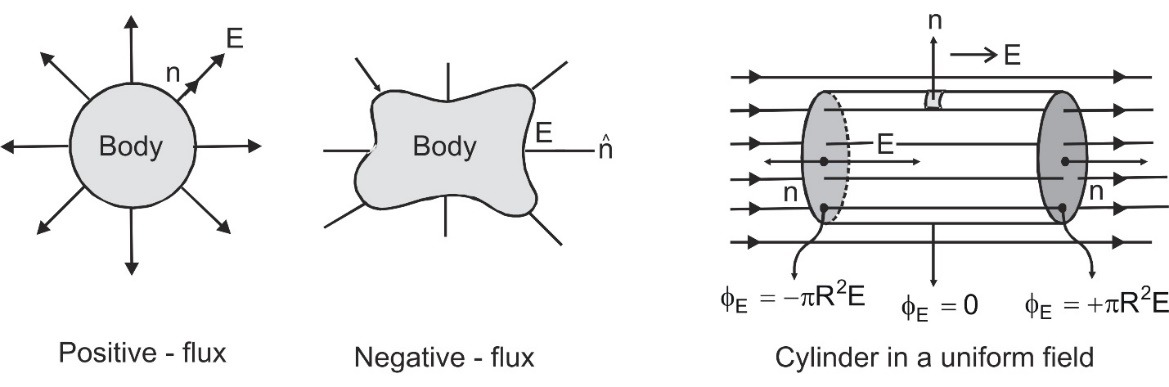 For a closed body outward flux is taken as positive while inward flux is taken as negative[/caption]
For a closed body outward flux is taken as positive while inward flux is taken as negative[/caption]
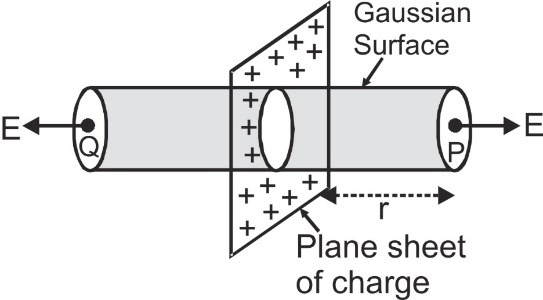 Electric Field due to an infinite plane thin sheet of charge[/caption]
According to gauss law $\oint {\mathop E\limits^ \to .\mathop {dS}\limits^ \to = {q_{in}}/{\varepsilon _0}} $
$\int\limits_{\begin{smallmatrix}I\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}II\,\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}cylindrical \\surface\end{smallmatrix}}{E\,\,ds\cos \theta =}\frac{\sigma A}{{{\varepsilon }_{0}}}$
or EA + EA + 0 = ${{\sigma A} \over {2{\varepsilon _0}}}$
or E =${\sigma \over {2{\varepsilon _0}}}$
Electric Field due to an infinite plane thin sheet of charge[/caption]
According to gauss law $\oint {\mathop E\limits^ \to .\mathop {dS}\limits^ \to = {q_{in}}/{\varepsilon _0}} $
$\int\limits_{\begin{smallmatrix}I\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}II\,\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}cylindrical \\surface\end{smallmatrix}}{E\,\,ds\cos \theta =}\frac{\sigma A}{{{\varepsilon }_{0}}}$
or EA + EA + 0 = ${{\sigma A} \over {2{\varepsilon _0}}}$
or E =${\sigma \over {2{\varepsilon _0}}}$
- Introduction to Electric Flux
- Important Points on Electric Flux
- Gauss’s Law
- Important Points on Gauss’s Law
- Application of Gauss’s Law
- Examples based on Gauss’s Law
Introduction to Electric Flux
Electric flux through an elementary area, ds is defined as the scalar product of area and field, i.e. ${\varphi _{\rm{E}}} = \int {\mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to } $ . It represents the total lines of force passing through the given area. Here area is treated as a vector. The direction of area vector is given by direction of normal to the surface.Important Points on Electric Flux
- It is a real scalar physical quantity with unit volt × m and dimensions
${\varphi _E} = Eds = {F \over q}ds = {{ML{T^{ - 2}}} \over {AT}}{L^2} = M{L^3}{T^{ - 3}}{A^{ - 1}}$
[caption id="attachment_4412" align="aligncenter" width="450"]
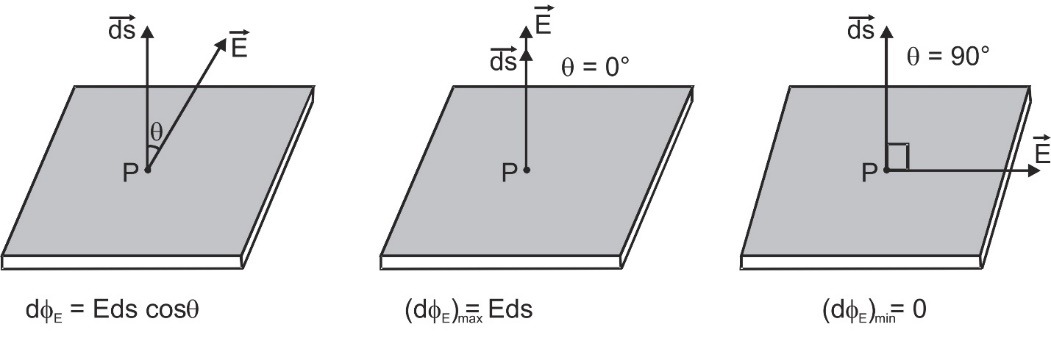 Electric Flux varying with Electric field[/caption]
Electric Flux varying with Electric field[/caption] - It will be maximum when cos θ is max = 1, i.e., θ = 0°, i.e., electric field is normal to the area with (dΦE)max = E ds.
- It will be minimum when cos θ is min = 0, i.e., θ = 90°, i.e. field is parallel to the area with (dΦE)min = 0.
- For a closed body outward flux is taken as positive while inward flux is taken as negative.
 For a closed body outward flux is taken as positive while inward flux is taken as negative[/caption]
For a closed body outward flux is taken as positive while inward flux is taken as negative[/caption]
Gauss's Law
Gauss’s law for electricity states that the electric flux across any closed surface is proportional to the net electric charge enclosed by the surface. The law implies that isolated electric charges exist and that like charges repel one another while unlike charges attract. [source] It relates the total flux of an electric field through a closed surface to the net charge enclosed by that surface. According to it, the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface, Mathematically$\oint\limits_s {\mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to } = {q \over {{\varepsilon _0}}}$Important Points on Gauss’s Law
- Gauss's law and Coulomb's law are equivalent. If we assume Coulomb's law, we can prove Gauss's law and vice versa. To prove Gauss's law from Coulomb's law, consider a hypothetical spherical surface called Gaussian surface of radius r with point charge q at its center. By Coulomb's law intensity at a point P on the surface will be $\mathop E\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^3}}}\mathop r\limits^ \to $ electric flux linked with area $\mathop {ds}\limits^ \to $ $\mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^3}}}\mathop r\limits^ \to \bullet \mathop {ds}\limits^ \to $ direction of $\mathop r\limits^ \to $ and $\mathop {ds}\limits^ \to $ are same i.e., $\mathop r\limits^ \to \bullet \mathop {ds}\limits^ \to $ = r ds cos 0° = r ds. So,$\mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}ds$
or $\oint\limits_s {} \mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to = \oint\limits_s {} {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}ds$
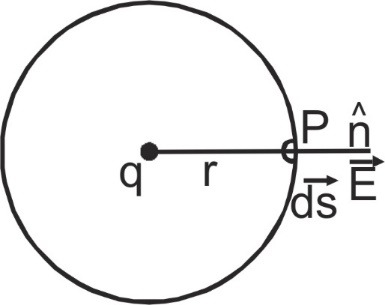 for all points on the sphere r = constant $\oint {} \mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}\oint\limits_s {} ds = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}(4\pi {r^2})$ = ${q \over {{\varepsilon _0}}}$ [as$\oint {ds = 4\pi {r^2}} $] The results are true for any arbitrary surface provided the surface is closed.
for all points on the sphere r = constant $\oint {} \mathop E\limits^ \to \bullet \mathop {ds}\limits^ \to = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}\oint\limits_s {} ds = {1 \over {4\pi {\varepsilon _0}}}{q \over {{r^2}}}(4\pi {r^2})$ = ${q \over {{\varepsilon _0}}}$ [as$\oint {ds = 4\pi {r^2}} $] The results are true for any arbitrary surface provided the surface is closed. - It relates the total flux linked with a closed surface to the charge enclosed by the closed surface:
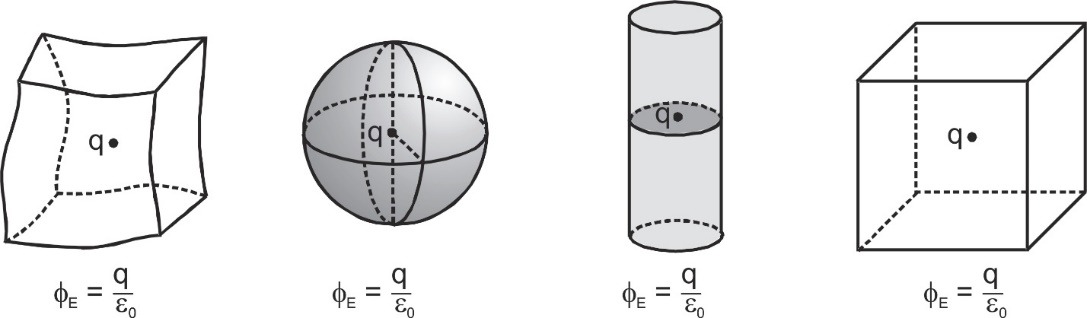
a) If a closed body not enclosing any charge is placed in either uniform on non-uniform electric field total flux linked with it will be zero.
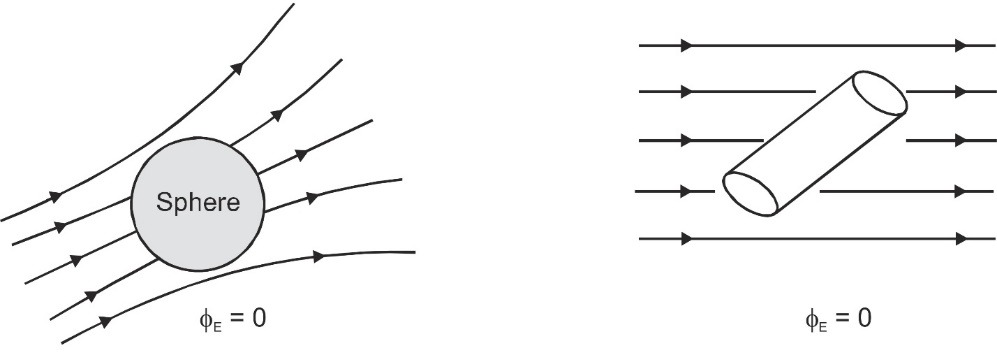 b) If a closed body encloses a charge q, total flux linked with the body is independent of the shape and size of the body and position of charge inside it.
b) If a closed body encloses a charge q, total flux linked with the body is independent of the shape and size of the body and position of charge inside it.

Applications of Gauss’s Law
Electric Field due to a line charge:
Gauss law is useful in calculating electric field intensity due to symmetrical charge distributions. We consider a gaussian surface which is a cylinder of radius r which encloses a line charge of length h with line charge density λ. According to Gauss law $\oint {\mathop E\limits^ \to .\mathop {ds}\limits^ \to } $=${{{q_{in}}} \over {{\varepsilon _0}}}$ $\begin{align}& \int{\overset{\to }{\mathop{E}}\,.\overset{\to }{\mathop{ds}}\,} \\ & Cylindrical \\ & surface \\ \end{align}$+$\begin{align}& \int{\overset{\to }{\mathop{E}}\,.\overset{\to }{\mathop{ds}}\,} \\ & \,circular \\ & surface \\\end{align}$+$\begin{align}& \int{\overset{\to }{\mathop{E}}\,.\overset{\to }{\mathop{ds}}\,} \\ & \,circular \\ & surface \\\end{align}$=$\frac{\lambda h}{{{\varepsilon }_{0}}}$ $\begin{align}&\int{Eds\,\,\cos \,\,0{}^\text{o}} \\& Cylindrical \\& suface \\\end{align}$+$\begin{align}& \int{Eds\,\,\cos } \\& I\,circular \\& surface \\\end{align}$$\frac{\pi }{2}$+$\begin{align}& \int{Eds\,\,\cos } \\& II\,circular \\& surface \\\end{align}$$\frac{\pi }{2}$=$\frac{\lambda h}{{{\varepsilon }_{0}}}$ E(2 πr h) =$\frac{\lambda h}{{{\varepsilon }_{0}}}$ So, E = $\frac{\lambda }{2\ \pi \ {{\varepsilon }_{0}}\ r}$$(E\propto \frac{1}{r})$Electric Field due to an infinite plane thin sheet of charge:
To find electric field due to the plane sheet of charge at any point P distant r from it, choose a cylinder of area of cross-section A through the point P as the Gaussian surface. The flux due to the electric field of the plane sheet of charge passes only through the two circular caps of the cylinder. Let surface charge density = σ [caption id="attachment_4418" align="aligncenter" width="242"] Electric Field due to an infinite plane thin sheet of charge[/caption]
According to gauss law $\oint {\mathop E\limits^ \to .\mathop {dS}\limits^ \to = {q_{in}}/{\varepsilon _0}} $
$\int\limits_{\begin{smallmatrix}I\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}II\,\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}cylindrical \\surface\end{smallmatrix}}{E\,\,ds\cos \theta =}\frac{\sigma A}{{{\varepsilon }_{0}}}$
or EA + EA + 0 = ${{\sigma A} \over {2{\varepsilon _0}}}$
or E =${\sigma \over {2{\varepsilon _0}}}$
Electric Field due to an infinite plane thin sheet of charge[/caption]
According to gauss law $\oint {\mathop E\limits^ \to .\mathop {dS}\limits^ \to = {q_{in}}/{\varepsilon _0}} $
$\int\limits_{\begin{smallmatrix}I\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}II\,\,circular \\surface\end{smallmatrix}}{E\,\,ds\cos \theta+}\int\limits_{\begin{smallmatrix}cylindrical \\surface\end{smallmatrix}}{E\,\,ds\cos \theta =}\frac{\sigma A}{{{\varepsilon }_{0}}}$
or EA + EA + 0 = ${{\sigma A} \over {2{\varepsilon _0}}}$
or E =${\sigma \over {2{\varepsilon _0}}}$
Points to remember
- The magnitude of the electric field due to the infinite plane sheet of charge is independent of the distance from the sheet.
- If the sheet is positively charged, the direction of the field is normal to the sheet and directed outward on both sides. But for a negatively charged sheet, the field is directed normally inwards on both sides of the sheet.
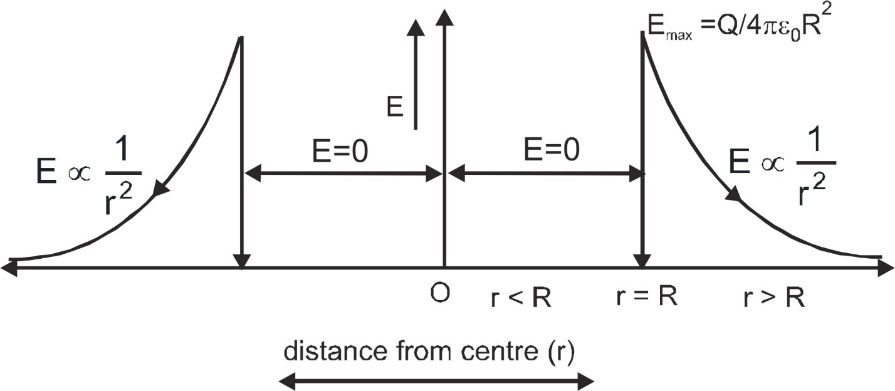
Electric Field Intensity due to uniformly charged spherical shell:
We consider a thin shell of radius R carrying a charge Q on its surface- At a point P0 outside the shell (r > R)
[caption id="attachment_4421" align="aligncenter" width="168"]
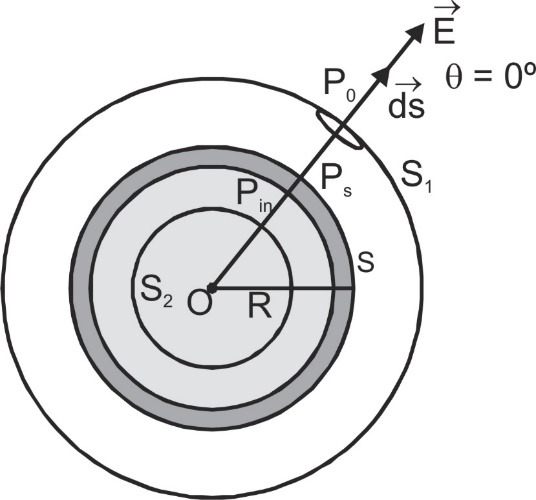 Gauss's Law at a point outside the shell (r > R)[/caption]
According to gauss law $\oint\limits_{{S_1}} {\mathop {{E_0}}\limits^ \to .\mathop {ds}\limits^ \to } $ = ${Q \over {{\varepsilon _0}}}$ or E0 (4πr2) =${Q \over {{\varepsilon _0}}}$
E0 = ${Q \over {4\;\pi \;{\varepsilon _0}{r^2}}}$ = ${\sigma \over {{\varepsilon _0}}}$${{{R^2}} \over {{r^2}}}$
where the surface charge density σ = ${{total\,\,ch\arg e} \over {surface\,\,area}}$ = ${Q \over {4\pi {R^2}}}$
The electric field at any point outside the shell is same as if the entire charge is concentrated at center of shell.
Gauss's Law at a point outside the shell (r > R)[/caption]
According to gauss law $\oint\limits_{{S_1}} {\mathop {{E_0}}\limits^ \to .\mathop {ds}\limits^ \to } $ = ${Q \over {{\varepsilon _0}}}$ or E0 (4πr2) =${Q \over {{\varepsilon _0}}}$
E0 = ${Q \over {4\;\pi \;{\varepsilon _0}{r^2}}}$ = ${\sigma \over {{\varepsilon _0}}}$${{{R^2}} \over {{r^2}}}$
where the surface charge density σ = ${{total\,\,ch\arg e} \over {surface\,\,area}}$ = ${Q \over {4\pi {R^2}}}$
The electric field at any point outside the shell is same as if the entire charge is concentrated at center of shell. - At a point Ps on surface of shell (r = R) ES = ${Q \over {4\pi {\varepsilon _0}{R^2}}}$ = ${\sigma \over {{\varepsilon _0}}}$
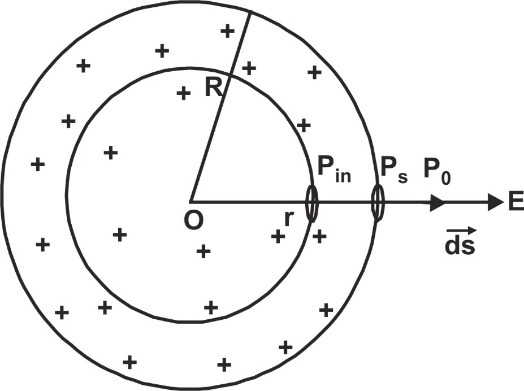
- At a point Pin inside the shell (r < R)
[caption id="attachment_4424" align="aligncenter" width="427"]
 Gauss's Law at a point inside the shell (r < R)[/caption]
According to gauss law $\oint\limits_{{S_2}} {\mathop E\limits^ \to .\mathop {ds}\limits^ \to } $ = ${{{q_{in}}} \over {{\varepsilon _0}}}$. As enclosed charge qin = 0.
So, Ein = 0.
The electric field inside the spherical shell is always zero.
Gauss's Law at a point inside the shell (r < R)[/caption]
According to gauss law $\oint\limits_{{S_2}} {\mathop E\limits^ \to .\mathop {ds}\limits^ \to } $ = ${{{q_{in}}} \over {{\varepsilon _0}}}$. As enclosed charge qin = 0.
So, Ein = 0.
The electric field inside the spherical shell is always zero.
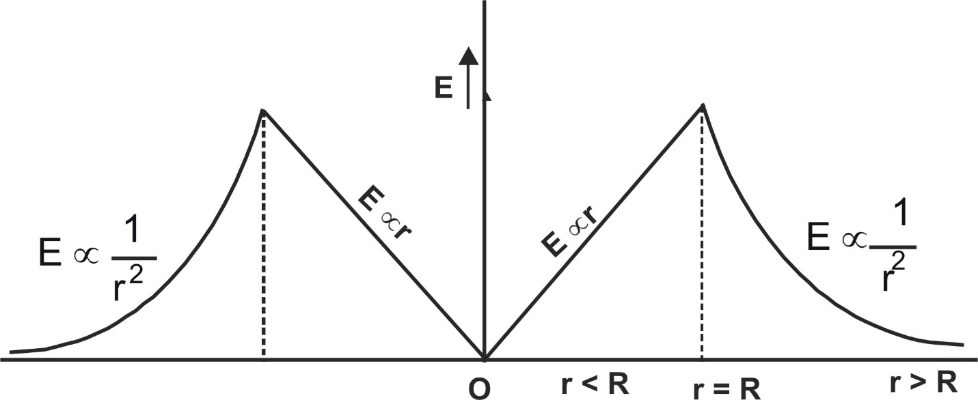
Electric field intensity due to a spherical uniformly charge distribution:
We consider a spherical uniformly charge distribution of radius R in which total charge Q is uniformly distributed throughout the volume. The charge density ρ= ${{total\,\,ch\arg e} \over {total\,\,volume}}$ = ${Q \over {{4 \over 3}\pi {R^3}}}$ = ${{3Q} \over {4\pi {R^3}}}$- At a point P0 outside the sphere (r > R)
According to gauss law $\oint {{{\mathop E\limits^ \to }_0}.\mathop {ds}\limits^ \to } $ = ${Q \over {{\varepsilon _0}}}$ or E0 (4πr2) = ${Q \over {{\varepsilon _0}}}$
or E0 = ${Q \over {4\;\pi \;{\varepsilon _0}{r^2}}}$ = ${\rho \over {3\;{\varepsilon _0}}}$$\left( {{{{R^3}} \over {{r^2}}}} \right)$
[caption id="attachment_4427" align="aligncenter" width="239"]
 Gauss's Law at a point outside the sphere (r > R)[/caption]
Gauss's Law at a point outside the sphere (r > R)[/caption] - At a point Ps on surface of sphere (r = R) Es =${Q \over {4\pi \;{\varepsilon _0}{R^2}}}$ = ${\rho \over {3{\varepsilon _0}}}$ R
- At a point Pin inside the sphere (r < R)
According to Gauss law,
[caption id="attachment_4430" align="aligncenter" width="362"]
 Gauss's Law at a point inside the sphere (r < R)[/caption]
$\oint {{{\mathop E\limits^ \to }_{in}}.\mathop {ds}\limits^ \to } $=${{{q_{in}}} \over {{\varepsilon _0}}}$=${1 \over {{\varepsilon _0}}}$ ρ. ${4 \over 3}$πr3 = ${{Q{r^3}} \over {{\varepsilon _0}{R^3}}}$
Ein(4πr2) =${{Q{r^3}} \over {{\varepsilon _0}{R^3}}}$
or Ein = ${{Qr} \over {4\pi \;{\varepsilon _0}{R^3}}}$ = ${\rho \over {3{\varepsilon _0}}}$ r (Ein ∝ r)
Gauss's Law at a point inside the sphere (r < R)[/caption]
$\oint {{{\mathop E\limits^ \to }_{in}}.\mathop {ds}\limits^ \to } $=${{{q_{in}}} \over {{\varepsilon _0}}}$=${1 \over {{\varepsilon _0}}}$ ρ. ${4 \over 3}$πr3 = ${{Q{r^3}} \over {{\varepsilon _0}{R^3}}}$
Ein(4πr2) =${{Q{r^3}} \over {{\varepsilon _0}{R^3}}}$
or Ein = ${{Qr} \over {4\pi \;{\varepsilon _0}{R^3}}}$ = ${\rho \over {3{\varepsilon _0}}}$ r (Ein ∝ r)
Example based on Gauss’s Law
Q.It has been experimentally observed that the electric field in a large region of earth's atmosphere is directed vertically down. At an altitude of 300 m, the electric field is 60 Vm–1. At an altitude of 200m, the field is 100 Vm–1. Calculate the net amount of charge contained in the cube of 100 m edge, located between 200m and 300m altitude.
Ans.According to Gauss's theorem, electric flux: ${\varphi _E} = {q \over {{\varepsilon _0}}} = \int {\mathop E\limits^ \to .\mathop {dS}\limits^ \to } $
The surface integral in the above equations contains six terms – the surface integral over the bottom surface, the surface integral over the top surface and surface integral over the four vertical faces.
For the bottom surface, both the vectors and are in the same direction. For the top surface, they act in opposite directions while for the vertical faces, they are perpendicular to each other.
Hence,${\varphi _E} = \int\limits_{bottom} {\mathop {{E_1}}\limits^ \to .\mathop {dS}\limits^ \to } + \int\limits_{top} {\mathop {{E_2}}\limits^ \to .\mathop {dS}\limits^ \to } + 4\int\limits_{vertical} {\mathop E\limits^ \to .\mathop {dS}\limits^ \to } $
$ = \int\limits_{{\rm{bottom}}} {{{\rm{E}}_{\rm{1}}}{\rm{ dS cos 0}}^\circ } + \int\limits_{{\rm{top}}} {{{\rm{E}}_{\rm{2}}}{\rm{ dS cos 180}}^\circ } + {\rm{4}}\int\limits_{{\rm{vertical}}} {{\rm{E dS cos 90}}^\circ } $
$ = \int\limits_{{\rm{bottom}}} {{{\rm{E}}_{\rm{1}}}{\rm{ dS}}} - \int\limits_{{\rm{top}}} {{{\rm{E}}_{\rm{2}}}{\rm{ dS }}} = {E_1}S - {E_2}S = \left( {{E_1} - {E_2}} \right)S$
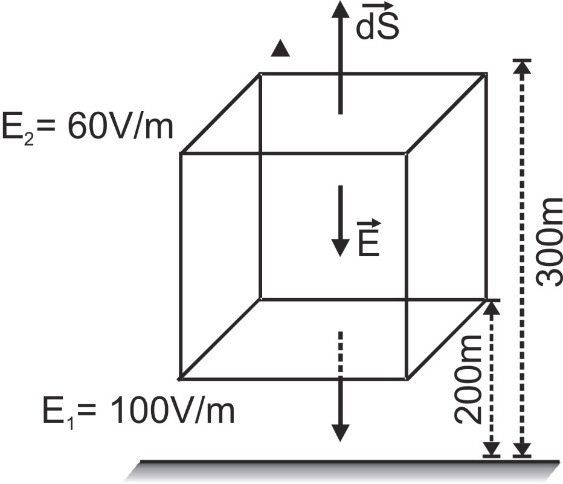 Also, ΦE = q/ε0
∴q = ε0(E1 – E2)S = (8.85 × 10–12 C2 N–1 m–2) (100 V/m – 60 V/m) (100 m2) = 3.54 × 10–6 C
Also, ΦE = q/ε0
∴q = ε0(E1 – E2)S = (8.85 × 10–12 C2 N–1 m–2) (100 V/m – 60 V/m) (100 m2) = 3.54 × 10–6 C
 Also, ΦE = q/ε0
∴q = ε0(E1 – E2)S = (8.85 × 10–12 C2 N–1 m–2) (100 V/m – 60 V/m) (100 m2) = 3.54 × 10–6 C
Also, ΦE = q/ε0
∴q = ε0(E1 – E2)S = (8.85 × 10–12 C2 N–1 m–2) (100 V/m – 60 V/m) (100 m2) = 3.54 × 10–6 C
Q.The charge density of a uniformly charged metallic plate is σ = – 2μC/m2. Find the distance from which a 50eV electron must be projected so that it does not strike the plate.
Ans.The electric field due to metallic sheet $\mathop E\limits^ \to $=${\sigma \over {{\varepsilon _0}}}$$\hat n$= K(4)$\hat n$
where $\hat n$ is unit vector perpendicular to plate
$\mathop E\limits^ \to $ = 9 × 109 × 4 × π(–2 × 10–6) $\hat n$ = 72π× 103 (–$\hat n$) N/C
Force on electron due to this field $\mathop F\limits^ \to $ = $\mathop {qE}\limits^ \to $ = 72π× 10+3 (– 1.6 × 10–19) (–$\hat n$)
= 72× 1.6 × π× 10–16$\hat n$
Let electron be left from a distance d then F.d = energy of electron
or 72 × 1.6 × π× 10–16 × d = 50 × 1.6 × 10–19 or d = 0.221 × 10–3 m
Q.If a point charge q is placed at the center of a cube what is the flux linked
(a) with the cube and
(b) with each face of the cube?
Ans.(a) According to Gauss's law flux linked with a closed body is 1/ε0 times the charge enclosed and here the closed body cube is enclosing a charge q so, ${\varphi _T} = {q \over {{\varepsilon _0}}}$ .
(b) Now as cube is a symmetrical body with 6-faces and the point charge is at its center, so electric flux linked with each face will be${\varphi _F} = {1 \over 6}\left( {{\varphi _T}} \right) = {q \over {6{\varepsilon _0}}}$ .
Q.If a point charge q is placed at one corner of a cube, what is the flux linked with the cube?
Ans.In this case by placing three cubes at three sides of given cube and four cubes above, the charge will be in the center, So, the flux linked with each cube will be one-eighth of the flux q/ε0.
Flux associated with given cube =${q \over {8{\varepsilon _0}}}$ .
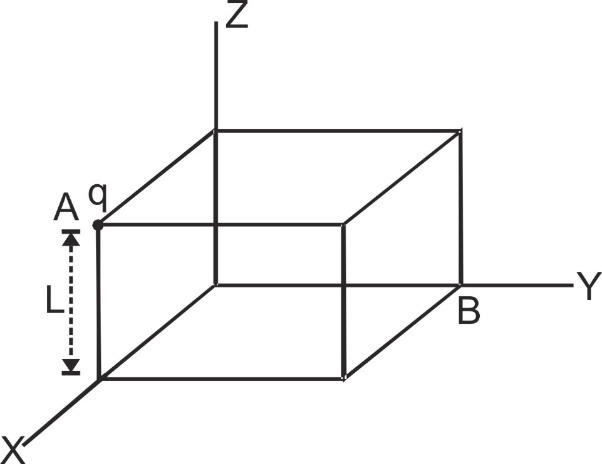
Q.A point charge q is placed at one corner of a cube of edge a. What is the flux through each face of the cube?
Ans.At a corner, 8 cubes can be placed symmetrically, flux linked with each cube due to a charge q at the corner will be q/8ε0
For the faces passing through the edge A, electric field E will be parallel to area of face and so flux through these three faces will be zero.
As the cube has six faces and flux linked with three faces (through A) is zero, so flux linked with remaining three face will be (q/8ε0). The remaining three faces are symmetrical so flux linked with each of the three faces passing through B will be,$ = {1 \over 3} \times \left[ {{1 \over 8}\left( {{q \over {{\varepsilon _0}}}} \right)} \right] = {1 \over {24}}{q \over {{\varepsilon _0}}}$