eSaral provides chemistry short notes for JEE and NEET to help students in revising topics quickly. These notes are completely based on latest syllabus and it includes all the tips and tricks that will help you in learning chemistry better and score well.
The Notes will help you to understand the important topics and remember the key points for exam point of view.
You can also access detailed Notes of chemistry here.
Download or View Detailed Notes for Chemistry Class 11th
Download or View Detailed Notes for Chemistry Class 12th
Electrochemical cells
An electrochemical cell consists of two electrodes (metallic conductors) in contact with an electrolyte (an ionic conductor).
An electrode and its electrolyte comprise an Electrode Compartment. Electrochemical Cells can be classified as:
(i) Electrolytic Cells in which a nonspontaneous reaction is driven by an external source of current.
(ii) Galvanic Cells which produce electricity as a result of a spontaneous cell reaction
Note : In a galvanic cell, cathode is positive with respect to anode.In a electrolytic cell, anode is made positive with respect to cathode.
Electrolysis
The decomposition of electrolyte solution by passage of electric current, resulting into deposition of metals or liberation of gases at electrodes is known as electrolysis.
Electrolytic Cell
This cell converts electrical energy into chemical energy. The entire assembly except that of the external battery is known as the electrolytic cell
Electrodes
The metal strip at which positive current enters is called anode; anode is positively charged in electrolytic cell. On the other hand, the electrode at which current leaves is called cathode. Cathodes are negatively charged.
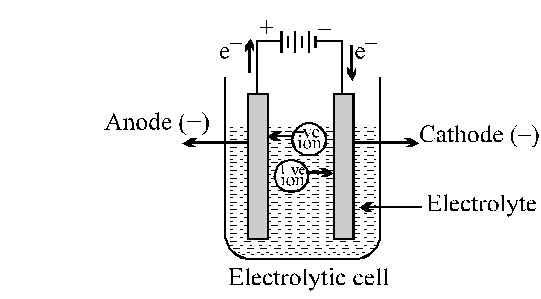
Electrolysis of Molten sodium chloride
$\mathrm{NaCl}(\mathrm{molten}) \longrightarrow \mathrm{Na}^{+}+\mathrm{Cl}^{-}$
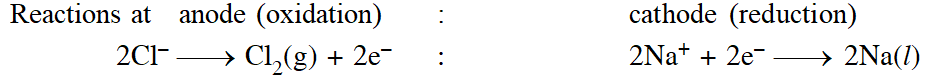There are two types of electrodes used in the electroytic cell, namely attackable and non - attackable. The attackable elecrodes participitate in the electrode reaction. They are made up of reactive metals like Zn, Cu, Ag etc. In such electrodes, atom of the metal gets oxidised into the corresponding cation, which is passed into the solution. Thus, such anodes get dissolved and their mass decreases. On the other hand, non-attackable electrodes do not participiate in the electrode reaction as they made up of unreactive elements like Pt, graphite etc. Such electrodes do not dissolve and their mass remain same.
Faraday’s laws of electrolysis:
(i) First law of electrolysis :
Amount of substance deposited or liberated at an electrode is directly proportional to amount of charge passed (utilized) through the solution.
$\mathrm{w} \propto \mathrm{Q}$
W = weight liberated, Q = charge in coulomb
w = ZQ
Z = electrochemical equivalent
when Q = 1 coulomb, then w = Z
Thus, weight deposited by 1 coulomb charge is called electrochemical equivalent.
Let 1 ampere current is passed till ‘t’ seconds .
Then, Q = It w = ZIt
1 Faraday = 96500 coulomb = Charge of one mole electrons
One faraday is the charge required to liberate or deposit one gm equivalent of a substance at corresponding electrode.
Let ‘E’ is equivalent weight then ‘E’ gm will be liberated by 96500 coulomb.
$\therefore 1$ Coulomb will liberate $\frac{\mathrm{E}}{96500} \mathrm{gm} ;$ By definition, $Z=\frac{\mathrm{E}}{96500}$
$\therefore W=\frac{I t E}{96500}$
When a gas is evolved at an electrode, then above formula changes as,
$\mathrm{V}=\frac{\mathrm{ItV}_{\mathrm{e}}}{96500}$
where V = volume of liberated gas, $\mathrm{V}_{\mathrm{e}}$ = equivalent volume of gas.
Equivalent volume may be defined as:
The volume of gas liberated by 96500 coulomb at STP.
(ii) Second law of electrolysis :
When same amount of charge is passed through different electrolyte solutions connected in series then weight of substances deposited or dissolved at anode or cathode are in ratio of their equivalent weights. i.e.
$\mathrm{w}_{1} / \mathrm{w}_{2}=\mathrm{E}_{1} / \mathrm{E}_{2}$
QUALITATIVE ASPECTS OF ELECTROLYSIS
In the electrolysis process we have discussed above, we have taken molten salt as electrolyte, which contains only one cation and anion. Now, if the electrolyte taken contains more than one cation and anion (for example, aqueous solution of the ionic electrolyte), then the cation and anion that will get discharged depends on the ability of cation to get reduced and the ability of anion to get oxidised.
The ability of an ion to get oxidised or reduced depends upon the size, mass, positive charge, negative charge etc. Thus, it is not possible to predict qualitatively that which ion would be discharged first, a one factor might enhance the ability to discharge while the other factor may hamper it. This can only be predicted on the basis of quantitative value assigned based on the cumulative effect of all the factors reponsible for an ion's ability to discharge. The value is referred as standard potential, which is determined by keeping the concentration of ion as 1 M, pressure of gas at 1 atm, and the measurement done at $25^{\circ} \mathrm{C}$. For a cation, the standard reduction potential (SRP) values are compared. The cation having higher standard reduction potential value is discharged in preference to cation with lower SRP value provided the ions are at 1 M concentration. For an anion, the standard oxidation potential (SOP) values are compared and anion having higher SOP is preferentially discharged, if the concentration is 1 M for each of the ion. The SRP values at $25^{\circ} \mathrm{C}$for some of the reduction half reactions are given in the table below.
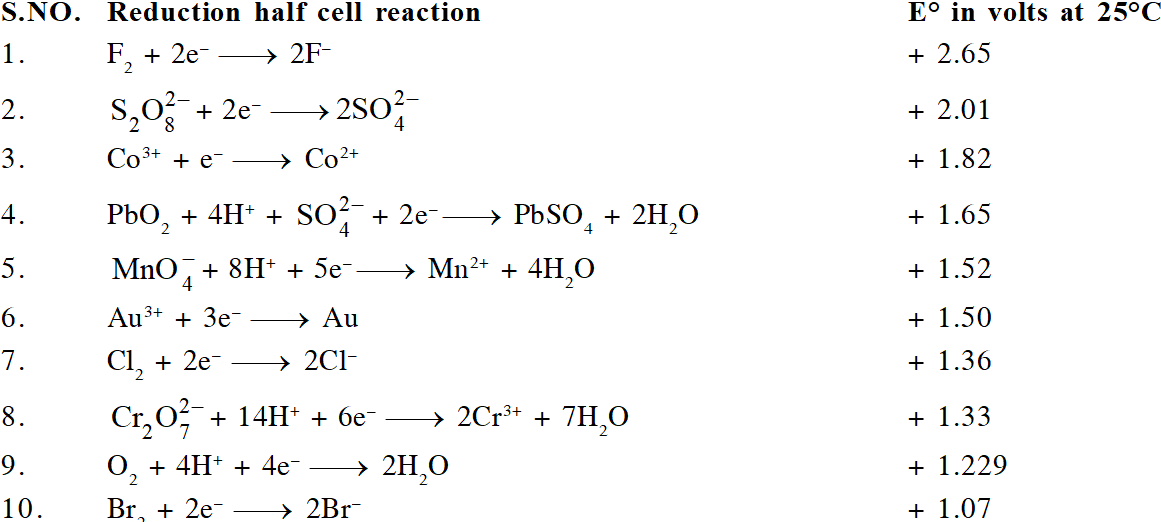
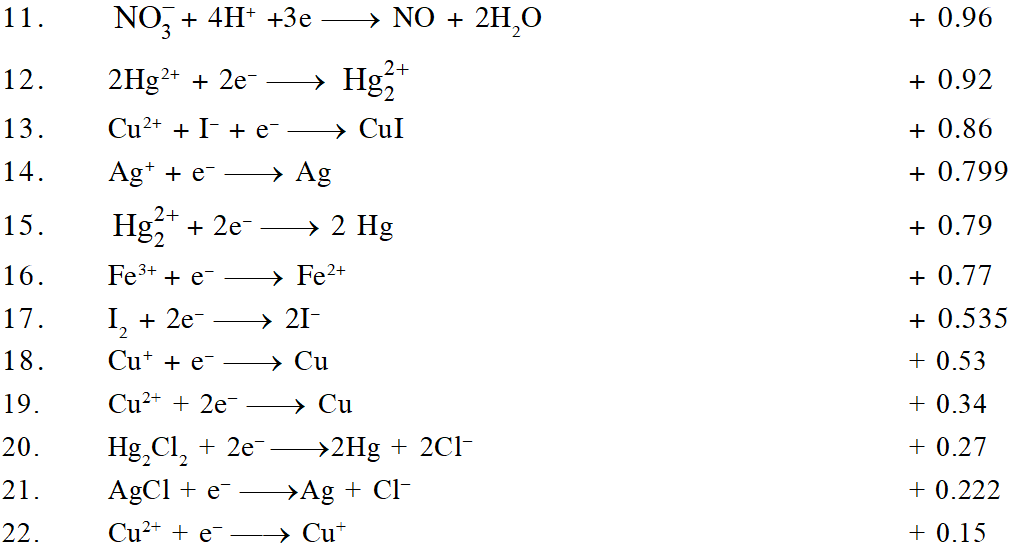
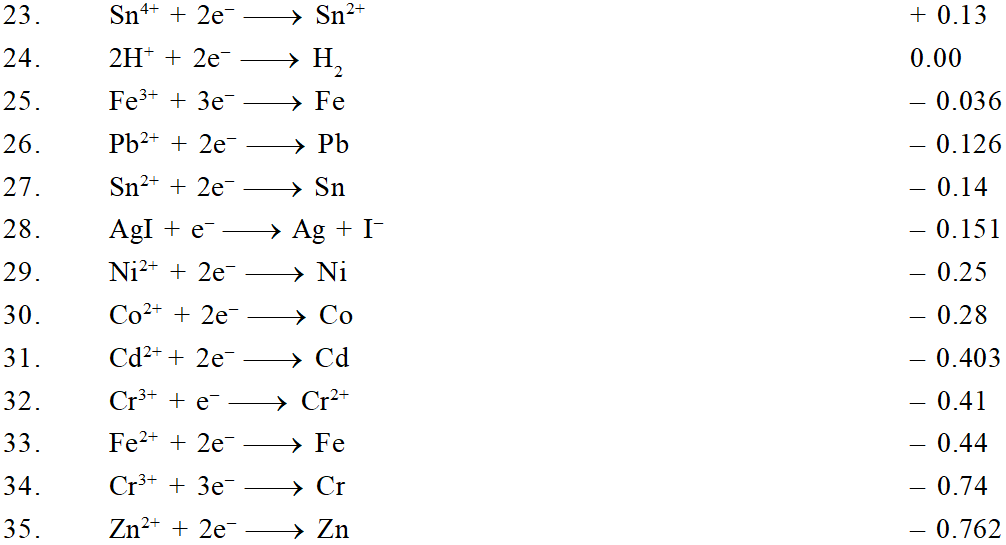
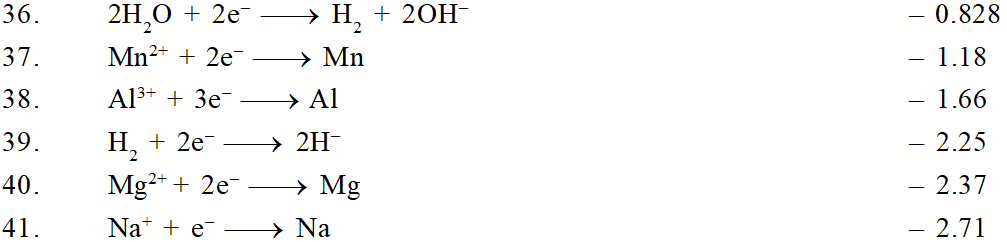
When solution of an electroyte contains more than one type of cations and anions at concentrations different than 1 M, the discharge of an ion does not depend solely on standard potentials but also depends on the concentration of ion in the solution. This value is refered as potential, called as reduction potential for cation and oxidation potential for anion. The relation between reduction potential and standard reduction potential is given by Nernst equation, as
$\mathrm{E}_{\mathrm{RP}}=\mathrm{E}_{\mathrm{RP}}^{\circ}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln \frac{[\text { concentration of product }]}{[\text { concentration of reac tan } \mathrm{t}]}$
where $E_{R P}$ = Reduction potential of cation and $\mathrm{E}^{\mathrm{O}} \mathrm{RP}$= Standard reduction potential of cation.
Thus, it is possible that a cation (A+) with lower standard reduction potential getting discharged in preference to cation $\left(\mathrm{B}^{+}\right)$ having higher standard reduction potential because their concentration might be such that the reduction potential of $\mathrm{A}^{+}$ is higher than that of $\mathrm{B}^{+}$.
When two metal ions in the solution have identical values of their reduction potentials, the simultaneous deposition of both the metals will occur in the form of an alloy.
Galvanic Cell
This cell converts chemical energy into electrical energy.
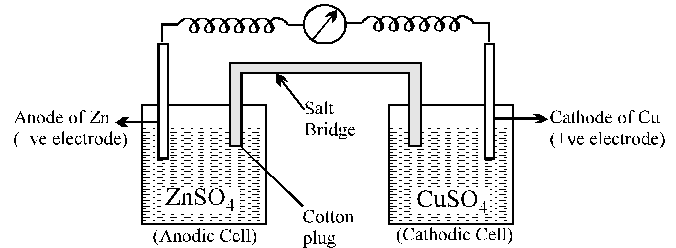Galvanic cell is made up of two half cells i.e., anodic and cathodic. The cell reaction is of redox kind. Oxidation takes place at anode and reduction at cathode. It is also known as voltaic cell. It may be represented as shown in Fig. Zinc rod immersed in $\mathrm{ZnSO}_{4}$ behaves as anode and copper rod immersed in $\mathrm{CuSO}_{4}$ behaves as cathode.
Oxidation takes place at anode:
$\mathrm{Zn}^{3 / 4} \rightarrow \mathrm{Zn}^{2+}+2 \mathrm{e}^{-}$ (loss of electron : oxidation)
Reduction takes place at cathode:
$\mathrm{Cu}^{2+}+2 \mathrm{e}^{-} \longrightarrow \mathrm{Cu}(\text { gain of electron } ; \text { reduction })$
Over all process:
$\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+} \longrightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}$
In galvanic cell like Daniell cell; electrons flow from anode (zinc rod) to the cathode (copper rod) through external circuit; zinc dissolves as $\mathrm{Zn}^{2+} ; \mathrm{Cu}^{2+}$ion in the cathode cell picks up two electron and become deposited at cathode.
Salt Bridge
Two electrolyte solutions in galvanic cells are seperated using salt bridge as represented in the Fig. salt bridge is a device to minimize or eliminate the liquid junction potential. Saturated solution of salt like KCI, $\mathrm{KNO}_{3}$, $\mathrm{NH}_{4} \mathrm{Cl}$ and $\mathrm{NH}_{4} \mathrm{NO}_{3}$ etc. in agar-agar gel is used in salt bridge. Salt bridge contains high concentration of ions viz. $\mathrm{K}^{+}$ and $\mathrm{NO}_{3}^{-}$at the junction with electrolyte solution. Thus, salt bridge carries whole of the current across the boundary ; more over the $\mathrm{K}^{+}$ and $\mathrm{NO}_{3}^{-}$ ions have same speed. Hence, salt bridge with uniform and same mobility of cations and anions minimize the liquid junction potential & completes the electrical circuit & permits the ions to migrate.
Representation of a cell (IUPAC conventions ): Let us illustrate the convention taking the example of Daniel cell.
(i) Anodic half cell is written on left and cathodic half cell on right hand sid
$\mathrm{Zn}(\mathrm{s})\left|\mathrm{ZnSO}_{4}(\mathrm{sol}) \| \mathrm{CuSO}_{4}(\mathrm{sol})\right| \mathrm{Cu}(\mathrm{s})$
(ii) Two half cells are separated by double vertical lines: Double vertical lines indicate salt bridge or any type of porous partition.
(iii) EMF (electromotive force) may be written on the right hand side of the cell.
(iv) Single vertical lines indicate the phase separation between electrode and electrolyte solution.
$\mathrm{Zn}\left|\mathrm{Zn}^{2+} \| \mathrm{Cu}^{2+}\right| \mathrm{Cu}$
Concept of Electromotive force (EMF) of a Cell
Electron flows from anode to cathode in external circuit due to a pushing effect called or electromotic force (e.m.f.). E.m.f. is some times called as cell potential. Unit of e.m.f. of cell is volt.
EMF of cell may be calculated as :
$E_{\operatorname{cell}}$ reduction potential of cathode - Reduction potential of anode
Similarly, standard e.m.f. of the cell $\left(\mathrm{E}^{\circ}\right)$ may be calculated as
$\mathrm{E}_{\text {cell }}^{\circ}$ = Standard reduction potential of cathode - Standard reduction potential of anode
Sign Convention of EMF
EMF of cell should be positive other wise it will not be feasible in the given direction .
$\begin{array}{ll}{\mathrm{Zn}\left|\mathrm{ZnSO}_{4} \| \mathrm{CuSO}_{4}\right| \mathrm{Cu}} & {\mathrm{E}=+1.10 \text { volt } \quad \text { (Feasible) }} \\ {\mathrm{Cu}\left|\mathrm{CuSO}_{4} \| \mathrm{ZnSO}_{4}\right| \mathrm{Zn}} & {\mathrm{E}=-1.10 \text { volt } \quad \text { (Not Feasible) }}\end{array}$
Nernst Equation
Walter Nernst derived a relation between cell potential and concentration or Reaction quotient.
$\Delta \mathrm{G}=\Delta \mathrm{G}^{\circ}+\mathrm{R} \mathrm{T} \ln \mathrm{Q}$ $\ldots .(1)$
where $\Delta \mathrm{G}$ and $\Delta \mathrm{G}^{\circ}$are free energy and standard free energy change; ‘Q’ is reaction quotient.
Let n, Faraday charge is taken out from a cell of e.m.f. (E) then electrical work done by the cell may be calculated as,
Work done = Charge x Potential = nFE
From thermodynamics we know that decrease in Gibbs free energy of a system is a measure of reversible or maximum obtainable work by the system if there is no work due to volume expans
$\therefore-\Delta \mathrm{G}=n \mathrm{FE}$ and $-\Delta \mathrm{G}^{\circ}=n \mathrm{FE}^{\circ}$
Thus from Eq. (i), we get $-n \mathrm{FE}=-n \mathrm{FE}^{\circ}+\mathrm{RT} \ln \mathrm{Q}$
At $25^{\circ} \mathrm{C},$ above equation may be written as $\mathbf{E}=\mathbf{E}^{\mathbf{0}}-\frac{0.0591}{\mathbf{n}} \log \mathbf{Q}$
Where ‘n’ represents number of moles of electrons involved in process.
E, E° are e.m.f. and standard e.m.f. of the cell respectively.
In general , for a redox cell reaction involving the transference of n electrons
$\mathrm{aA}+\mathrm{bB} \longrightarrow \mathrm{cC}+\mathrm{dD},$ the EMF can be calculated as:
$\mathrm{E}_{\mathrm{Cell}}=\mathrm{E}_{\mathrm{Cell}}^{\circ}-\frac{0.0591}{\mathrm{n}} \log \frac{[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}}}{[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}}$
Prediction and feasibility of spontaniety of a cell reaction.
Work done by the cell = nFE;
It is equivalent to decrease in free energy $\Delta \mathrm{G}=-\mathrm{nFE}$
Under standard state $\Delta \mathrm{G}^{0}=-\mathrm{nFE}^{0}$ ..... (i)
(i) From thermodynamics we know, $\Delta$G = negative for spontaneous process. Thus from eq.(i) it is clear that the EMF should be +ve for a cell process to be feasible or spontaneous.
(ii) When $\Delta \mathrm{G}$ = positive, E = negative and the cell process will be non spontaneous.
Standard free energy change of a cell may be calculated by electrode potential data.
Substituting the value of $\mathrm{E}^{0}$ (i.e., standard reduction potentialof cathode- standard reduction potential of anode) in eq. (i) we may get $\Delta \mathrm{G}^{0}$
Let us see whether the cell (Daniell) is feasible or not: i.e. whether Zinc will displace copper or not.
$\mathrm{Zn}|(\mathrm{s})| \mathrm{ZnSO}_{4}(\mathrm{sol}) \| \mathrm{CuSO}_{4}(\mathrm{sol}) | \mathrm{Cu}(\mathrm{s})$
$\mathrm{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{0}=-0.76 \mathrm{volt} ; \mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{0}=+0.34 \mathrm{volt}$
$\mathrm{E}_{\mathrm{cell}}^{0}=\mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{0}-\mathrm{E}_{\mathrm{zn}^{2+} / \mathrm{Zn}}^{0}$
$=0.34-(-0.76)=+1.10 \mathrm{volt}$
Since $\mathrm{E}^{0}=+\mathrm{ve}$, hence the cell will be feasible and zinc will displace copper from its salt solution. In the other words zinc will reduce copper.
8 Thermodynamic treatment of Nernst equation
Determination of equilibrium constant : We know, that
$\mathrm{E}=\mathrm{E}^{0}-\frac{0.0591}{\mathrm{n}} \log \mathrm{Q}$ ..(i)
At equilibrium, the cell potential is zero because cell reactions are balanced, i.e. E = 0
$\therefore$ From Eq. (i), we have
$0=\mathrm{E}^{0}-\frac{0.0591}{\mathrm{n}} \log \mathrm{K}_{\mathrm{eq}} \quad$ or $\quad \mathrm{K}_{\mathrm{eq}}=$ antilog $\left[\frac{n \mathrm{E}^{0}}{0.0591}\right]$
Heat of Reaction inside the cell: Let n Faraday charge flows out of a cell of e.m.f. E, then
$-\Delta \mathrm{G}=n \mathrm{FE}$ ....... (i)
Gibbs Helmholtz equation (from thermodynamics ) may be given as,
$\Delta \mathrm{G}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ ........... (ii)
From Eqs. (i) and (ii), we have
$-\mathrm{nFE}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial(-\mathrm{nFE})}{\partial \mathrm{T}}\right]_{\mathrm{p}}=\Delta \mathrm{H}-\mathrm{nFT}\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$\therefore \Delta \mathrm{H}=-\mathrm{nFE}+\mathrm{nFT}\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
Entropy change inside the cell : We know that G = H - TS or DG = DH - TDS ...(i)
where $\Delta \mathrm{G}$ = Free energy change ; DH = Enthalpy change and DS = entropy change.
According to Gibbs Helmoholtz equation,
$\Delta \mathrm{G}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$\Delta \mathrm{G}=\Delta \mathrm{H}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
From Eqs. (i) and (ii), we have
$-\mathrm{T} \Delta \mathrm{S}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ or $\quad \Delta \mathrm{S}=-\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$-\mathrm{T} \Delta \mathrm{S}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ or $\quad \Delta \mathrm{S}=-\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
where $\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ is called temperature coefficient of cell e.m.f.
8 Different Types of Half-Cells And Their Reduction Potential
(1) Gas-Ion Half Cell:
In such a half cell, an inert collector of electrons, platinum or graphite is in contact with gas and a solution containing a specified ion. One of the most important gas-ion half cell is the hydrogen-gas-hydrogen ion half cell. In this half cell, purified $\mathrm{H}_{2} \mathrm{gas}$ at a constant pressure is passed over a platinum electrode which is in contact with an acid solution.
$\mathrm{H}^{+}(\mathrm{aq})+\mathrm{e}^{-} \rightleftharpoons 1 / 2 \mathrm{H}_{2}$
$\mathrm{E}_{\mathrm{H}^{+} / \mathrm{H}_{2}}=\mathrm{E}^{0}_{\mathrm{H}^{+} / \mathrm{H}_{2}}-\frac{0.0591}{1} \log \frac{\left(\mathrm{pH}_{2}\right)^{1 / 2}}{\left[\mathrm{H}^{+}\right]}$
(2) Metal-Metal Ion Half Cell:
This type of cell consist of a metal M in contact with a solution containing $M^{n+}$ ions.
$\mathrm{M}^{\mathrm{n}+}(\mathrm{aq})+\mathrm{ne}^{-} \rightleftharpoons \mathrm{M}(\mathrm{s})$
$\mathrm{E}_{\mathrm{M}^{\mathrm{n}+} / \mathrm{M}}=\mathrm{E}_{\mathrm{M}^{\mathrm{n}+} / \mathrm{M}}^{0}-\frac{0.0591}{\mathrm{n}} \log \frac{1}{\left[\mathrm{M}^{\mathrm{n}+}\right]}$
(3) Metal-Insoluble Salt - Anion Half Cell:
In this half cell, a metal coated with its insoluble salt is in contact with a solution containing the anion of the insoluble salt. eg. Silver-Silver Chloride Half Cell:
This half cell is represented as CI'AgCl/Ag. The eq
$\mathrm{AgCl}(\mathrm{s})+\mathrm{e}^{-} \rightleftharpoons \mathrm{Ag}(\mathrm{s})+\mathrm{Cl}(\text { aq })$
potential of such cells depends upon the concentration of anions. Such cells can be used as Reference Electrode.
(4) Oxidation-reduction Half Cell:
This type of half cell is made by using an inert metal collector, usually platinum, immersed in a solution which contains two ions of the same element in different states of oxidation. eg. $\mathrm{Fe}^{2+}-\mathrm{Fe}^{3+}$ half cell.
$\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{e}^{-} \rightleftharpoons \mathrm{Fe}^{2+}(\mathrm{aq})$
$\mathrm{E}_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}=\mathrm{E}_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{0}-\frac{0.0591}{1} \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]}$
8 Concentration cell
The cells in which electrical current is produced due to transport of a substance from higherto lower concentration. Concentration gradient may arise either in electrode material or in electrolyte. Thus there are two types of concentration cell .
(i) Electrode concentration cell
(ii) Electrolyte concentration cell
Electrode Gas concentration cell :
$\mathrm{Pt}, \mathrm{H}_{2}\left(\mathrm{P}_{1}\right)\left|\mathrm{H}^{+}(\mathrm{C})\right| \mathrm{H}_{2}\left(\mathrm{P}_{2}\right), \mathrm{Pt}$
Here, hydrogen gas is bubbled at two different partial pressures at electrode dipped in the solution of same electrolyte.
Anode process: $1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{1}\right) \rightarrow \mathrm{H}^{+}(\mathrm{c})+\mathrm{e}^{-}$
Cathode process $\quad \frac{\mathrm{H}^{+}(\mathrm{c})+\mathrm{e}^{-} \rightarrow 1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{2}\right)}{1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{1}\right) \rightarrow 1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{2}\right)}$
$\therefore \quad \mathrm{E}=-\frac{2.303 \mathrm{RT}}{\mathrm{F}} \log \left[\frac{\mathrm{p}_{2}}{\mathrm{p}_{1}}\right]^{1 / 2}$
or $\quad \mathrm{E}=\left[\frac{2.303 \mathrm{RT}}{2 \mathrm{F}}\right] \log \left[\frac{\mathrm{p}_{2}}{\mathrm{p}_{1}}\right], \operatorname{At} 25^{0} \mathrm{C}, \mathrm{E}=\frac{0.059}{2 \mathrm{F}} \log \left[\frac{\mathrm{p}_{1}}{\mathrm{p}_{2}}\right]$
For spontanity of such cell reaction, $\mathrm{p}_{1}>\mathrm{p}_{2}$
Electrolyte concentration cells:
$\mathrm{Zn}(\mathrm{s})\left|\mathrm{ZnSO}_{4}\left(\mathrm{C}_{1}\right) \| \mathrm{ZnSO}_{4}\left(\mathrm{C}_{2}\right)\right| \mathrm{Zn}(\mathrm{s})$
In such cells, concentration gradient arise in electrolyte solutions. Cell process may be givewn a
$\mathrm{zn}(\mathrm{s}) \rightarrow \mathrm{Zn}^{2+}\left(\mathrm{C}_{1}\right)+2 \mathrm{e} \quad$ (Anodic process)
$\frac{\mathrm{Zn}^{2+}\left(\mathrm{C}_{2}\right)+2 \mathrm{e} \rightarrow \mathrm{Zn}(\mathrm{s})}{\mathrm{Zn}^{2+}\left(\mathrm{C}_{2}\right) \rightarrow \mathrm{Zn}^{2+}\left(\mathrm{C}_{1}\right)}$ (Over all process)
$\therefore$ From Nernst equation, we have
$\mathrm{E}=0-\frac{2.303 \mathrm{RT}}{2 \mathrm{F}} \log \left[\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\right]$ OR $\mathrm{E}=\frac{2.303 \mathrm{RT}}{2 \mathrm{F}} \log \left[\frac{\mathrm{C}_{2}}{\mathrm{C}_{1}}\right]$
For spontanity of such cell reaction, $\mathrm{C}_{2}>\mathrm{C}_{1}$
8 CONDUCTANCE
Introduction:
Both metallic and electrolytic conductors obey Ohm's law
i.e. V = IR
where V = Potential difference in volt; I = Current in ampere ; R = resistance in Ohm
We know, resistance is directly proportional to length of conductor and inversely proportional to cross sectional area of the conductor.
$\operatorname{R\propto} \frac{l}{\mathrm{A}} \quad$ or $\mathrm{R}=\rho \frac{l}{\mathrm{A}}$ (= Specific resistance )
Specific resistance is the resistance of a conductor having lengths of 1 cm and corss sectional area of 1cm2.
Unit of R is ohm and unit of specific resistance is ohm cm
Reciprocal of resistance is called as conductance and reciprocal of specific resistance is called as specific conductance.
$\frac{1}{\mathrm{R}}=\frac{1}{\rho} \frac{\mathrm{A}}{l}$ or $\mathrm{C}=\mathrm{K} \frac{\mathrm{A}}{l}$
where C = conductance ohm $^{-1}$; K = specific conductance ohm $^{-1} \mathrm{cm}^{-1}$
Mho and siemens are other units of conductance.
$\mathrm{K}=\frac{l}{\mathrm{A}} \mathrm{C}$
Specific conductance= Cell constant x Conductance
Specific conductance is conductance of 1 $\mathbf{C} \mathbf{M}^{3}$ of an electrolyte solution.
In case of electrolytic solution, the specific conductance is defined as the conductance of a solsution of definite concentration enclosed in a cell having two electrodes sof unit area separated by 1 cm apart.
1. Equivalent Conductance
Equivalent conductance is the conductance of an electrolyte solution containing 1 gm equivalent of electrolyte. It is densoted by $\wedge$ .
$\wedge$ = K x V
$\left(\wedge=\operatorname{ohm}^{-1} \mathrm{cm}^{-1} \mathrm{x} \mathrm{cm}^{3}=\mathrm{ohm}^{-1} \mathrm{cm}^{2}\right)$
Usually concentration of electrolyte solution is expressed as C gm equivalent per litre.
Thus, $\mathrm{V}=\frac{1000}{\mathrm{C}}$
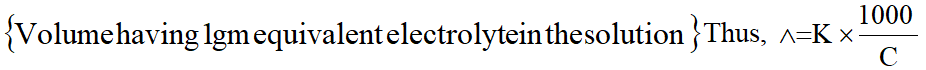2. Molar Conductance
Molar conductance may be defined as conductance of an electrolyte solution having 1 gm mole electrolyte in a litre. It is denoted by $\wedge_{\mathrm{m}}$ .
$\wedge_{\mathrm{m}}=\mathrm{K} \times \mathrm{V}$
Usually concentration of electrolyte solution is expressed as ‘M’ gm mole elecrtrolyte per litre.
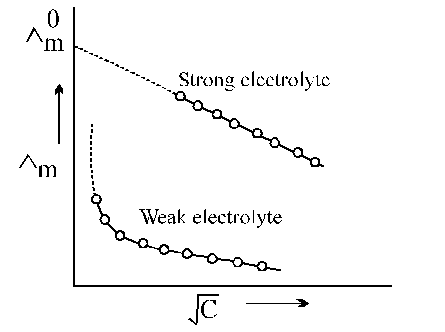The $\dot{\mathrm{U}}_{\mathrm{m}}$ vs $\sqrt{\mathrm{C}}$ plot of strong electrolyte being linear it can be extrapolated to zero concentration. Thus, $\dot{\mathrm{U}}_{\mathrm{m}}$ values of the solution of the test electrolyte are determined at various concentrations the concentrations should be as low as good.
$\dot{\mathrm{U}}_{\mathrm{m}}$ values are then plotted against $\sqrt{\mathrm{C}}$ when a straight line is obtained. This is the extrapolated to zero concentration. The point where the straight line intersects $\dot{\mathrm{U}}_{\mathrm{m}}$ axis is of the strong electrolyte.
However, the plot in the case weak electrolyte being non linear, shooting up suddenly at some low concentration and assuming the shape of a straight line parallel to Ùm axis. Hence extrapolation in this case is not possible. Thus, $\dot{\mathrm{U}}_{0}$of a weak electrolyte cannot be determined experimentally. It can, however, be done with the help of Kohlrausch's law to be discussed later.
8 Kohlrausch's Law of Independent Migration of Ions
Kohlrausch determined $\dot{\mathrm{U}}_{0}$ values of pairs of some strong electrolytes containing same cation say KF and KCl, NaF and NaCl etc., and found that the difference in $\dot{\mathrm{U}}_{0}$ values in each case remains the same:
$\wedge_{\mathrm{m}}^{0}(\mathrm{KCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{KF})=\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaF})$
He also detemined $\dot{\mathrm{U}}_{0}$ values of pairs of strong electrolytes containing same anion say KF and NaF, KCl and NaCl etc.and found that the difference in Ù0 values in each case remains the same.
$\wedge_{\mathrm{m}}^{0}(\mathrm{KF})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaF})=\wedge_{\mathrm{m}}^{0}(\mathrm{KCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})$
At infinite dilution when dissociation is complete, every ion makes some definite contribution towards molar conductance of the electrolyte irrespective of the nature of the other ion which with it is associated and that the molar conductance at infinite dilution for any electrolyte is given by the sum of the contribution of the two ions. Thus,
$\wedge_{\mathrm{m}}^{0}=\lambda_{+}^{0}+\lambda_{-}^{0}$
Where $\lambda_{+}^{0}$ is the contribution of the cation and $\lambda_{-}^{0}$ is the contribution of the anion towards the molar conductance at infinite dilution. These contributions are called molar ionic conductances at infinite dilution. Thus, $\lambda_{+}^{0}$ is the molar ionic conductance of cation and
$\lambda_{-}^{0}$ is the molar ionic conductnace of anion, at infinite dilution. The above equation is, however, correct only for binary electrolyte like NaCl, $\mathrm{MgSO}_{4}$ etc.
8 Application of Kohlrausch's law :
(1) Determination of $\wedge_{\mathrm{m}}^{0}$ of a weak electrolyte:
In order to calculate $\wedge_{\mathrm{m}}^{0}$ of a weak electrolyte say CH3COOH, we determine experimentally $\wedge_{\mathrm{m}}^{0}$ values of
the following three strong electrolytes:
(a) A strong electrolyte containing same cation as in the test electrolyte, say HCl
(b) A strong electrolyte containing same anion as in the test electrolyte, say $\mathrm{CH}_{3} \mathrm{COONa}$
(c) A strong electrolyte containing same anion of (a) and cation of (b) i.e. NaCl.
$\wedge_{\mathrm{m}}^{0}$ of $\mathrm{CH}_{3} \mathrm{COOH}$ is then given as:
$\wedge_{\mathrm{m}}^{0}\left(\mathrm{CH}_{3} \mathrm{COOH}\right)=\wedge_{\mathrm{m}}^{0}(\mathrm{HCl})+\wedge_{\mathrm{m}}^{0}\left(\mathrm{CH}_{3} \mathrm{COONa}\right)-\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})$
Proof:
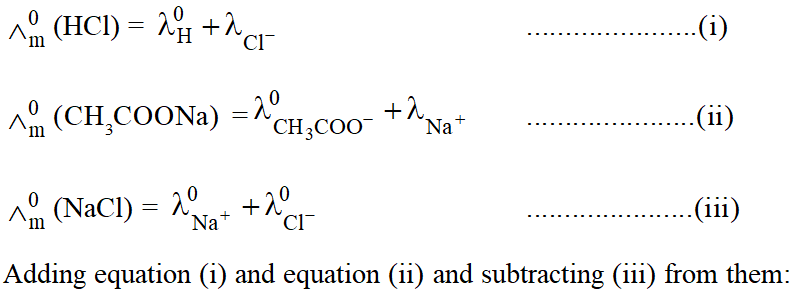$\wedge_{\mathrm{m}}^{0}(\mathrm{HCl})+\wedge_{\left(\mathrm{CH}_{3} \mathrm{COONa}\right)}^{0}-\wedge_{(\mathrm{NaCl})}^{0}=\lambda_{\left(\mathrm{H}^{+}\right)}^{0}+\lambda_{\left(\mathrm{CH}_{3} \mathrm{COO}^{0}\right)}^{0}=\wedge_{0\left(\mathrm{CH}_{3} \mathrm{COOH}\right)}$
(2) Determination of degree of dissociation (a) :
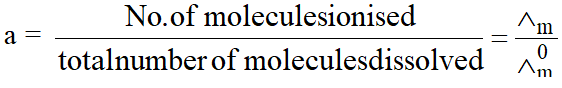(3) Determination of solubility of sparingly soluble salt
The specific conductivity of a saturated solution of the test electrolyte (sparingly soluble) made in conductivity water is determined by the method as described above. From this the specific conductivity of conductivity water is deducted. The molar conductance of the saturated solution is taken to be equal to $\wedge_{\mathrm{m}}^{0}$ as the saturated solution of a sparingly soluble salt is extremely dilute.
$\wedge_{\mathrm{m}}^{0}=\frac{1000 \mathrm{\kappa}}{\mathrm{C}}$
where C is the molarity of solution and hence the solubility.
Electrolysis of Molten sodium chloride
$\mathrm{NaCl}(\mathrm{molten}) \longrightarrow \mathrm{Na}^{+}+\mathrm{Cl}^{-}$
There are two types of electrodes used in the electroytic cell, namely attackable and non - attackable. The attackable elecrodes participitate in the electrode reaction. They are made up of reactive metals like Zn, Cu, Ag etc. In such electrodes, atom of the metal gets oxidised into the corresponding cation, which is passed into the solution. Thus, such anodes get dissolved and their mass decreases. On the other hand, non-attackable electrodes do not participiate in the electrode reaction as they made up of unreactive elements like Pt, graphite etc. Such electrodes do not dissolve and their mass remain same.
Faraday’s laws of electrolysis:
(i) First law of electrolysis :
Amount of substance deposited or liberated at an electrode is directly proportional to amount of charge passed (utilized) through the solution.
$\mathrm{w} \propto \mathrm{Q}$
W = weight liberated, Q = charge in coulomb
w = ZQ
Z = electrochemical equivalent
when Q = 1 coulomb, then w = Z
Thus, weight deposited by 1 coulomb charge is called electrochemical equivalent.
Let 1 ampere current is passed till ‘t’ seconds .
Then, Q = It w = ZIt
1 Faraday = 96500 coulomb = Charge of one mole electrons
One faraday is the charge required to liberate or deposit one gm equivalent of a substance at corresponding electrode.
Let ‘E’ is equivalent weight then ‘E’ gm will be liberated by 96500 coulomb.
$\therefore 1$ Coulomb will liberate $\frac{\mathrm{E}}{96500} \mathrm{gm} ;$ By definition, $Z=\frac{\mathrm{E}}{96500}$
$\therefore W=\frac{I t E}{96500}$
When a gas is evolved at an electrode, then above formula changes as,
$\mathrm{V}=\frac{\mathrm{ItV}_{\mathrm{e}}}{96500}$
where V = volume of liberated gas, $\mathrm{V}_{\mathrm{e}}$ = equivalent volume of gas.
Equivalent volume may be defined as:
The volume of gas liberated by 96500 coulomb at STP.
(ii) Second law of electrolysis :
When same amount of charge is passed through different electrolyte solutions connected in series then weight of substances deposited or dissolved at anode or cathode are in ratio of their equivalent weights. i.e.
$\mathrm{w}_{1} / \mathrm{w}_{2}=\mathrm{E}_{1} / \mathrm{E}_{2}$
QUALITATIVE ASPECTS OF ELECTROLYSIS
In the electrolysis process we have discussed above, we have taken molten salt as electrolyte, which contains only one cation and anion. Now, if the electrolyte taken contains more than one cation and anion (for example, aqueous solution of the ionic electrolyte), then the cation and anion that will get discharged depends on the ability of cation to get reduced and the ability of anion to get oxidised.
The ability of an ion to get oxidised or reduced depends upon the size, mass, positive charge, negative charge etc. Thus, it is not possible to predict qualitatively that which ion would be discharged first, a one factor might enhance the ability to discharge while the other factor may hamper it. This can only be predicted on the basis of quantitative value assigned based on the cumulative effect of all the factors reponsible for an ion's ability to discharge. The value is referred as standard potential, which is determined by keeping the concentration of ion as 1 M, pressure of gas at 1 atm, and the measurement done at $25^{\circ} \mathrm{C}$. For a cation, the standard reduction potential (SRP) values are compared. The cation having higher standard reduction potential value is discharged in preference to cation with lower SRP value provided the ions are at 1 M concentration. For an anion, the standard oxidation potential (SOP) values are compared and anion having higher SOP is preferentially discharged, if the concentration is 1 M for each of the ion. The SRP values at $25^{\circ} \mathrm{C}$for some of the reduction half reactions are given in the table below.
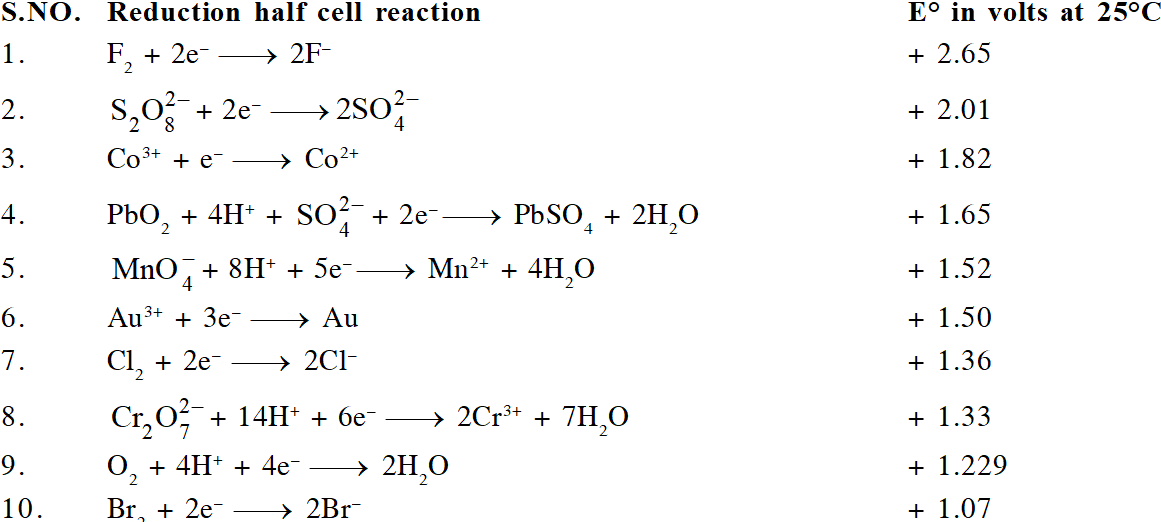
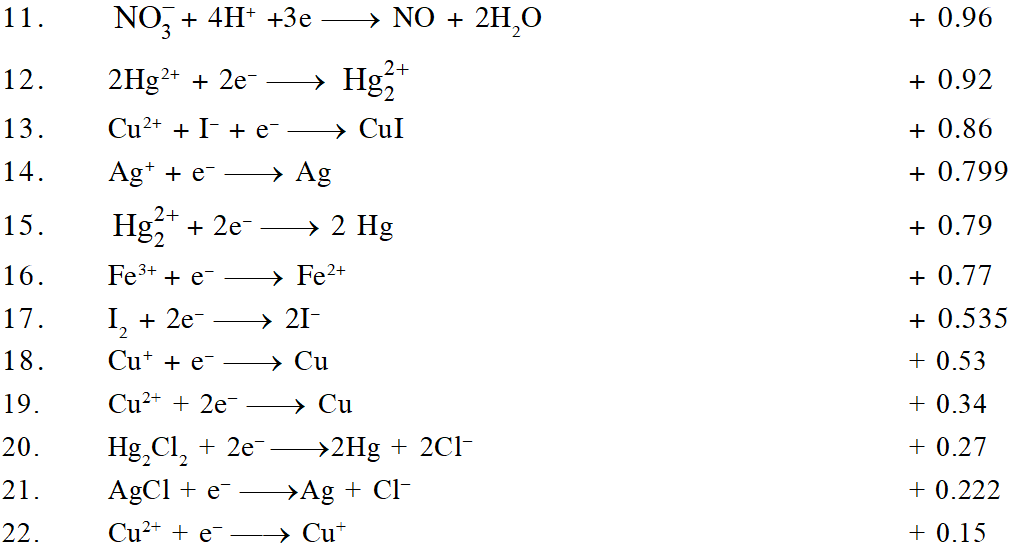
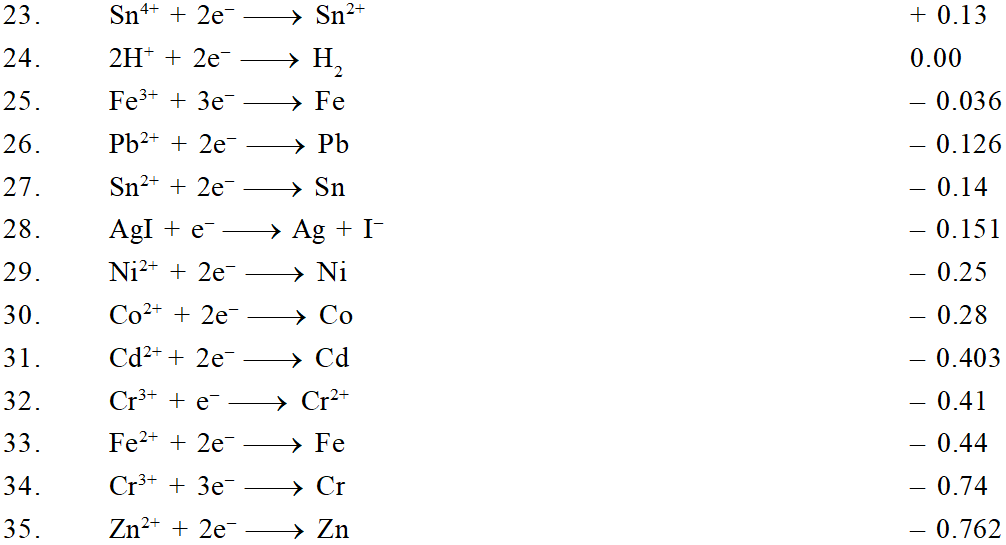
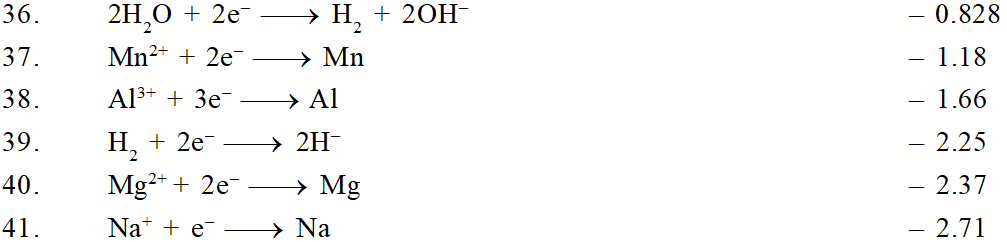
When solution of an electroyte contains more than one type of cations and anions at concentrations different than 1 M, the discharge of an ion does not depend solely on standard potentials but also depends on the concentration of ion in the solution. This value is refered as potential, called as reduction potential for cation and oxidation potential for anion. The relation between reduction potential and standard reduction potential is given by Nernst equation, as
$\mathrm{E}_{\mathrm{RP}}=\mathrm{E}_{\mathrm{RP}}^{\circ}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln \frac{[\text { concentration of product }]}{[\text { concentration of reac tan } \mathrm{t}]}$
where $E_{R P}$ = Reduction potential of cation and $\mathrm{E}^{\mathrm{O}} \mathrm{RP}$= Standard reduction potential of cation.
Thus, it is possible that a cation (A+) with lower standard reduction potential getting discharged in preference to cation $\left(\mathrm{B}^{+}\right)$ having higher standard reduction potential because their concentration might be such that the reduction potential of $\mathrm{A}^{+}$ is higher than that of $\mathrm{B}^{+}$.
When two metal ions in the solution have identical values of their reduction potentials, the simultaneous deposition of both the metals will occur in the form of an alloy.
Galvanic Cell
This cell converts chemical energy into electrical energy.
Galvanic cell is made up of two half cells i.e., anodic and cathodic. The cell reaction is of redox kind. Oxidation takes place at anode and reduction at cathode. It is also known as voltaic cell. It may be represented as shown in Fig. Zinc rod immersed in $\mathrm{ZnSO}_{4}$ behaves as anode and copper rod immersed in $\mathrm{CuSO}_{4}$ behaves as cathode.
Oxidation takes place at anode:
$\mathrm{Zn}^{3 / 4} \rightarrow \mathrm{Zn}^{2+}+2 \mathrm{e}^{-}$ (loss of electron : oxidation)
Reduction takes place at cathode:
$\mathrm{Cu}^{2+}+2 \mathrm{e}^{-} \longrightarrow \mathrm{Cu}(\text { gain of electron } ; \text { reduction })$
Over all process:
$\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+} \longrightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}$
In galvanic cell like Daniell cell; electrons flow from anode (zinc rod) to the cathode (copper rod) through external circuit; zinc dissolves as $\mathrm{Zn}^{2+} ; \mathrm{Cu}^{2+}$ion in the cathode cell picks up two electron and become deposited at cathode.
Salt Bridge
Two electrolyte solutions in galvanic cells are seperated using salt bridge as represented in the Fig. salt bridge is a device to minimize or eliminate the liquid junction potential. Saturated solution of salt like KCI, $\mathrm{KNO}_{3}$, $\mathrm{NH}_{4} \mathrm{Cl}$ and $\mathrm{NH}_{4} \mathrm{NO}_{3}$ etc. in agar-agar gel is used in salt bridge. Salt bridge contains high concentration of ions viz. $\mathrm{K}^{+}$ and $\mathrm{NO}_{3}^{-}$at the junction with electrolyte solution. Thus, salt bridge carries whole of the current across the boundary ; more over the $\mathrm{K}^{+}$ and $\mathrm{NO}_{3}^{-}$ ions have same speed. Hence, salt bridge with uniform and same mobility of cations and anions minimize the liquid junction potential & completes the electrical circuit & permits the ions to migrate.
Representation of a cell (IUPAC conventions ): Let us illustrate the convention taking the example of Daniel cell.
(i) Anodic half cell is written on left and cathodic half cell on right hand sid
$\mathrm{Zn}(\mathrm{s})\left|\mathrm{ZnSO}_{4}(\mathrm{sol}) \| \mathrm{CuSO}_{4}(\mathrm{sol})\right| \mathrm{Cu}(\mathrm{s})$
(ii) Two half cells are separated by double vertical lines: Double vertical lines indicate salt bridge or any type of porous partition.
(iii) EMF (electromotive force) may be written on the right hand side of the cell.
(iv) Single vertical lines indicate the phase separation between electrode and electrolyte solution.
$\mathrm{Zn}\left|\mathrm{Zn}^{2+} \| \mathrm{Cu}^{2+}\right| \mathrm{Cu}$
Concept of Electromotive force (EMF) of a Cell
Electron flows from anode to cathode in external circuit due to a pushing effect called or electromotic force (e.m.f.). E.m.f. is some times called as cell potential. Unit of e.m.f. of cell is volt.
EMF of cell may be calculated as :
$E_{\operatorname{cell}}$ reduction potential of cathode - Reduction potential of anode
Similarly, standard e.m.f. of the cell $\left(\mathrm{E}^{\circ}\right)$ may be calculated as
$\mathrm{E}_{\text {cell }}^{\circ}$ = Standard reduction potential of cathode - Standard reduction potential of anode
Sign Convention of EMF
EMF of cell should be positive other wise it will not be feasible in the given direction .
$\begin{array}{ll}{\mathrm{Zn}\left|\mathrm{ZnSO}_{4} \| \mathrm{CuSO}_{4}\right| \mathrm{Cu}} & {\mathrm{E}=+1.10 \text { volt } \quad \text { (Feasible) }} \\ {\mathrm{Cu}\left|\mathrm{CuSO}_{4} \| \mathrm{ZnSO}_{4}\right| \mathrm{Zn}} & {\mathrm{E}=-1.10 \text { volt } \quad \text { (Not Feasible) }}\end{array}$
Nernst Equation
Walter Nernst derived a relation between cell potential and concentration or Reaction quotient.
$\Delta \mathrm{G}=\Delta \mathrm{G}^{\circ}+\mathrm{R} \mathrm{T} \ln \mathrm{Q}$ $\ldots .(1)$
where $\Delta \mathrm{G}$ and $\Delta \mathrm{G}^{\circ}$are free energy and standard free energy change; ‘Q’ is reaction quotient.
Let n, Faraday charge is taken out from a cell of e.m.f. (E) then electrical work done by the cell may be calculated as,
Work done = Charge x Potential = nFE
From thermodynamics we know that decrease in Gibbs free energy of a system is a measure of reversible or maximum obtainable work by the system if there is no work due to volume expans
$\therefore-\Delta \mathrm{G}=n \mathrm{FE}$ and $-\Delta \mathrm{G}^{\circ}=n \mathrm{FE}^{\circ}$
Thus from Eq. (i), we get $-n \mathrm{FE}=-n \mathrm{FE}^{\circ}+\mathrm{RT} \ln \mathrm{Q}$
At $25^{\circ} \mathrm{C},$ above equation may be written as $\mathbf{E}=\mathbf{E}^{\mathbf{0}}-\frac{0.0591}{\mathbf{n}} \log \mathbf{Q}$
Where ‘n’ represents number of moles of electrons involved in process.
E, E° are e.m.f. and standard e.m.f. of the cell respectively.
In general , for a redox cell reaction involving the transference of n electrons
$\mathrm{aA}+\mathrm{bB} \longrightarrow \mathrm{cC}+\mathrm{dD},$ the EMF can be calculated as:
$\mathrm{E}_{\mathrm{Cell}}=\mathrm{E}_{\mathrm{Cell}}^{\circ}-\frac{0.0591}{\mathrm{n}} \log \frac{[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}}}{[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}}$
Prediction and feasibility of spontaniety of a cell reaction.
Work done by the cell = nFE;
It is equivalent to decrease in free energy $\Delta \mathrm{G}=-\mathrm{nFE}$
Under standard state $\Delta \mathrm{G}^{0}=-\mathrm{nFE}^{0}$ ..... (i)
(i) From thermodynamics we know, $\Delta$G = negative for spontaneous process. Thus from eq.(i) it is clear that the EMF should be +ve for a cell process to be feasible or spontaneous.
(ii) When $\Delta \mathrm{G}$ = positive, E = negative and the cell process will be non spontaneous.
Standard free energy change of a cell may be calculated by electrode potential data.
Substituting the value of $\mathrm{E}^{0}$ (i.e., standard reduction potentialof cathode- standard reduction potential of anode) in eq. (i) we may get $\Delta \mathrm{G}^{0}$
Let us see whether the cell (Daniell) is feasible or not: i.e. whether Zinc will displace copper or not.
$\mathrm{Zn}|(\mathrm{s})| \mathrm{ZnSO}_{4}(\mathrm{sol}) \| \mathrm{CuSO}_{4}(\mathrm{sol}) | \mathrm{Cu}(\mathrm{s})$
$\mathrm{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{0}=-0.76 \mathrm{volt} ; \mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{0}=+0.34 \mathrm{volt}$
$\mathrm{E}_{\mathrm{cell}}^{0}=\mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{0}-\mathrm{E}_{\mathrm{zn}^{2+} / \mathrm{Zn}}^{0}$
$=0.34-(-0.76)=+1.10 \mathrm{volt}$
Since $\mathrm{E}^{0}=+\mathrm{ve}$, hence the cell will be feasible and zinc will displace copper from its salt solution. In the other words zinc will reduce copper.
8 Thermodynamic treatment of Nernst equation
Determination of equilibrium constant : We know, that
$\mathrm{E}=\mathrm{E}^{0}-\frac{0.0591}{\mathrm{n}} \log \mathrm{Q}$ ..(i)
At equilibrium, the cell potential is zero because cell reactions are balanced, i.e. E = 0
$\therefore$ From Eq. (i), we have
$0=\mathrm{E}^{0}-\frac{0.0591}{\mathrm{n}} \log \mathrm{K}_{\mathrm{eq}} \quad$ or $\quad \mathrm{K}_{\mathrm{eq}}=$ antilog $\left[\frac{n \mathrm{E}^{0}}{0.0591}\right]$
Heat of Reaction inside the cell: Let n Faraday charge flows out of a cell of e.m.f. E, then
$-\Delta \mathrm{G}=n \mathrm{FE}$ ....... (i)
Gibbs Helmholtz equation (from thermodynamics ) may be given as,
$\Delta \mathrm{G}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ ........... (ii)
From Eqs. (i) and (ii), we have
$-\mathrm{nFE}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial(-\mathrm{nFE})}{\partial \mathrm{T}}\right]_{\mathrm{p}}=\Delta \mathrm{H}-\mathrm{nFT}\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$\therefore \Delta \mathrm{H}=-\mathrm{nFE}+\mathrm{nFT}\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
Entropy change inside the cell : We know that G = H - TS or DG = DH - TDS ...(i)
where $\Delta \mathrm{G}$ = Free energy change ; DH = Enthalpy change and DS = entropy change.
According to Gibbs Helmoholtz equation,
$\Delta \mathrm{G}=\Delta \mathrm{H}+\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$\Delta \mathrm{G}=\Delta \mathrm{H}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
From Eqs. (i) and (ii), we have
$-\mathrm{T} \Delta \mathrm{S}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ or $\quad \Delta \mathrm{S}=-\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
$-\mathrm{T} \Delta \mathrm{S}=\mathrm{T}\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ or $\quad \Delta \mathrm{S}=-\left[\frac{\partial \Delta \mathrm{G}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$
where $\left[\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right]_{\mathrm{p}}$ is called temperature coefficient of cell e.m.f.
8 Different Types of Half-Cells And Their Reduction Potential
(1) Gas-Ion Half Cell:
In such a half cell, an inert collector of electrons, platinum or graphite is in contact with gas and a solution containing a specified ion. One of the most important gas-ion half cell is the hydrogen-gas-hydrogen ion half cell. In this half cell, purified $\mathrm{H}_{2} \mathrm{gas}$ at a constant pressure is passed over a platinum electrode which is in contact with an acid solution.
$\mathrm{H}^{+}(\mathrm{aq})+\mathrm{e}^{-} \rightleftharpoons 1 / 2 \mathrm{H}_{2}$
$\mathrm{E}_{\mathrm{H}^{+} / \mathrm{H}_{2}}=\mathrm{E}^{0}_{\mathrm{H}^{+} / \mathrm{H}_{2}}-\frac{0.0591}{1} \log \frac{\left(\mathrm{pH}_{2}\right)^{1 / 2}}{\left[\mathrm{H}^{+}\right]}$
(2) Metal-Metal Ion Half Cell:
This type of cell consist of a metal M in contact with a solution containing $M^{n+}$ ions.
$\mathrm{M}^{\mathrm{n}+}(\mathrm{aq})+\mathrm{ne}^{-} \rightleftharpoons \mathrm{M}(\mathrm{s})$
$\mathrm{E}_{\mathrm{M}^{\mathrm{n}+} / \mathrm{M}}=\mathrm{E}_{\mathrm{M}^{\mathrm{n}+} / \mathrm{M}}^{0}-\frac{0.0591}{\mathrm{n}} \log \frac{1}{\left[\mathrm{M}^{\mathrm{n}+}\right]}$
(3) Metal-Insoluble Salt - Anion Half Cell:
In this half cell, a metal coated with its insoluble salt is in contact with a solution containing the anion of the insoluble salt. eg. Silver-Silver Chloride Half Cell:
This half cell is represented as CI'AgCl/Ag. The eq
$\mathrm{AgCl}(\mathrm{s})+\mathrm{e}^{-} \rightleftharpoons \mathrm{Ag}(\mathrm{s})+\mathrm{Cl}(\text { aq })$
potential of such cells depends upon the concentration of anions. Such cells can be used as Reference Electrode.
(4) Oxidation-reduction Half Cell:
This type of half cell is made by using an inert metal collector, usually platinum, immersed in a solution which contains two ions of the same element in different states of oxidation. eg. $\mathrm{Fe}^{2+}-\mathrm{Fe}^{3+}$ half cell.
$\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{e}^{-} \rightleftharpoons \mathrm{Fe}^{2+}(\mathrm{aq})$
$\mathrm{E}_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}=\mathrm{E}_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{0}-\frac{0.0591}{1} \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]}$
8 Concentration cell
The cells in which electrical current is produced due to transport of a substance from higherto lower concentration. Concentration gradient may arise either in electrode material or in electrolyte. Thus there are two types of concentration cell .
(i) Electrode concentration cell
(ii) Electrolyte concentration cell
Electrode Gas concentration cell :
$\mathrm{Pt}, \mathrm{H}_{2}\left(\mathrm{P}_{1}\right)\left|\mathrm{H}^{+}(\mathrm{C})\right| \mathrm{H}_{2}\left(\mathrm{P}_{2}\right), \mathrm{Pt}$
Here, hydrogen gas is bubbled at two different partial pressures at electrode dipped in the solution of same electrolyte.
Anode process: $1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{1}\right) \rightarrow \mathrm{H}^{+}(\mathrm{c})+\mathrm{e}^{-}$
Cathode process $\quad \frac{\mathrm{H}^{+}(\mathrm{c})+\mathrm{e}^{-} \rightarrow 1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{2}\right)}{1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{1}\right) \rightarrow 1 / 2 \mathrm{H}_{2}\left(\mathrm{p}_{2}\right)}$
$\therefore \quad \mathrm{E}=-\frac{2.303 \mathrm{RT}}{\mathrm{F}} \log \left[\frac{\mathrm{p}_{2}}{\mathrm{p}_{1}}\right]^{1 / 2}$
or $\quad \mathrm{E}=\left[\frac{2.303 \mathrm{RT}}{2 \mathrm{F}}\right] \log \left[\frac{\mathrm{p}_{2}}{\mathrm{p}_{1}}\right], \operatorname{At} 25^{0} \mathrm{C}, \mathrm{E}=\frac{0.059}{2 \mathrm{F}} \log \left[\frac{\mathrm{p}_{1}}{\mathrm{p}_{2}}\right]$
For spontanity of such cell reaction, $\mathrm{p}_{1}>\mathrm{p}_{2}$
Electrolyte concentration cells:
$\mathrm{Zn}(\mathrm{s})\left|\mathrm{ZnSO}_{4}\left(\mathrm{C}_{1}\right) \| \mathrm{ZnSO}_{4}\left(\mathrm{C}_{2}\right)\right| \mathrm{Zn}(\mathrm{s})$
In such cells, concentration gradient arise in electrolyte solutions. Cell process may be givewn a
$\mathrm{zn}(\mathrm{s}) \rightarrow \mathrm{Zn}^{2+}\left(\mathrm{C}_{1}\right)+2 \mathrm{e} \quad$ (Anodic process)
$\frac{\mathrm{Zn}^{2+}\left(\mathrm{C}_{2}\right)+2 \mathrm{e} \rightarrow \mathrm{Zn}(\mathrm{s})}{\mathrm{Zn}^{2+}\left(\mathrm{C}_{2}\right) \rightarrow \mathrm{Zn}^{2+}\left(\mathrm{C}_{1}\right)}$ (Over all process)
$\therefore$ From Nernst equation, we have
$\mathrm{E}=0-\frac{2.303 \mathrm{RT}}{2 \mathrm{F}} \log \left[\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\right]$ OR $\mathrm{E}=\frac{2.303 \mathrm{RT}}{2 \mathrm{F}} \log \left[\frac{\mathrm{C}_{2}}{\mathrm{C}_{1}}\right]$
For spontanity of such cell reaction, $\mathrm{C}_{2}>\mathrm{C}_{1}$
8 CONDUCTANCE
Introduction:
Both metallic and electrolytic conductors obey Ohm's law
i.e. V = IR
where V = Potential difference in volt; I = Current in ampere ; R = resistance in Ohm
We know, resistance is directly proportional to length of conductor and inversely proportional to cross sectional area of the conductor.
$\operatorname{R\propto} \frac{l}{\mathrm{A}} \quad$ or $\mathrm{R}=\rho \frac{l}{\mathrm{A}}$ (= Specific resistance )
Specific resistance is the resistance of a conductor having lengths of 1 cm and corss sectional area of 1cm2.
Unit of R is ohm and unit of specific resistance is ohm cm
Reciprocal of resistance is called as conductance and reciprocal of specific resistance is called as specific conductance.
$\frac{1}{\mathrm{R}}=\frac{1}{\rho} \frac{\mathrm{A}}{l}$ or $\mathrm{C}=\mathrm{K} \frac{\mathrm{A}}{l}$
where C = conductance ohm $^{-1}$; K = specific conductance ohm $^{-1} \mathrm{cm}^{-1}$
Mho and siemens are other units of conductance.
$\mathrm{K}=\frac{l}{\mathrm{A}} \mathrm{C}$
Specific conductance= Cell constant x Conductance
Specific conductance is conductance of 1 $\mathbf{C} \mathbf{M}^{3}$ of an electrolyte solution.
In case of electrolytic solution, the specific conductance is defined as the conductance of a solsution of definite concentration enclosed in a cell having two electrodes sof unit area separated by 1 cm apart.
1. Equivalent Conductance
Equivalent conductance is the conductance of an electrolyte solution containing 1 gm equivalent of electrolyte. It is densoted by $\wedge$ .
$\wedge$ = K x V
$\left(\wedge=\operatorname{ohm}^{-1} \mathrm{cm}^{-1} \mathrm{x} \mathrm{cm}^{3}=\mathrm{ohm}^{-1} \mathrm{cm}^{2}\right)$
Usually concentration of electrolyte solution is expressed as C gm equivalent per litre.
Thus, $\mathrm{V}=\frac{1000}{\mathrm{C}}$
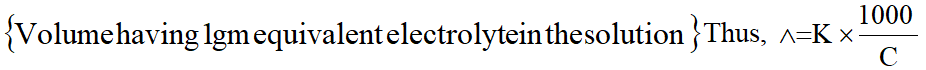2. Molar Conductance
Molar conductance may be defined as conductance of an electrolyte solution having 1 gm mole electrolyte in a litre. It is denoted by $\wedge_{\mathrm{m}}$ .
$\wedge_{\mathrm{m}}=\mathrm{K} \times \mathrm{V}$
Usually concentration of electrolyte solution is expressed as ‘M’ gm mole elecrtrolyte per litre.
The $\dot{\mathrm{U}}_{\mathrm{m}}$ vs $\sqrt{\mathrm{C}}$ plot of strong electrolyte being linear it can be extrapolated to zero concentration. Thus, $\dot{\mathrm{U}}_{\mathrm{m}}$ values of the solution of the test electrolyte are determined at various concentrations the concentrations should be as low as good.
$\dot{\mathrm{U}}_{\mathrm{m}}$ values are then plotted against $\sqrt{\mathrm{C}}$ when a straight line is obtained. This is the extrapolated to zero concentration. The point where the straight line intersects $\dot{\mathrm{U}}_{\mathrm{m}}$ axis is of the strong electrolyte.
However, the plot in the case weak electrolyte being non linear, shooting up suddenly at some low concentration and assuming the shape of a straight line parallel to Ùm axis. Hence extrapolation in this case is not possible. Thus, $\dot{\mathrm{U}}_{0}$of a weak electrolyte cannot be determined experimentally. It can, however, be done with the help of Kohlrausch's law to be discussed later.
8 Kohlrausch's Law of Independent Migration of Ions
Kohlrausch determined $\dot{\mathrm{U}}_{0}$ values of pairs of some strong electrolytes containing same cation say KF and KCl, NaF and NaCl etc., and found that the difference in $\dot{\mathrm{U}}_{0}$ values in each case remains the same:
$\wedge_{\mathrm{m}}^{0}(\mathrm{KCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{KF})=\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaF})$
He also detemined $\dot{\mathrm{U}}_{0}$ values of pairs of strong electrolytes containing same anion say KF and NaF, KCl and NaCl etc.and found that the difference in Ù0 values in each case remains the same.
$\wedge_{\mathrm{m}}^{0}(\mathrm{KF})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaF})=\wedge_{\mathrm{m}}^{0}(\mathrm{KCl})-\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})$
At infinite dilution when dissociation is complete, every ion makes some definite contribution towards molar conductance of the electrolyte irrespective of the nature of the other ion which with it is associated and that the molar conductance at infinite dilution for any electrolyte is given by the sum of the contribution of the two ions. Thus,
$\wedge_{\mathrm{m}}^{0}=\lambda_{+}^{0}+\lambda_{-}^{0}$
Where $\lambda_{+}^{0}$ is the contribution of the cation and $\lambda_{-}^{0}$ is the contribution of the anion towards the molar conductance at infinite dilution. These contributions are called molar ionic conductances at infinite dilution. Thus, $\lambda_{+}^{0}$ is the molar ionic conductance of cation and
$\lambda_{-}^{0}$ is the molar ionic conductnace of anion, at infinite dilution. The above equation is, however, correct only for binary electrolyte like NaCl, $\mathrm{MgSO}_{4}$ etc.
8 Application of Kohlrausch's law :
(1) Determination of $\wedge_{\mathrm{m}}^{0}$ of a weak electrolyte:
In order to calculate $\wedge_{\mathrm{m}}^{0}$ of a weak electrolyte say CH3COOH, we determine experimentally $\wedge_{\mathrm{m}}^{0}$ values of
the following three strong electrolytes:
(a) A strong electrolyte containing same cation as in the test electrolyte, say HCl
(b) A strong electrolyte containing same anion as in the test electrolyte, say $\mathrm{CH}_{3} \mathrm{COONa}$
(c) A strong electrolyte containing same anion of (a) and cation of (b) i.e. NaCl.
$\wedge_{\mathrm{m}}^{0}$ of $\mathrm{CH}_{3} \mathrm{COOH}$ is then given as:
$\wedge_{\mathrm{m}}^{0}\left(\mathrm{CH}_{3} \mathrm{COOH}\right)=\wedge_{\mathrm{m}}^{0}(\mathrm{HCl})+\wedge_{\mathrm{m}}^{0}\left(\mathrm{CH}_{3} \mathrm{COONa}\right)-\wedge_{\mathrm{m}}^{0}(\mathrm{NaCl})$
Proof:
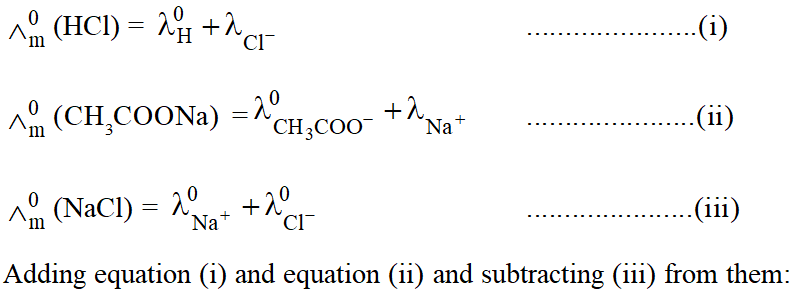$\wedge_{\mathrm{m}}^{0}(\mathrm{HCl})+\wedge_{\left(\mathrm{CH}_{3} \mathrm{COONa}\right)}^{0}-\wedge_{(\mathrm{NaCl})}^{0}=\lambda_{\left(\mathrm{H}^{+}\right)}^{0}+\lambda_{\left(\mathrm{CH}_{3} \mathrm{COO}^{0}\right)}^{0}=\wedge_{0\left(\mathrm{CH}_{3} \mathrm{COOH}\right)}$
(2) Determination of degree of dissociation (a) :
(3) Determination of solubility of sparingly soluble salt
The specific conductivity of a saturated solution of the test electrolyte (sparingly soluble) made in conductivity water is determined by the method as described above. From this the specific conductivity of conductivity water is deducted. The molar conductance of the saturated solution is taken to be equal to $\wedge_{\mathrm{m}}^{0}$ as the saturated solution of a sparingly soluble salt is extremely dilute.
$\wedge_{\mathrm{m}}^{0}=\frac{1000 \mathrm{\kappa}}{\mathrm{C}}$
where C is the molarity of solution and hence the solubility.