JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. An inductor of inductance L = 400 mH and resistors of resistances $\mathrm{R}_{1}=2 \Omega$ and $\mathrm{R}_{2}$= $2 \Omega$ are connected to a battery of emf 12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t = 0. The potential drop across L as a function of time is:-
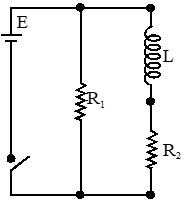 (1) $6\left(1-\mathrm{e}^{-\mathrm{t} / 0.2}\right) \mathrm{V}$
(2) $12 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
(3) $6 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
( 4)$\frac{12}{\mathrm{t}} e^{-3 \mathrm{t}} \mathrm{V}$
[AIEEE - 2009]
(1) $6\left(1-\mathrm{e}^{-\mathrm{t} / 0.2}\right) \mathrm{V}$
(2) $12 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
(3) $6 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
( 4)$\frac{12}{\mathrm{t}} e^{-3 \mathrm{t}} \mathrm{V}$
[AIEEE - 2009]
 (1) $6\left(1-\mathrm{e}^{-\mathrm{t} / 0.2}\right) \mathrm{V}$
(2) $12 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
(3) $6 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
( 4)$\frac{12}{\mathrm{t}} e^{-3 \mathrm{t}} \mathrm{V}$
[AIEEE - 2009]
(1) $6\left(1-\mathrm{e}^{-\mathrm{t} / 0.2}\right) \mathrm{V}$
(2) $12 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
(3) $6 \mathrm{e}^{-5 \mathrm{t}} \mathrm{V}$
( 4)$\frac{12}{\mathrm{t}} e^{-3 \mathrm{t}} \mathrm{V}$
[AIEEE - 2009]
Ans. (2)
$I=I_{0} e^{-\frac{R T}{L}}$
Q. In the circuit show below, the key K is closed at t = 0. The current through the battery is :
(1) $\frac{V\left(R_{1}+R_{2}\right)}{R_{1} R_{2}}$ at $t=0$ and $\frac{V}{R_{2}}$ at $t=\infty$
(2) $\frac{\mathrm{VR}_{1} \mathrm{R}_{2}}{\sqrt{\mathrm{R}_{1}^{2}+\mathrm{R}_{2}^{2}}}$ at $\mathrm{t}=0$ and $\frac{\mathrm{V}}{\mathrm{R}_{2}}$ at $\mathrm{t}=\infty$
(3) $\frac{\mathrm{V}}{\mathrm{R}_{2}}$ at $\mathrm{t}=0$ and $\frac{\mathrm{V}\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}{\mathrm{R}_{1} \mathrm{R}_{2}}$ at $\mathrm{t}=\infty$
(4) $\frac{\mathrm{V}}{\mathrm{R}_{2}}$ at $\mathrm{t}=0$ and $\frac{\mathrm{VR}_{1} \mathrm{R}_{2}}{\sqrt{\mathrm{R}_{1}^{2}+\mathrm{R}_{2}^{2}}}$ at $\mathrm{t}=\infty$
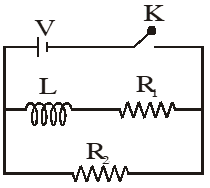 [AIEEE - 2010]
[AIEEE - 2010]
 [AIEEE - 2010]
[AIEEE - 2010]
Ans. (3)
At t = 0 inductor behaves as broken wire then
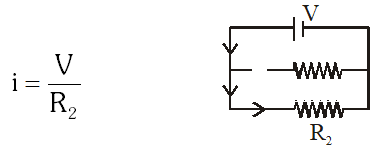 at $\mathrm{t}=\infty$ Inductor behaves as conducting wire
at $\mathrm{t}=\infty$ Inductor behaves as conducting wire
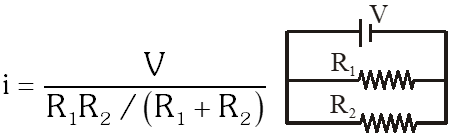
 at $\mathrm{t}=\infty$ Inductor behaves as conducting wire
at $\mathrm{t}=\infty$ Inductor behaves as conducting wire
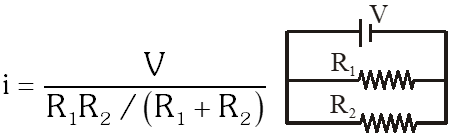
Q. A rectangular loop has a sliding connector PQ of length and resistance $\mathrm{R} \Omega$ and it is moving with a speed v as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents $\mathrm{I}_{1}, \mathrm{I}_{2}$ and I are :-
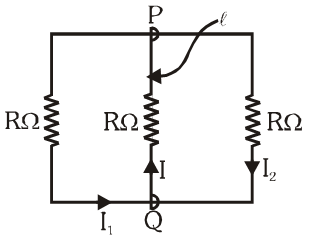 (1) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{6 \mathrm{R}}, \mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(2) $\mathrm{I}_{1}=-\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}, \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
(3) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}, \quad \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(4) $\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
[AIEEE - 2010]
(1) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{6 \mathrm{R}}, \mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(2) $\mathrm{I}_{1}=-\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}, \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
(3) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}, \quad \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(4) $\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
[AIEEE - 2010]
 (1) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{6 \mathrm{R}}, \mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(2) $\mathrm{I}_{1}=-\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}, \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
(3) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}, \quad \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(4) $\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
[AIEEE - 2010]
(1) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{6 \mathrm{R}}, \mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(2) $\mathrm{I}_{1}=-\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}, \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
(3) $\mathrm{I}_{1}=\mathrm{I}_{2}=\frac{\mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}, \quad \mathrm{I}=\frac{2 \mathrm{B} \ell \mathrm{v}}{3 \mathrm{R}}$
(4) $\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}=\frac{\mathrm{B} \ell \mathrm{v}}{\mathrm{R}}$
[AIEEE - 2010]
Ans. (3)
Circuit can be reduced as
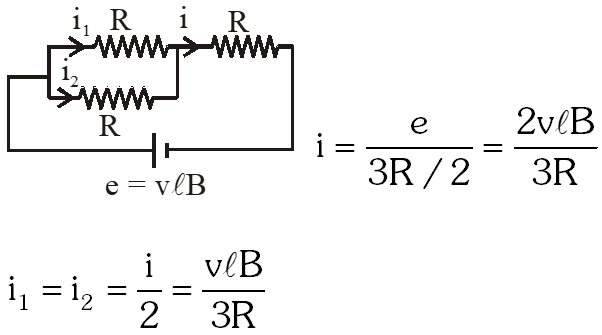
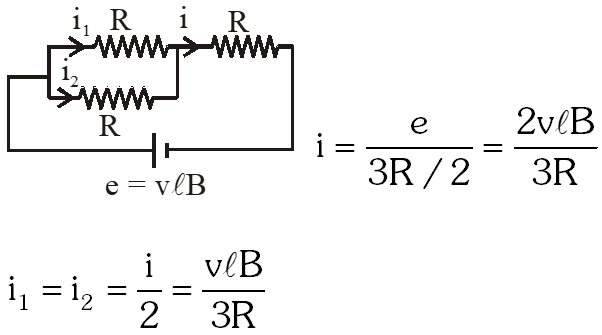
Q. A boat is moving due east in a region where the earth's magnetic field is 5.0×10–$^{5} \mathrm{NA}^{-1} \mathrm{m}^{-1}$ due north and horizontal. The boat carries a vertical aerial 2m long. If the speed of the boat is $1.50 \mathrm{ms}^{-1}$, the magnitude of the indueced emf in the wire of aerial is :-
(1) 0.50 mV
(2) 0.15 mV
(3) 1 mV
(4) 0.75 Mv
[AIEEE - 2011]
Ans. (2)
$e=\mathrm{B} \ell \mathrm{v}=\left(5 \times 10^{-5}\right)(2)(1.50)=0.15 \mathrm{mV}$
Q. A horizontal straight wire 20 m long extending from east to west is falling with a speed of 5.0 m/s, at right angles to the horizontal component of the earth's magnetic field 0.30 $\times 10^{-4}$$\mathrm{Wb} / \mathrm{m}^{2}$. The instantaneous value of the e.m.f. induced in the wire will be :-
(1) 6.0 mV
(2) 3 mV
(3) 4.5 mV
(4) 1.5 mV
[AIEEE - 2011]
Ans. (2)
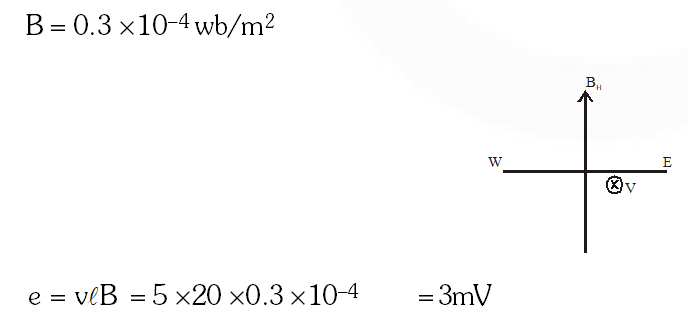
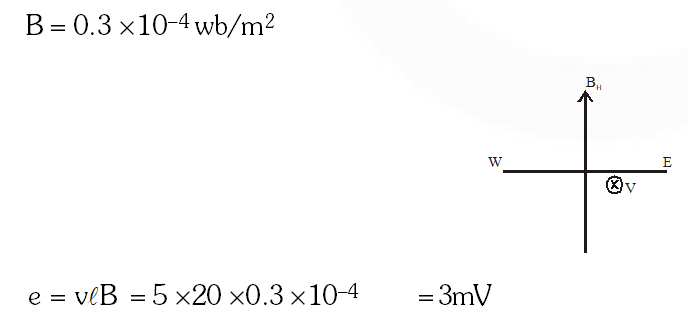
Q. A coil is suspended in a uniform magnetic field, with the plane of the coil parallel to the magnetic lines of force. When a current is passed through the coil it starts oscillating; it is very difficult to stop. But if an aluminium plate is placed near to the coil, it stops. This is due to :-
(1) Electromagnetic induction in the aluminium plate giving rise to electromagnetic damping
(2) Development of air current when the plate is placed
(3) Induction of electrical charge on the plate
(4) Shielding of magnetic lines of force as aluminium is a paramagnetic material
[AIEEE - 2012]
Ans. (1)
Due to conducting nature of Al eddy currents are produced
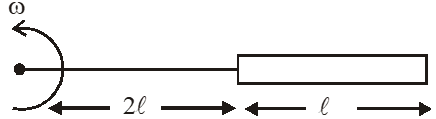
Q. A metallic rod of length 'l' is tied to a string of length 2l and made to rotate with angular speed $\omega$ on a horizontal table with one end of the string fixed. If there is a vertical magnetic field 'B' in the region, the e.m.f. induced across the ends of the rod is :
 (1) $\frac{2 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(2) $\frac{3 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(3) $\frac{4 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(4) $\frac{5 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
[JEE Main-2013]
(1) $\frac{2 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(2) $\frac{3 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(3) $\frac{4 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(4) $\frac{5 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
[JEE Main-2013]
 (1) $\frac{2 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(2) $\frac{3 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(3) $\frac{4 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(4) $\frac{5 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
[JEE Main-2013]
(1) $\frac{2 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(2) $\frac{3 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(3) $\frac{4 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
(4) $\frac{5 \mathrm{B} \omega \mathrm{l}^{2}}{2}$
[JEE Main-2013]
Ans. (4)
 E.M.F. induced $=\frac{1}{2} \mathrm{B} \omega\left[(3 \ell)^{2}-(2 \ell)^{2}\right]$
$=\frac{1}{2} \mathrm{B} \omega\left[5 \ell^{2}\right]$
$=\frac{5}{2} \mathrm{B} \omega \ell^{2}$
E.M.F. induced $=\frac{1}{2} \mathrm{B} \omega\left[(3 \ell)^{2}-(2 \ell)^{2}\right]$
$=\frac{1}{2} \mathrm{B} \omega\left[5 \ell^{2}\right]$
$=\frac{5}{2} \mathrm{B} \omega \ell^{2}$
 E.M.F. induced $=\frac{1}{2} \mathrm{B} \omega\left[(3 \ell)^{2}-(2 \ell)^{2}\right]$
$=\frac{1}{2} \mathrm{B} \omega\left[5 \ell^{2}\right]$
$=\frac{5}{2} \mathrm{B} \omega \ell^{2}$
E.M.F. induced $=\frac{1}{2} \mathrm{B} \omega\left[(3 \ell)^{2}-(2 \ell)^{2}\right]$
$=\frac{1}{2} \mathrm{B} \omega\left[5 \ell^{2}\right]$
$=\frac{5}{2} \mathrm{B} \omega \ell^{2}$
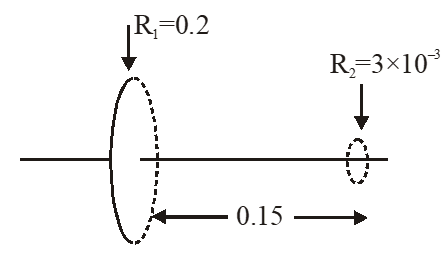
Q. A circular loop of radius 0.3 cm lies parallel to a much bigger circular loop of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with bigger loop is
(1) $9.1 \times 10^{-11}$ weber
(2) $6 \times 10^{-11}$ weber
(3) $3.3 \times 10^{-11}$ weber
(4) $6.6 \times 10^{-9}$ weber
[JEE Main-2013]
Ans. (1)
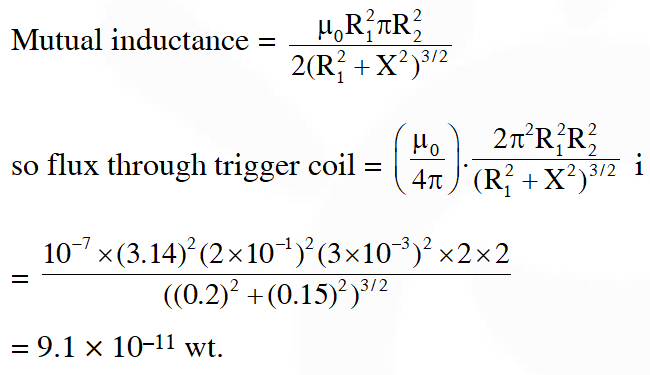

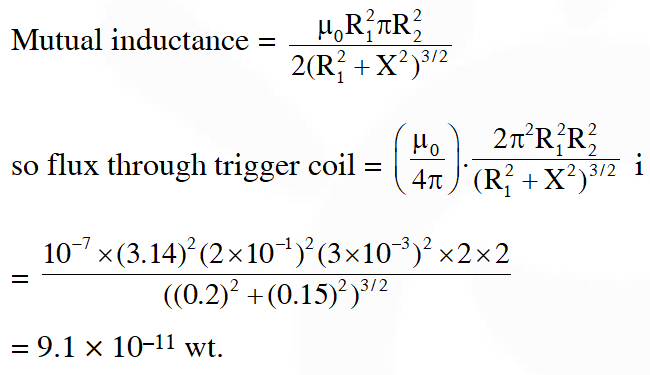
Q. In the circuit shown here, the point ‘C’ is kept connected to point ‘A’ till the current flowing through the circuit becomes constant. Afterward, suddenly, point ‘C’ is disconnected from point ‘A’ and connected to point ‘B’ at time t = 0. Ratio of the voltage across resistance and the inductor at t = L/R will be equal to :
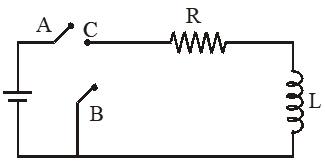 (1) –1
(2) $\frac{1-\mathrm{e}}{\mathrm{e}}$
(3) $\frac{\mathrm{e}}{1-\mathrm{e}}$
(4) 1
[JEE Main-2014]
(1) –1
(2) $\frac{1-\mathrm{e}}{\mathrm{e}}$
(3) $\frac{\mathrm{e}}{1-\mathrm{e}}$
(4) 1
[JEE Main-2014]
 (1) –1
(2) $\frac{1-\mathrm{e}}{\mathrm{e}}$
(3) $\frac{\mathrm{e}}{1-\mathrm{e}}$
(4) 1
[JEE Main-2014]
(1) –1
(2) $\frac{1-\mathrm{e}}{\mathrm{e}}$
(3) $\frac{\mathrm{e}}{1-\mathrm{e}}$
(4) 1
[JEE Main-2014]
Ans. (1)
$\mathrm{V}_{\mathrm{R}}+\mathrm{V}_{\mathrm{L}}=0$
$\frac{\mathrm{V}_{\mathrm{R}}}{\mathrm{V}_{\mathrm{L}}}=-1$
Q. An inductor (L = 0.03 H) and a resistor $(\mathrm{R}=0.15 \mathrm{k} \Omega)$ are connected in series to a battery of 15V EMF in a circuit shown below. The key $\mathrm{K}_{1}$ has been kept closed for a long time. Then at t = 0, $\mathbf{K}_{1}$ is opened and key K2 is closed simultaneously. At t = 1ms, the current in the circuit will be ($e^{5}$ 150):-
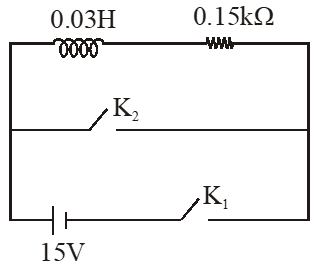 (1) 6.7 mA
(2) 0.67 mA
(3) 100 mA
(4) 67 mA
[JEE Main-2015]
(1) 6.7 mA
(2) 0.67 mA
(3) 100 mA
(4) 67 mA
[JEE Main-2015]
 (1) 6.7 mA
(2) 0.67 mA
(3) 100 mA
(4) 67 mA
[JEE Main-2015]
(1) 6.7 mA
(2) 0.67 mA
(3) 100 mA
(4) 67 mA
[JEE Main-2015]
Ans. (2)
Decay of current
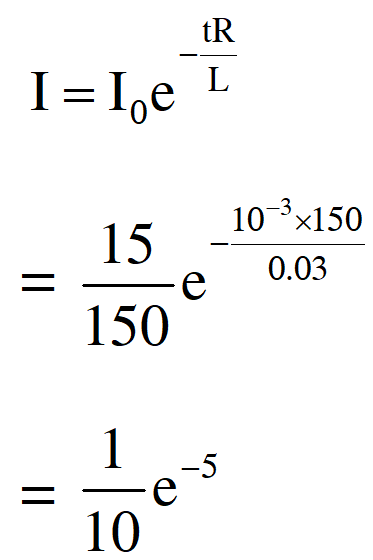
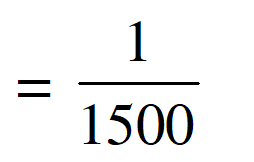 $=6.66 \times 10^{-4}$
$=0.666 \times 10^{-3}$
$=0.67 \mathrm{mA}$
$=6.66 \times 10^{-4}$
$=0.666 \times 10^{-3}$
$=0.67 \mathrm{mA}$
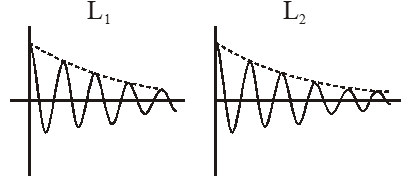
Q. An LCR circuit is equivalent to a damped pendulum. In an LCR circuit the capacitor is charged to $\mathrm{Q}_{0}$ and then connected to the L and R as shown below. If a student plots graphs of the square of maximum charge $\left(\mathrm{Q}_{\mathrm{Max}}^{2}\right)$ on the capacitor with time (t) for two different values $\mathrm{L}_{1}$ and $\mathrm{L}_{2}\left(\mathrm{L}_{1}\right.$ $\left.>\mathrm{L}_{2}\right)$ of L then which of the following represents this graph correctly ? (plots are schematic and not drawn to scale)
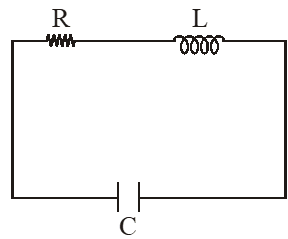
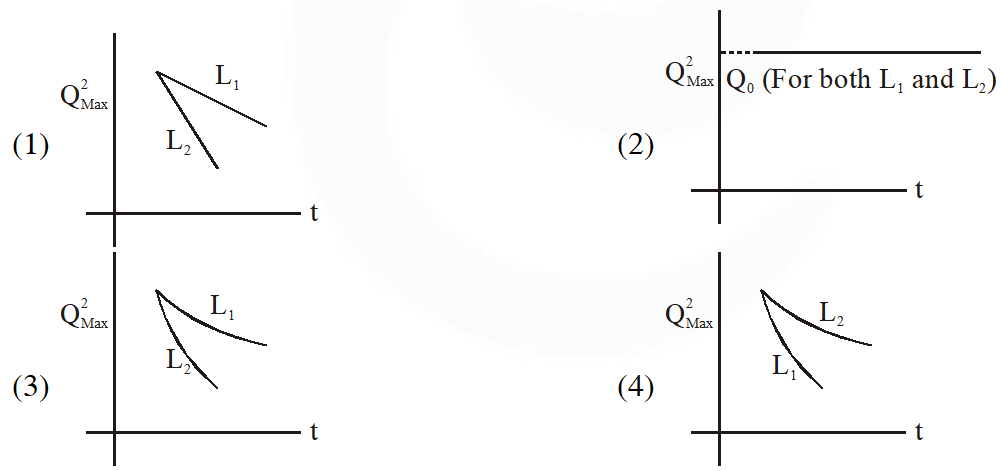 [JEE Main-2015]
[JEE Main-2015]

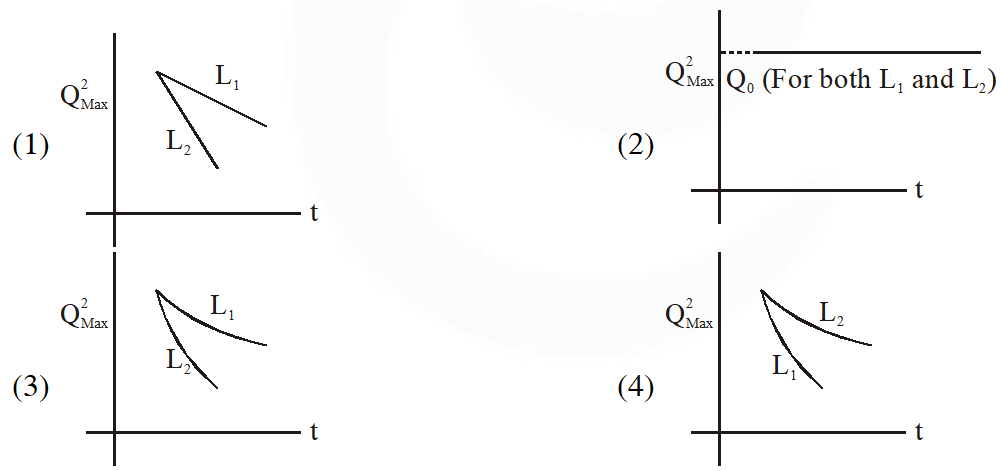 [JEE Main-2015]
[JEE Main-2015]
Ans. (3)
As damping is happening its amplitude would vary as
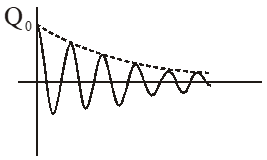 The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
$\therefore$ for
The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
$\therefore$ for
 The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
$\therefore$ for
The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
$\therefore$ for

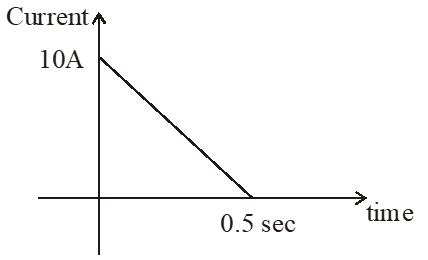
Q. In a coil of resistance $100 \Omega$, a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is :-
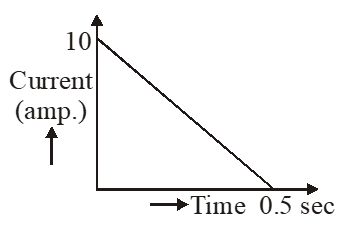 (1) 250 Wb
(2) 275 Wb
(3) 200 Wb
(4) 225 Wb
[JEE Advance-2017]
(1) 250 Wb
(2) 275 Wb
(3) 200 Wb
(4) 225 Wb
[JEE Advance-2017]
 (1) 250 Wb
(2) 275 Wb
(3) 200 Wb
(4) 225 Wb
[JEE Advance-2017]
(1) 250 Wb
(2) 275 Wb
(3) 200 Wb
(4) 225 Wb
[JEE Advance-2017]
Ans. (1)
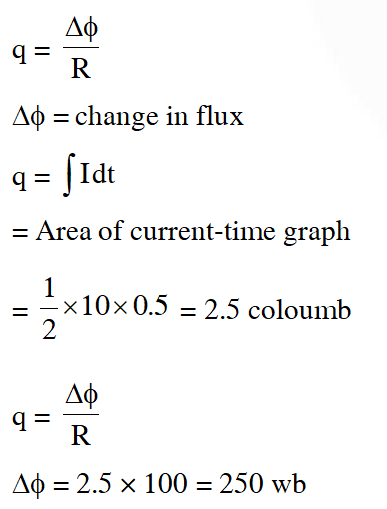

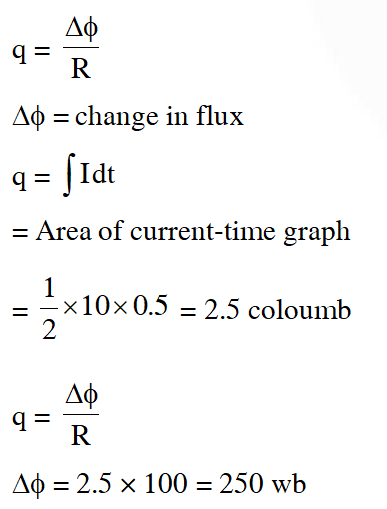
Comments
.
Feb. 12, 2021, 6:34 a.m.
Can you please give questions up-to 2020, because bits up-to 2015 is not enough for preparation of 2021
