JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. A charge Q is placed at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then $\frac{\mathrm{Q}}{\mathrm{q}}$ equals :-
(1) 1
$(2)-\frac{1}{\sqrt{2}}$
(3) $-2 \sqrt{2}$
(4) –1
[AIEEE - 2009]
Ans. (3)
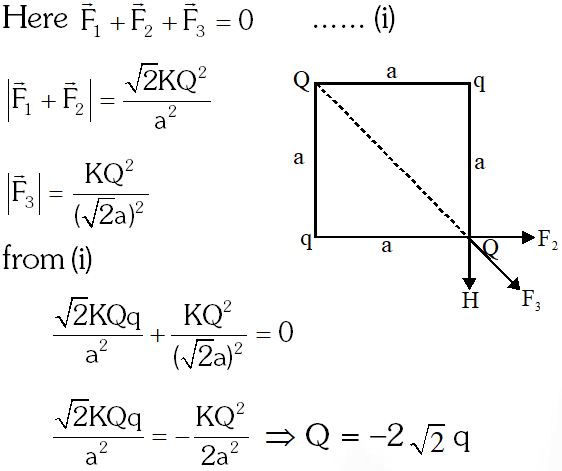
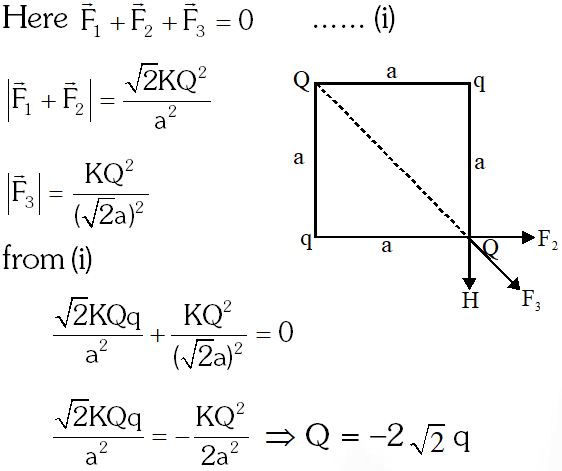
Q. Statement–1 : For a charged particle moving from point P to point Q the net work done by an electrostatic field on the particle is independent of the path connecting point P to point Q.
Statement–2 : The net work done by a conservative force on an object moving along closed loop is zero.
(1) Statement–1 is true, Statement–2 is true; Statement–2 is not the correct explanation of Statement–1
(2) Statement–1 is false, Statement–2 is true
(3) Statement–1 is true, Statement–2 is false
(4) Statement–1 is true, Statement–2 is true; Statement–2 is the correct explanation of Statement–
[AIEEE - 2009]
Ans. (4)
Electrostatics field is a conservative field work is independent of path.
Q. Two points P and Q are maintained at the potential of 10V and –4V, respectively. The work done in moving 100 electrons from P to Q is :-
(1) $-2.24 \times 10^{-16} \mathrm{J}$
(2) $2.24 \times 10^{-16} \mathrm{J}$
(3) $-9.60 \times 10^{-17} \mathrm{J}$
(4) $9.60 \times 10^{-17} \mathrm{J}$
[AIEEE - 2009]
Ans. (2)
$\mathrm{q}=-100 \times 1.6 \times 10^{-19} \mathrm{C}$
$\Delta \mathrm{V}=-14 \mathrm{volt}$z
$\mathrm{W}=\mathrm{q} \Delta \mathrm{V}=2.24 \times 10^{-16} \mathrm{J}$
Q. $\operatorname{Let} \mathrm{P}(\mathrm{r})=\frac{\mathrm{Q}}{\pi \mathrm{R}^{4}} \mathrm{r}$ be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance $r_{1}$ from the centre of the sphere, the magnitude of electric field is :-
(1) $\frac{\mathrm{Qr}_{1}^{2}}{4 \pi \epsilon_{0} \mathrm{R}^{4}}$
(2) $\frac{\mathrm{Qr}_{1}^{2}}{3 \pi \epsilon_{0} \mathrm{R}^{4}}$
(3) 0
(4) $\frac{\mathrm{Q}}{4 \pi \epsilon_{0} \mathrm{r}_{1}^{2}}$
[AIEEE - 2009]
Ans. (1)
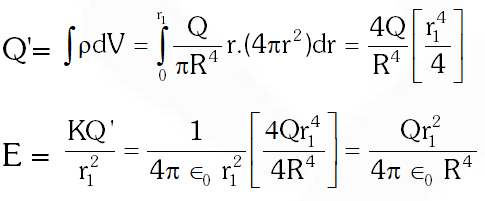
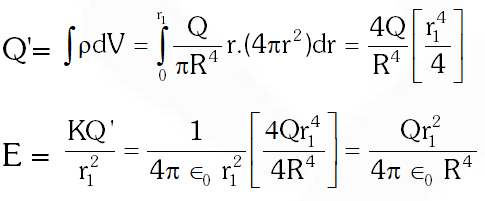
Q. A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field $\overrightarrow{\mathrm{E}}$ at the centre O is :-
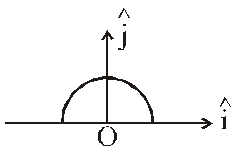 (1) $\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
( 2)$\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
$(3)-\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
(4) $-\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
[AIEEE - 2010]
(1) $\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
( 2)$\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
$(3)-\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
(4) $-\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
[AIEEE - 2010]
 (1) $\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
( 2)$\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
$(3)-\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
(4) $-\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
[AIEEE - 2010]
(1) $\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
( 2)$\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
$(3)-\frac{\mathrm{q}}{4 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
(4) $-\frac{\mathrm{q}}{2 \pi^{2} \varepsilon_{0} \mathrm{r}^{2}} \hat{\mathrm{j}}$
[AIEEE - 2010]
Ans. (4)
$\overrightarrow{\mathrm{E}}=\frac{2 \mathrm{k} \lambda}{\mathrm{r}}(-\hat{\mathrm{j}})=\frac{2}{\left(4 \pi \epsilon_{0} \mathrm{r}\right)} \frac{\mathrm{q}}{(\pi \mathrm{r})}(-\hat{\mathrm{j}})$
Q. Let there be a spherically symmetric charge distribution with charge density varying as
(r) = $\rho_{0}\left(\frac{5}{4}-\frac{\mathrm{r}}{\mathrm{R}}\right)$ upto r = R, and (r) = 0 for r > R, where r is the distance from the origin. The electric field at a distance r (r < R) from the origion is given by :
( 1)$\frac{\rho_{0} \mathrm{r}}{3 \varepsilon_{0}}\left(\frac{5}{4}-\frac{\mathrm{r}}{\mathrm{R}}\right)$
(2) $\frac{4 \pi \rho_{0} \mathrm{r}}{3 \varepsilon_{0}}\left(\frac{5}{3}-\frac{\mathrm{r}}{\mathrm{R}}\right)$
(3) $\frac{\rho_{0} \mathrm{r}}{4 \varepsilon_{0}}\left(\frac{5}{3}-\frac{\mathrm{r}}{\mathrm{R}}\right)$
(4) $\frac{4 \rho_{0} \mathrm{r}}{3 \varepsilon_{0}}\left(\frac{5}{4}-\frac{\mathrm{r}}{\mathrm{R}}\right)$
[AIEEE - 2010]
Ans. (3)
Total charge
$Q=\int_{0}^{r} \rho d V=\int_{0}^{r} \rho_{0}\left(\frac{5}{4}-\frac{r}{R}\right) 4 \pi r^{2} d r$
$=4 \pi \rho_{0} \int_{0}^{r}\left(\frac{5 r^{2}}{4}-\frac{r^{3}}{R}\right) d r=4 \pi \rho_{0}\left[\frac{5 r^{3}}{12}-\frac{r^{4}}{4 R}\right]$
$\mathrm{E}=\frac{\mathrm{KQ}}{\mathrm{r}^{2}}=\frac{1}{4 \pi \epsilon_{0} \mathrm{r}^{2}} 4 \pi \rho_{0}\left[\frac{5}{12} \mathrm{r}^{3}-\frac{\mathrm{r}^{4}}{4 \mathrm{R}}\right]$
$=\frac{\rho_{0} r}{4 \in_{0}}\left[\frac{5}{3}-\frac{r}{R}\right]$
Q. Two identical charged spheres suspended from a common point by two massless string of length $\ell$are initially a distance d(d << $\ell$) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity v. Then as a function of distance x between them :-
(1) $\mathrm{v} \propto \mathrm{x}^{1 / 2}$
(2) $\mathrm{v} \propto \mathrm{x}$
(3) $\mathrm{v} \propto \mathrm{x}^{-1 / 2}$
(4) $\mathrm{v} \propto \mathrm{x}^{-1}$
[AIEEE - 2011]
Ans. (3)
$\tan \theta=\frac{\mathrm{F}}{\mathrm{M}_{9}} \quad(\text { since } \theta \text { small })$
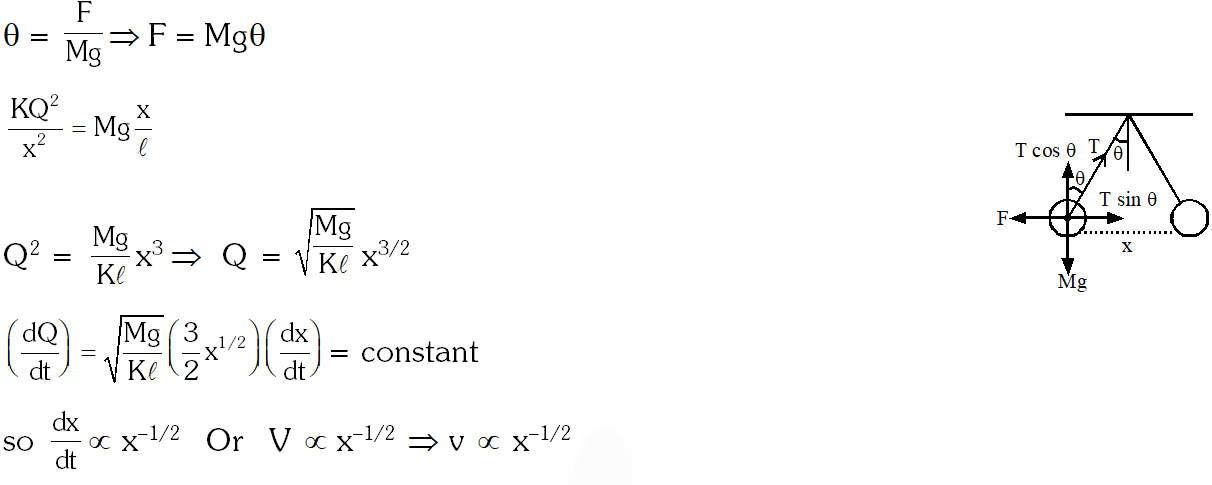
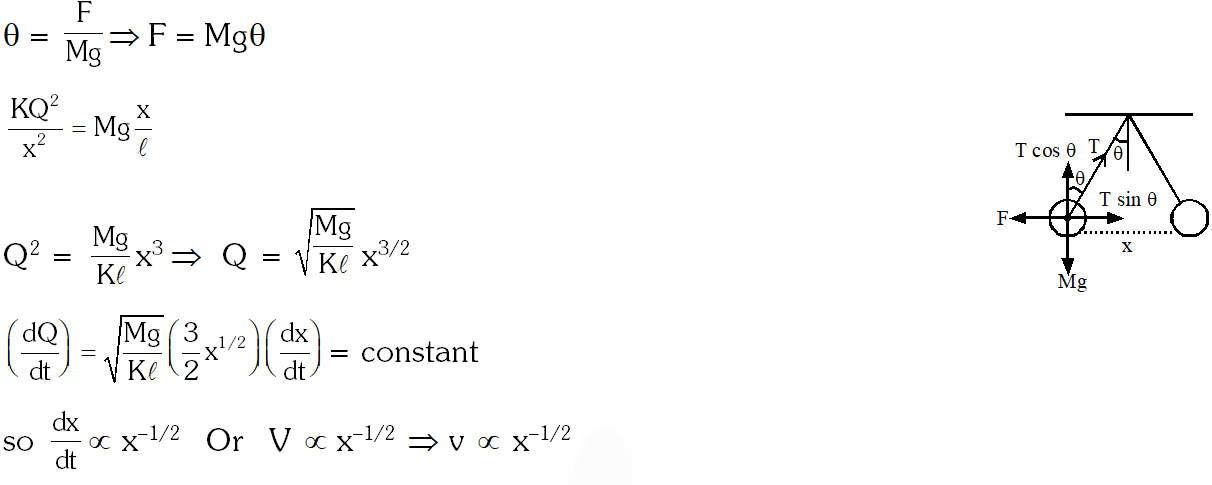
Q. The electrostatic potential inside a charged spherical ball is given by $\phi=\mathrm{ar}^{2}+\mathrm{b}$where r is the distance from the centre; a, b are constant. Then the charge density inside the ball is :-
(1) $-24 \pi \mathrm{a} \in_{0}$
$(2)-6 \mathrm{a} \in_{0}$
(3) $-24 \pi \mathrm{a} \in_{0} \mathrm{r}$
$(4)-6 \mathrm{a} \in_{0} \mathrm{r}$
[AIEEE - 2011]
Ans. (2)
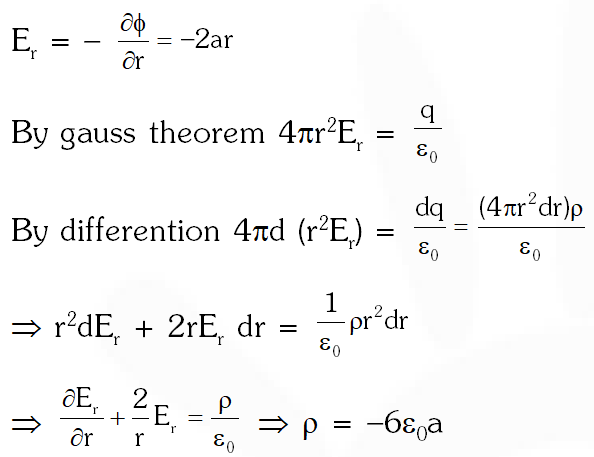
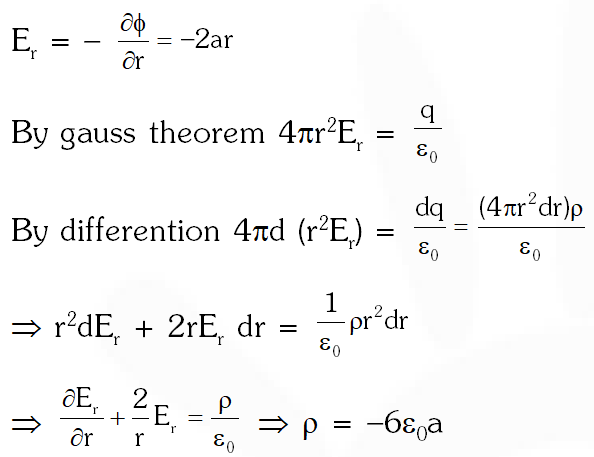
Q. Two positive charges of magnitude 'q' are placed at the ends of a side (side 1) of a square of side '2a'. Two negative charges of the same magnitude are kept at the other corners. Starting from rest, if a charge Q moves from the middle of side 1 to the centre of square, its kinetic energy at the centre of square is :-
(1) $\frac{1}{4 \pi \epsilon_{0}} \frac{2 \mathrm{qQ}}{\mathrm{a}}\left(1-\frac{1}{\sqrt{5}}\right)$
(2) zero
(3) $\frac{1}{4 \pi \epsilon_{0}} \frac{2 \mathrm{qQ}}{\mathrm{a}}\left(1+\frac{1}{\sqrt{5}}\right)$
(4) $\frac{1}{4 \pi \epsilon_{0}} \frac{2 \mathrm{qQ}}{\mathrm{a}}\left(1-\frac{2}{\sqrt{5}}\right)$
[AIEEE - 2011]
Ans. (1)
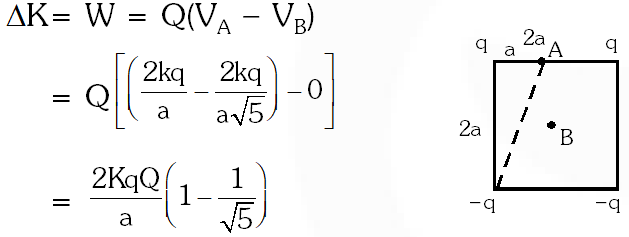
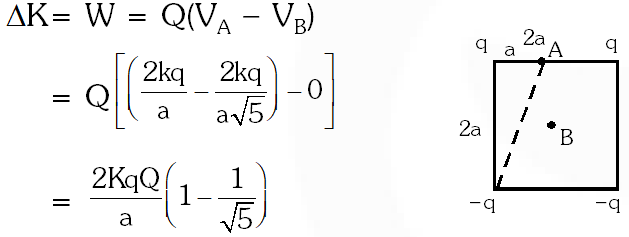
Q. This question has Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.
An insulating solid sphere of radius R has a uniformaly positive charge density . As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphre and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by $\frac{\mathrm{q} \rho}{3 \epsilon_{0}}$
Statement-2 : The electric field at a distance r (r < R) from the centre of the sphere is $\frac{\rho \mathrm{r}}{3 \epsilon_{0}}$
(1) Statement-1 is true, Statement-2 is true and Statement-2 is the correct explanation of
Statement-1.
(2) Statement-1 is true, Statement-2 is true and Statement-2 is not the correct explanation of
statement-1.
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is false, Statement-2 is true
[AIEEE - 2012]
Ans. (4)
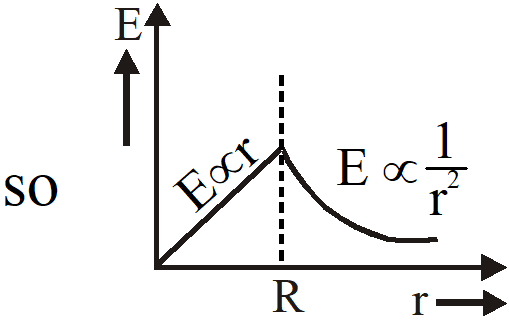
Q. In a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as a function of distance from the centre. The graph which would correspond to the above will be :-
 [AIEEE - 2012]
[AIEEE - 2012]
 [AIEEE - 2012]
[AIEEE - 2012]
Ans. (4)
For uniformly charged sphere
$\mathrm{E}=\frac{\mathrm{Kqr}}{\mathrm{R}^{3}}(\mathrm{r}<\mathrm{R})$
$\mathrm{E}=\frac{\mathrm{Kq}}{\mathrm{R}^{2}} \quad(\mathrm{r}=\mathrm{R})$
$\mathrm{E}=\frac{\mathrm{Kq}}{\mathrm{r}^{2}} \quad(\mathrm{r}>\mathrm{R})$

Q. Let $\left[\in_{0}\right]$ denote the dimensional formula of the permittivity of vacuum. If M = mass, L = Length,
T = Time and A = electric current, then :
(1) $\left[\in_{0}\right]=\left[\mathrm{M}^{-1} \mathrm{L}^{-3} \mathrm{T}^{2} \mathrm{A}\right]$
(2) $\left[\in_{0}\right]=\left[\mathrm{M}^{-1} \mathrm{L}^{-3} \mathrm{T}^{4} \mathrm{A}^{2}\right]$
(3) $\left[\in_{0}\right]=\left[\mathrm{M}^{-1} \mathrm{L}^{2} \mathrm{T}^{-1} \mathrm{A}^{-2}\right]$
(4) $\left[\in_{0}\right]=\left[\mathrm{M}^{-1} \mathrm{L}^{2} \mathrm{T}^{-1} \mathrm{A}\right]$
[AIEEE - 2013]
Ans. (2)
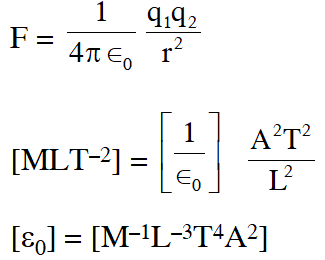
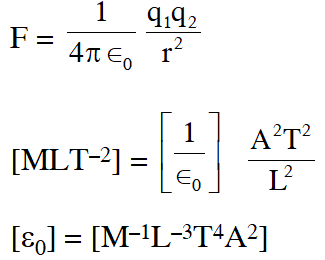
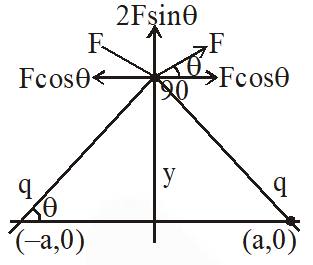
Q. Two charges, each equal to q, are kept at x = –a and x = a on the x-axis. A particle of mass m and charge $\mathrm{q}_{0}=\frac{\mathrm{q}}{2}$ is placed at the origin. If charge $q_{0}$ is given a small displacement (y << a) along the y-axis, the net force acting on the particle is proportional to
(1) y (2) –y (3) $\frac{1}{y}$ $ (4)-\frac{1}{\mathrm{y}}$
[AIEEE - 2013]
Ans. (1)
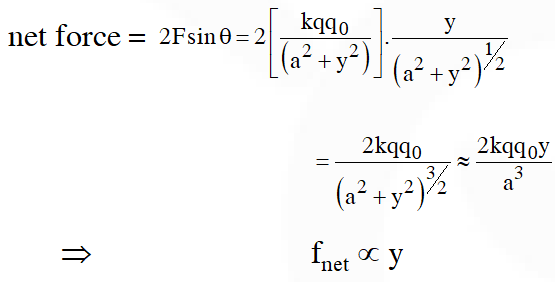

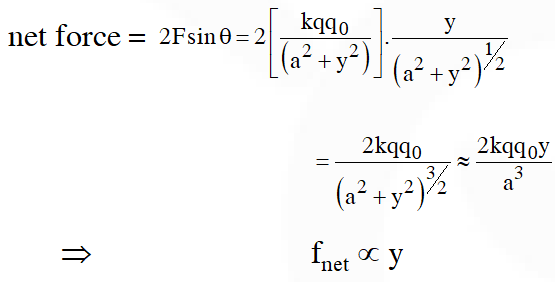
Q. A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at a distance L from the end A is :-
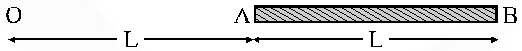 (1) $\frac{\mathrm{Q}}{8 \pi \epsilon_{0} \mathrm{L}}$
(2) $\frac{3 \mathrm{Q}}{4 \pi \in_{0} \mathrm{L}}$
(3) $\frac{\mathrm{Q}}{4 \pi \epsilon_{0} \mathrm{L} \ln 2}$
(4) $\frac{\mathrm{Q} \ln 2}{4 \pi \epsilon_{0} \mathrm{L}}$
[JEE-Main-2013]
(1) $\frac{\mathrm{Q}}{8 \pi \epsilon_{0} \mathrm{L}}$
(2) $\frac{3 \mathrm{Q}}{4 \pi \in_{0} \mathrm{L}}$
(3) $\frac{\mathrm{Q}}{4 \pi \epsilon_{0} \mathrm{L} \ln 2}$
(4) $\frac{\mathrm{Q} \ln 2}{4 \pi \epsilon_{0} \mathrm{L}}$
[JEE-Main-2013]
Ans. (4)
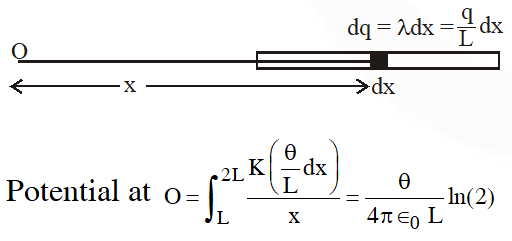
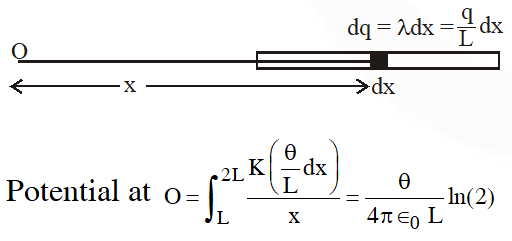
Q. Assume that an electric field $\overrightarrow{\mathrm{E}}=30 \mathrm{x}^{2} \hat{\mathrm{i}}$ exists in space. Then the potential difference $\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{\mathrm{O}}$, where $\mathrm{V}_{\mathrm{O}}$ is the potential at the origin and $\mathrm{V}_{\mathrm{A}}$ the potential at x = 2 m is :-
(1)–80 J
(2) 80 J
(3) 120 J
(4) –120 J
Ans. (1)
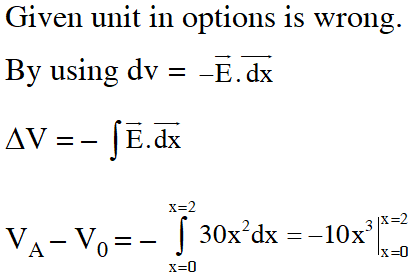 $\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{0}=-10[8-0]=-80 \mathrm{V}$
$\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{0}=-10[8-0]=-80 \mathrm{V}$
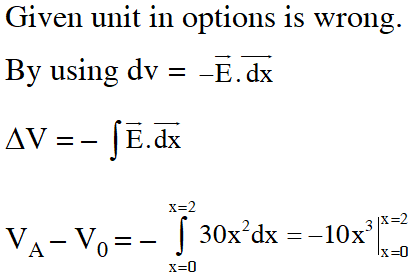 $\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{0}=-10[8-0]=-80 \mathrm{V}$
$\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{0}=-10[8-0]=-80 \mathrm{V}$
Q. The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), has volume charge density $\rho=\frac{\mathrm{A}}{\mathrm{r}}$, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :-
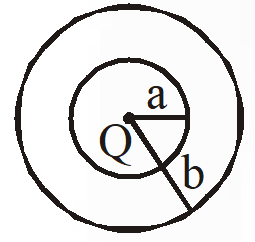 (1) $\frac{2 Q}{\pi a^{2}}$
(2) $\frac{\mathrm{Q}}{2 \pi \mathrm{a}^{2}}$
(3) $\frac{\mathrm{Q}}{2 \pi\left(\mathrm{b}^{2}-\mathrm{a}^{2}\right)}$
(4) $\frac{2 \mathrm{Q}}{\pi\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}$
[JEE-Main-2016]
(1) $\frac{2 Q}{\pi a^{2}}$
(2) $\frac{\mathrm{Q}}{2 \pi \mathrm{a}^{2}}$
(3) $\frac{\mathrm{Q}}{2 \pi\left(\mathrm{b}^{2}-\mathrm{a}^{2}\right)}$
(4) $\frac{2 \mathrm{Q}}{\pi\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}$
[JEE-Main-2016]
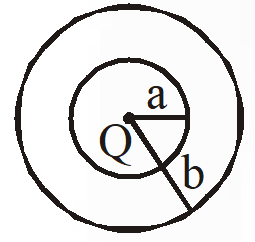 (1) $\frac{2 Q}{\pi a^{2}}$
(2) $\frac{\mathrm{Q}}{2 \pi \mathrm{a}^{2}}$
(3) $\frac{\mathrm{Q}}{2 \pi\left(\mathrm{b}^{2}-\mathrm{a}^{2}\right)}$
(4) $\frac{2 \mathrm{Q}}{\pi\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}$
[JEE-Main-2016]
(1) $\frac{2 Q}{\pi a^{2}}$
(2) $\frac{\mathrm{Q}}{2 \pi \mathrm{a}^{2}}$
(3) $\frac{\mathrm{Q}}{2 \pi\left(\mathrm{b}^{2}-\mathrm{a}^{2}\right)}$
(4) $\frac{2 \mathrm{Q}}{\pi\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}$
[JEE-Main-2016]
Ans. (2)
Gaussian surface at distance r from center
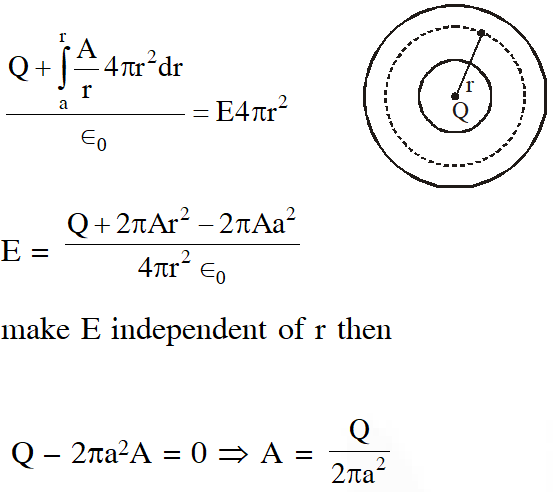
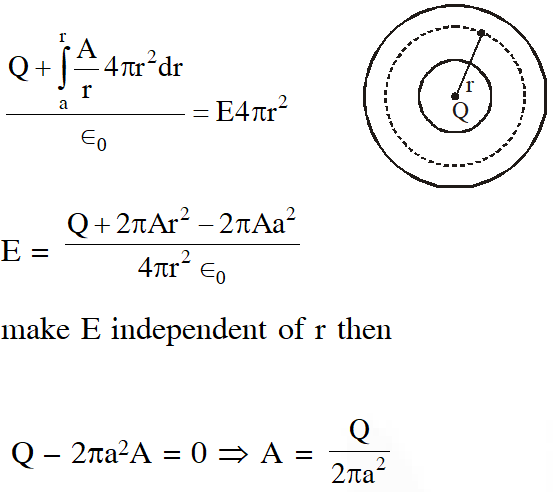
Q. An electric dipole has a fixed dipole moment $\overrightarrow{\mathrm{p}}$, which makes angle with respect to x-axis. When subjected to an electric field $\overrightarrow{\mathrm{E}}_{1}=\mathrm{E} \hat{\mathrm{i}}$, it experiences a torque $\overrightarrow{\mathrm{T}}_{1}=\tau \hat{\mathrm{k}}$. When subjected to another electric field $\overrightarrow{\mathrm{E}}_{2}=\sqrt{3} \mathrm{E}_{1} \hat{\mathrm{j}}$ it experiences torque . The angle $\theta$ is :
(1) $60^{\circ}$ (2) $90^{\circ}$ (3) $30^{\circ}$ (4) $45^{\circ}$
[JEE-Main-2017]
Ans. (1)
So from $\quad \vec{\tau}=\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{E}}$
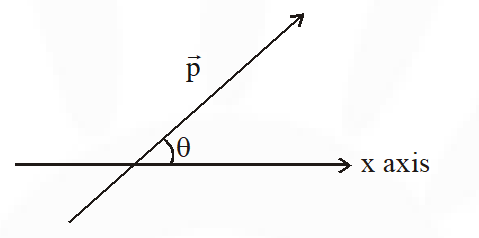
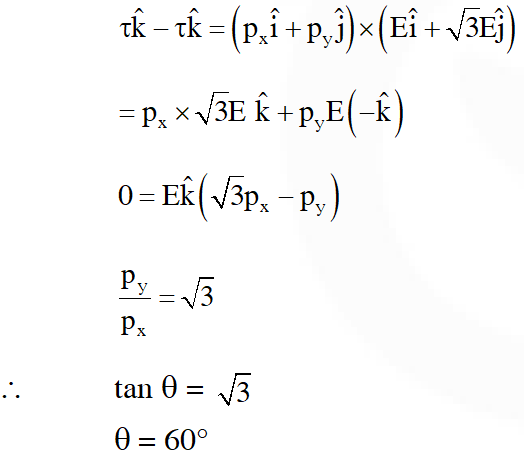
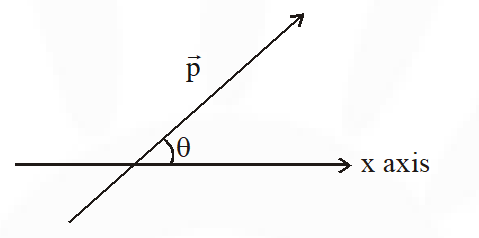
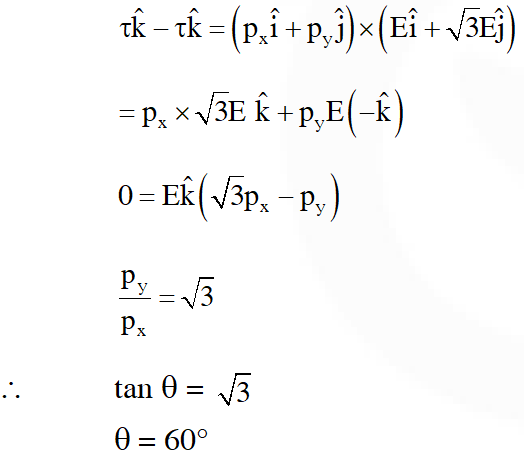
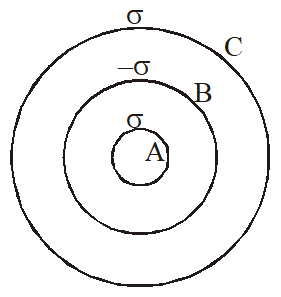
Q. Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge densities $+\sigma,-\sigma$ and $+\sigma$ respectively. The potential of shell B is :-
 [JEE-Main-2018]
[JEE-Main-2018]
 [JEE-Main-2018]
[JEE-Main-2018]
Ans. (1)

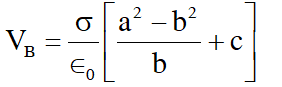


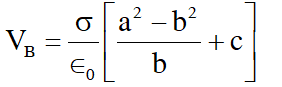
Comments
Marshall
Feb. 10, 2024, 6:35 a.m.
Wow, amazing weblog format! How lengthy have you been blogging for?
you make running a blog look easy. The whole glance of your site is fantastic, as well as the
content! You can see similar: Bestero.shop and here Bestero.shop
MUSKAAN MEHROTRA
Nov. 22, 2020, 3:52 p.m.
APPRECIATION; THANKU SO MUCH, It was really helpful for me. :>
REQUEST: Plz.... upload chapter wise segregated questions from 2019 and 2020 jee papers.
BEFORE JEE MAINS 2021 JANUARY.
Anam Bushra Granger
Aug. 19, 2020, 12:04 p.m.
The best site for solving questions because it gives time to solve without displaying the answer directly and provide very explaining solution
Rahul
Aug. 17, 2020, 6:05 p.m.
thank u esaral ,,,,,it was very helpful......hope to get such helps in upcoming days also,,,
De-morgan markonikov
May 25, 2020, 8:10 p.m.
Awesome work.E Saral will soon be one of the best online platform for competitive exams
harsha
May 3, 2020, 8:48 p.m.
Thank you so much sir it's so much useful
But I think that AIEEE 2010 solution was wrong and the process would be by taking Gaussian surface
