JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Tangents are drawn from the point $\mathrm{P}(3,4)$ to the ellipse $\frac{\mathrm{x}^{2}}{9}+\frac{\mathrm{y}^{2}}{4}=1$ touching the ellipse at points A and B
Let $\mathrm{F}_{1}\left(\mathrm{x}_{1}, 0\right)$ and $\mathrm{F}_{2}\left(\mathrm{x}_{2}, 0\right)$ for $\mathrm{x}_{1}<0$ and $\mathrm{x}_{2}>0,$ be the foci of the ellipse $\frac{\mathrm{x}^{2}}{9}+\frac{\mathrm{y}^{2}}{8}=1 .$ Suppose a parabola having vertex at the origin and focus at $\mathrm{F}_{2}$ intersects the ellipse at point $\mathrm{M}$ in the first quadrant and at point $\mathrm{N}$ in the fourth quadrant.
Q. The line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse $x^{2}+9 y^{2}=9$ meets its auxiliary circle at the point M. Then the area of the triangle with vertices at A, M and the origin O is
(A) $\frac{31}{10}$
(B) $\frac{29}{10}$
(C) $\frac{21}{10}$
(D) $\frac{27}{10}$
[JEE 2009, 3]
Ans. (D)
Area of triangle $\mathrm{AOM}=\frac{1}{2} \mathrm{AO} . \mathrm{PM}$
$\Rightarrow$ Eqaution of $\mathrm{AM}$ is $\mathrm{y}=\frac{1}{3}(\mathrm{x}+3)$
$\mathrm{x}-3 \mathrm{y}+3=0$ which is chord of auxiliary circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9$
and $\mathrm{PM}$ is ordinate of point $\mathrm{M}$
$\Rightarrow(3 \mathrm{y}-3)^{2}+\mathrm{y}^{2}=9 \Rightarrow \mathrm{y}=\frac{9}{5}=\mathrm{PM}$
$2 \cos \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right) \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=4 \sin ^{2} \frac{\mathrm{A}}{2} \Rightarrow \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \sin \frac{\mathrm{A}}{2}$
$\Rightarrow 2 \cos \frac{\mathrm{A}}{2} \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \cdot 2 \sin \frac{\mathrm{A}}{2} \cdot \cos \frac{\mathrm{A}}{2} \Rightarrow 2 \sin \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right) \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \sin \mathrm{A}$
$\Rightarrow \sin \mathrm{B}+\sin \mathrm{C}=2 \sin \mathrm{A}$
$\Rightarrow \mathrm{b}+\mathrm{c}=2 \mathrm{a}$
$\Rightarrow$ locus is ellipse
Q. The normal at a point $P$ on the ellipse $x^{2}+4 y^{2}=16$ meets the $x$ -axis at $Q .$ If $M$ is the mid point of the line segment $P Q$, then the locus of Mintersects the latus rectums of the given ellipse at the point
(A) $\left(\pm \frac{3 \sqrt{5}}{2}, \pm \frac{2}{7}\right)$
(B) $\left(\pm \frac{3 \sqrt{5}}{2}, \pm \frac{\sqrt{19}}{4}\right)$
(C) $\left(\pm 2 \sqrt{3}, \pm \frac{1}{7}\right)$
(D) $\left(\pm 2 \sqrt{3}, \pm \frac{4 \sqrt{3}}{7}\right)$
[JEE 2009, 3]
Ans. (C)
Q. In a triangle PQR, let $\angle \mathrm{PQR}=30^{\circ}$ and the sides $\mathrm{PQ}$ and $\mathrm{QR}$ have lengths $10 \sqrt{3}$ and 10 , respectively. Then, which of the following statement(s) is (are) TRUE?
(A) $\angle \mathrm{QPR}=45^{\circ}$
(B) The area of the triangle PQR is $25 \sqrt{3}$ and $\angle \mathrm{QRP}=120^{\circ}$
(C) The radius of the incircle of the triangle PQR is $10 \sqrt{3}-15$
(D) The area of the circumcircle of the triangle PQR is $100 \pi$.
Ans. (B,C,D)
$2 \cos \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right) \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=4 \sin ^{2} \frac{\mathrm{A}}{2} \Rightarrow \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \sin \frac{\mathrm{A}}{2}$
$\Rightarrow 2 \cos \frac{\mathrm{A}}{2} \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \cdot 2 \sin \frac{\mathrm{A}}{2} \cdot \cos \frac{\mathrm{A}}{2} \Rightarrow 2 \sin \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right) \cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=2 \sin \mathrm{A}$
$\Rightarrow \sin \mathrm{B}+\sin \mathrm{C}=2 \sin \mathrm{A}$
$\Rightarrow \mathrm{b}+\mathrm{c}=2 \mathrm{a}$
$\Rightarrow$ locus is ellipse.
Comprehension: $4 \mathrm{to} 5$
Q. The coordinates of A and B are
(A) (3,0) and (0,2)
(B) $\left(-\frac{8}{5}, \frac{2 \sqrt{261}}{15}\right)$ and $\left(-\frac{9}{5}, \frac{8}{5}\right)$
(C) $\left(-\frac{8}{5}, \frac{2 \sqrt{161}}{15}\right)$ and $(0,2)$
(D) $(3,0)$ and $\left(-\frac{9}{5}, \frac{8}{5}\right)$
[JEE 2010, 3+3+3]
Ans. (D)
Q. The orthocenter of the triangle PAB is
(A) $\left(5, \frac{8}{7}\right)$
(B) $\left(\frac{7}{5}, \frac{25}{8}\right)$
(C) $\left(\frac{11}{5}, \frac{8}{5}\right)$
(D) $\left(\frac{8}{25}, \frac{7}{5}\right)$
Ans. (C)
Q. The equation of the locus of the point whose distances from the point P and the line AB are equal, is –
(A) $9 x^{2}+y^{2}-6 x y-54 x-62 y+241=0$
(B) $x^{2}+9 y^{2}+6 x y-54 x+62 y-241=0$
(C) $9 x^{2}+9 y^{2}-6 x y-54 x-62 y-241=0$
(D) $x^{2}+y^{2}-2 x y+27 x+31 y-120=0$
Ans. (A)
Equation of line $\mathrm{AB}$ is $\mathrm{x}+3 \mathrm{y}=3$
Now let the point be $(\mathrm{h}, \mathrm{k})$
According to question,
$\left|\frac{h+3 k-3}{\sqrt{1^{2}+3^{2}}}\right|=\sqrt{(h-3)^{2}+(4-k)^{2}}$
After solving, we get
$9 x^{2}+y^{2}-6 x y-54 x-62 y+241=0$
Q. The ellipse $\mathrm{E}_{1}: \frac{\mathrm{x}^{2}}{9}+\frac{\mathrm{x}^{2}}{4}=1$ is inscribed in a rectangle $\mathrm{R}$ whose sides are parallel to the coordinate axes. Another ellipse $\mathrm{E}_{2}$ passing through the point $(0,4)$ circumscribes the rectangle $\mathrm{R}$. The eccentricity of the ellipse $\mathrm{E}_{2}$ is $-$
(A) $\frac{\sqrt{2}}{2}$
(B) $\frac{\sqrt{3}}{2}$
(C) $\frac{1}{2}$
(D) $\frac{3}{4}$
[JEE 2012, 3M, –1M]
Ans. (C)
Q. A vertical line passing through the point (h,0) intersects the ellipse $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$ at the points $P$ and $Q$. Let the tangents to the ellipse at $P$ and $Q$ meet at the point $R .$ If $\Delta(h)=$ area of the triangle $P Q R, \Delta_{1}=\max _{1 / 2 \leq h \leq 1} \Delta(h)$ and $\Delta_{2}=\min _{1 / 2 \Delta \operatorname{Lh} \leq 1} \Delta(h),$ then $\frac{8}{\sqrt{5}} \Delta_{1}-8 \Delta_{2}=$
[JEE-Advanced 2013, 4, (–1)]
Ans. (9)
Q.
[JEE(Advanced)-2014, 3(–1)]
[JEE(Advanced)-2014, 3(–1)]
Ans. (A)
Q. Suppose that the foci of the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$ are $\left(f_{1}, 0\right)$ and $\left(f_{2}, 0\right)$ where $f_{1}>0$ and $f_{2}<0 .$ Let $\mathrm{P}_{1}$ and $\mathrm{P}_{2}$ be two parabolas with a common vertex at $(0,0)$ and with foci at $\left(f_{1}, 0\right)$ and $\left(2 f_{2}, 0\right),$ respectively. Let $\mathrm{T}_{1}$ be a tangent to $\mathrm{P}_{1}$ which passes through $\left(2 f_{2}, 0\right)$ and $\mathrm{T}_{2}$ be a tangent to $\mathrm{P}_{2}$ which passes through $\left(f_{1}, 0\right) .$ If $\mathrm{m}_{1}$ is the slope of $\mathrm{T}_{1}$ and $\mathrm{m}_{2}$ is the slope of $\mathrm{T}_{2},$ then the value of
$\left(\frac{1}{\mathrm{m}_{1}^{2}}+\mathrm{m}_{2}^{2}\right)$ is
[JEE 2015, 4M, –0M]
Ans. 4
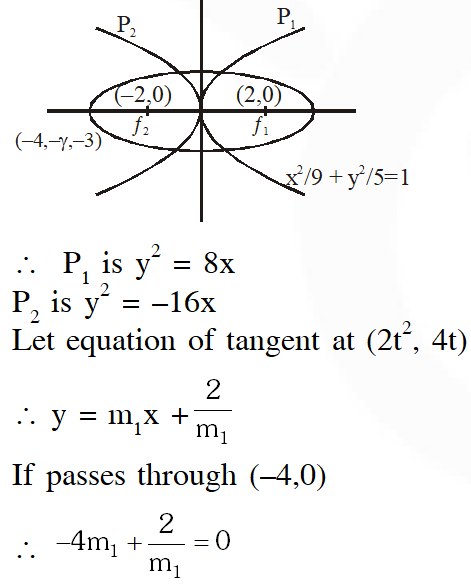
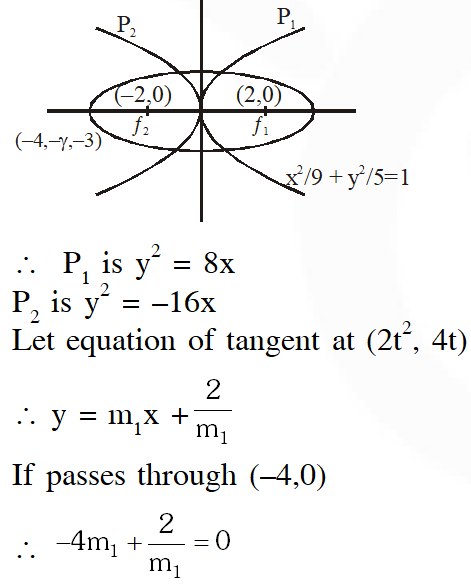
Q. Let $\mathrm{E}_{1}$ and $\mathrm{E}_{2}$ be two ellipses whose centers are at the origin. The major axes of $\mathrm{E}_{1}$ and $\mathrm{E}_{2}$ lie along the $\mathrm{x}$ -axis and the $\mathrm{y}$ -axis, respectively. Let $\mathrm{S}$ be the circle $\mathrm{x}^{2}+(\mathrm{y}-1)^{2}=2 .$ The straight line $\mathrm{x}+\mathrm{y}=3$ touches the curves $\mathrm{S}, \mathrm{E}_{1}$ and $\mathrm{E}_{2}$ at $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R},$ respectively. Suppose that $\mathrm{PQ}=\mathrm{PR}=\frac{2 \sqrt{2}}{3} .$ If $\mathrm{e}_{1}$ and $\mathrm{e}_{2}$ are the eccentricities of $\mathrm{E}_{1}$ and $\mathrm{E}_{2},$ respectively, then the correct expression(s) is(are)
(A) $\mathrm{e}_{1}^{2}+\mathrm{e}_{2}^{2}=\frac{43}{40}$
(B) $\mathrm{e}_{1} \mathrm{e}_{2}=\frac{\sqrt{7}}{2 \sqrt{10}}$
(C) $\left|\mathrm{e}_{1}^{2}-\mathrm{e}_{2}^{2}\right|=\frac{5}{8}$
(D) $\mathrm{e}_{1} \mathrm{e}_{2}=\frac{\sqrt{3}}{4}$
[JEE 2015, 4M, –0M]
Ans. (A,B)
Let $\mathrm{E}_{1}: \frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{b}^{2}}=1 \quad(\mathrm{a}>\mathrm{b})$
$\mathrm{\&} \quad \mathrm{E}_{2}: \frac{\mathrm{x}^{2}}{\mathrm{c}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{d}^{2}}=1 \quad(\mathrm{c}<\mathrm{d})$
$\& \quad \mathrm{S}: \mathrm{x}^{2}+(\mathrm{y}-1)^{2}=2$
$\mathrm{\&} \quad$ tangent to $\mathrm{E}_{1}, \mathrm{E}_{2} \& \mathrm{S}$ is $\mathrm{x}+\mathrm{y}=3$
Now, point of contact of $\mathrm{S} \&$ tangent is $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$
Let $\mathrm{x}=\mathrm{X} \quad \& \mathrm{y}-1=\mathrm{Y}$
$\therefore \quad \mathrm{X}^{2}+\mathrm{Y}^{2}=2$
$\mathrm{\&} \quad \mathrm{X}+\mathrm{Y}=2$
Let $\left(\mathrm{X}_{1}, \mathrm{Y}_{1}\right)$ be point of contact.
$\therefore \quad \mathrm{X}_{1}+\mathrm{YY}_{1}=2$
$\therefore \quad \mathrm{X}_{1}=1 \& \mathrm{Y}_{1}=1$
$\therefore \quad \mathrm{x}_{1}=1 \& \mathrm{y}_{1}=2$
Now, parametric equation of $x+y=3$
is $\frac{x-1}{-\frac{1}{\sqrt{2}}}=\frac{y-2}{\frac{1}{\sqrt{2}}}=\pm \frac{2 \sqrt{2}}{3} \Rightarrow x=\frac{5}{3}, y=\frac{4}{3}$
$\Rightarrow \quad x=\frac{1}{3} \& y=\frac{8}{3}$
$\therefore \quad \mathrm{P} \equiv(1,2), \quad \mathrm{Q} \equiv\left(\frac{5}{3}, \frac{4}{3}\right) \quad \& \quad \mathrm{R}=\left(\frac{1}{3}, \frac{8}{3}\right)$
Now, equation tangent at $\mathrm{Q}$ on ellipse $\mathrm{E}_{1}$
$\frac{\mathrm{x} \cdot 5}{3 \mathrm{a}^{2}}+\frac{\mathrm{y} \cdot 4}{3 \mathrm{b}^{2}}=1$
Comparing it with $\mathrm{x}+\mathrm{y}=3$
$\therefore \quad \mathrm{a}^{2}=5 \& \mathrm{b}^{2}=4$
Now, $e_{1}^{2}=1-\frac{4}{5}=\frac{1}{5}$
Similarly, $e_{2}^{2}=\frac{7}{8}$
$\therefore \quad e_{1}^{2} e_{2}^{2}=\frac{7}{40} \Rightarrow e_{1} e_{2}=\frac{\sqrt{7}}{2 \sqrt{10}}$
$e_{1}^{2}+e_{2}^{2}=\frac{1}{5}+\frac{7}{8}=\frac{43}{40} ; \quad\left|e_{1}^{2}-e_{2}^{2}\right|=\left|\frac{1}{5}-\frac{7}{8}\right|=\frac{27}{40}$
$\therefore \quad(A) \&(B)$
Q. The orthocentre of the triangle $F_{1} \mathrm{MN}$ is-
(A) $\left(-\frac{9}{10}, 0\right)$
(B) $\left(\frac{2}{3}, 0\right)$
(C) $\left(\frac{9}{10}, 0\right)$
(D) $\left(\frac{2}{3}, \sqrt{6}\right)$
[JEE 2015, 4M, –0M]
Ans. (A)
Orthocentre lies on $\mathrm{x}$ -axis
Equation of altitude through $\mathrm{M}: \mathrm{y}-\sqrt{6}=\frac{5}{2 \sqrt{6}}\left(\mathrm{x}-\frac{3}{2}\right)$
Equation of altitude through $\mathrm{F}_{1}: \mathrm{y}=0$
solving, we get orthocentre $\left(-\frac{9}{10}, 0\right)$
Orthocentre lies on $\mathrm{x}$ -axis
Equation of altitude through $\mathrm{M}: \mathrm{y}-\sqrt{6}=\frac{5}{2 \sqrt{6}}\left(\mathrm{x}-\frac{3}{2}\right)$
Equation of altitude through $\mathrm{F}_{1}: \mathrm{y}=0$
solving, we get orthocentre $\left(-\frac{9}{10}, 0\right)$
Q. If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral $\mathrm{MF}_{1} \mathrm{NF}_{2}$ is-
(A) 3 : 4 (B) 4 : 5 (C) 5 : 8 (D) 2 : 3
[JEE(Advanced)-2016]
Ans. (C)
Normal to parabola at $\mathrm{M}: \mathrm{y}-\sqrt{6}=-\frac{\sqrt{6}}{2.1}\left(\mathrm{x}-\frac{3}{2}\right)$
Solving it with $\mathrm{y}=0,$ we get $\mathrm{Q} \equiv\left(\frac{7}{2}, 0\right)$
Tangent to ellipse at $M: \frac{x \cdot \frac{3}{2}}{9}+\frac{y(\sqrt{6})}{8}=1$
Solving it with $y=0$, we get $R \equiv(6,0)$
$\therefore$ Area of triangle MQR $=\frac{1}{2} \cdot\left(6-\frac{7}{2}\right) \cdot \sqrt{6}=\frac{5 \sqrt{6}}{4}$
Area of quadrilateral $\mathrm{MF}_{1} \mathrm{NF}_{2}=2 \cdot \frac{1}{2} \cdot(1-(-1)) \cdot \sqrt{6}=2 \sqrt{6}$
Required ratio $=5: 8$
Normal to parabola at $\mathrm{M}: \mathrm{y}-\sqrt{6}=-\frac{\sqrt{6}}{2.1}\left(\mathrm{x}-\frac{3}{2}\right)$
Solving it with $\mathrm{y}=0,$ we get $\mathrm{Q} \equiv\left(\frac{7}{2}, 0\right)$
Tangent to ellipse at $M: \frac{x \cdot \frac{3}{2}}{9}+\frac{y(\sqrt{6})}{8}=1$
Solving it with $y=0$, we get $R \equiv(6,0)$
$\therefore$ Area of triangle MQR $=\frac{1}{2} \cdot\left(6-\frac{7}{2}\right) \cdot \sqrt{6}=\frac{5 \sqrt{6}}{4}$
Area of quadrilateral $\mathrm{MF}_{1} \mathrm{NF}_{2}=2 \cdot \frac{1}{2} \cdot(1-(-1)) \cdot \sqrt{6}=2 \sqrt{6}$
Required ratio $=5: 8$
Q. Consider two straight lines, each of which is tangent to both the circle $x^{2}+y^{2}=\frac{1}{2}$ and the parabola $\mathrm{y}^{2}=4 \mathrm{x}$. Let these lines intersect at the point Q. Consider the ellipse whose center is at the origin O(0, 0) and whose semi-major axis is OQ. If the length of the minor axis of this ellipse is $\sqrt{2}$, then the which of the following statement(s) is (are) TRUE ?
(A) For the ellipse, the eccentricity is $\frac{1}{\sqrt{2}}$ and the length of the latus rectum is 1
(B) For the ellipse, the eccentricity is $\frac{1}{2}$ and the length of the latus rectum is $\frac{1}{2}$
(C) The area of the region bounded by the ellipse between the lines $\mathrm{x}=\frac{1}{\sqrt{2}}$ and $\mathrm{x}=1$ is $\frac{1}{4 \sqrt{2}}(\pi-2)$
(D) The area of the region bounded by the ellipse between the lines $x=\frac{1}{\sqrt{2}}$ and $x=1$ is $\frac{1}{16}(\pi-2)$
[JEE(Advanced)-2016]
Ans. (A,C)
Let equation of common tangent is $\mathrm{y}=\mathrm{mx}+\frac{1}{\mathrm{m}}$
$\therefore \quad\left|\frac{0+0+\frac{1}{\mathrm{m}}}{\sqrt{1+\mathrm{m}^{2}}}\right|=\frac{1}{\sqrt{2}} \Rightarrow \mathrm{m}^{4}+\mathrm{m}^{2}-2=0 \Rightarrow \mathrm{m}=\pm 1$
Equation of common tangents are $\mathrm{y}=\mathrm{x}+1$ and $\mathrm{y}=-\mathrm{x}-1$
point $\mathrm{Q}$ is $(-1,0)$
$\therefore$ Equation of ellipse is $\frac{\mathrm{x}^{2}}{1}+\frac{\mathrm{y}^{2}}{1 / 2}=1$
(A) $\mathrm{e}=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$ and $\mathrm{LR}=\frac{2 \mathrm{b}^{2}}{\mathrm{a}}=1$
Area $2 . \int_{1 / \sqrt{2}}^{1} \frac{1}{\sqrt{2}} \cdot \sqrt{1-x^{2}} d x=\sqrt{2}\left[\frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} \sin ^{-1} x\right]_{1 / \sqrt{2}}^{1}$
$=\sqrt{2}\left[\frac{\pi}{4}-\left(\frac{1}{4}+\frac{\pi}{8}\right)\right]=\sqrt{2}\left(\frac{\pi}{8}-\frac{1}{4}\right)=\frac{\pi-2}{4 \sqrt{2}}$
correct answer are (A) and (D)
Let equation of common tangent is $\mathrm{y}=\mathrm{mx}+\frac{1}{\mathrm{m}}$
$\therefore \quad\left|\frac{0+0+\frac{1}{\mathrm{m}}}{\sqrt{1+\mathrm{m}^{2}}}\right|=\frac{1}{\sqrt{2}} \Rightarrow \mathrm{m}^{4}+\mathrm{m}^{2}-2=0 \Rightarrow \mathrm{m}=\pm 1$
Equation of common tangents are $\mathrm{y}=\mathrm{x}+1$ and $\mathrm{y}=-\mathrm{x}-1$
point $\mathrm{Q}$ is $(-1,0)$
$\therefore$ Equation of ellipse is $\frac{\mathrm{x}^{2}}{1}+\frac{\mathrm{y}^{2}}{1 / 2}=1$
(A) $\mathrm{e}=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$ and $\mathrm{LR}=\frac{2 \mathrm{b}^{2}}{\mathrm{a}}=1$
Area $2 . \int_{1 / \sqrt{2}}^{1} \frac{1}{\sqrt{2}} \cdot \sqrt{1-x^{2}} d x=\sqrt{2}\left[\frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} \sin ^{-1} x\right]_{1 / \sqrt{2}}^{1}$
$=\sqrt{2}\left[\frac{\pi}{4}-\left(\frac{1}{4}+\frac{\pi}{8}\right)\right]=\sqrt{2}\left(\frac{\pi}{8}-\frac{1}{4}\right)=\frac{\pi-2}{4 \sqrt{2}}$
correct answer are (A) and (D)