JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph "A"
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation z = x/y. If the errors in x, y and z are $\Delta \mathrm{x}, \Delta \mathrm{y}$ and $\Delta \mathrm{z}$, respectively, then
$z \pm \Delta z=\frac{x \pm \Delta x}{y \pm \Delta y}=\frac{x}{y}\left(1 \pm \frac{\Delta x}{x}\right)\left(1 \pm \frac{\Delta y}{y}\right)^{-1}$
The series expansion for $\left(1 \pm \frac{\Delta y}{y}\right)^{-1}$, to first power in y/y, is $1 \mp(\Delta y / y) .$ The relative errors in independent variables are always added. So the error in z will be
$\Delta z=z\left(\frac{\Delta x}{x}+\frac{\Delta y}{y}\right)$
The above derivation makes the assumption that $\frac{\Delta x}{x}<<1, \frac{\Delta y}{y}<<1$. Therefore, the higher powers of these quantities are neglected.
(There are two questions based on Paragraph "A", the question given below is one of them)
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation z = x/y. If the errors in x, y and z are $\Delta \mathrm{x}, \Delta \mathrm{y}$ and $\Delta \mathrm{Z}$, respectively, then
$z \pm \Delta z=\frac{x \pm \Delta x}{y \pm \Delta y}=\frac{x}{y}\left(1 \pm \frac{\Delta x}{x}\right)\left(1 \pm \frac{\Delta y}{y}\right)^{-1}$
The series expansion for $\left(1 \pm \frac{\Delta y}{y}\right)^{-1},$ to first power in $\Delta y / y,$ is $1 \mp(\Delta y / y) .$ The relative errors in independent variables are always added. So the error in z will be
The above derivation makes the assumption that $\frac{\Delta x}{x}<<1, \frac{\Delta y}{y}<<1 .$ Therefore, the higher powers of these quantities are neglected.
(There are two questions based on Paragraph "A", the question given below is one of them)
Q. A student uses a simple pendulum of exactly 1m length to determine g, the acceleration due to gravity. He uses a stopwatch with the least count of 1 sec for this and records 40 seconds for 20 oscillations. For this observation, which of the following statement(s) is (are) true?
(A) Error T in measuring T, the time period is 0.05 seconds
(B) Error T in measuring T, the time period is 1 second
(C) Percentage error in the determination of g is 5%
(D) Percentage error in the determination of g is 2.5%
[JEE 2010]
Ans. (A,C)
$\mathrm{T}_{\mathrm{A}}=\mathrm{T}_{\mathrm{B}} \Rightarrow$ Internal energies are equal and work done in process $\mathrm{AB}=\mathrm{P}_{0} \mathrm{V}_{0} \ell \mathrm{n}\left(\frac{4 \mathrm{V}_{0}}{\mathrm{V}_{0}}\right)=$ $\mathrm{P}_{0} \mathrm{V}_{0} \ell \mathrm{n}(4)$
Note : Had the process BC been isobaric then answer would have been (ABCD). But the question does not clearly indicate whether BC passes through origin or NOT.
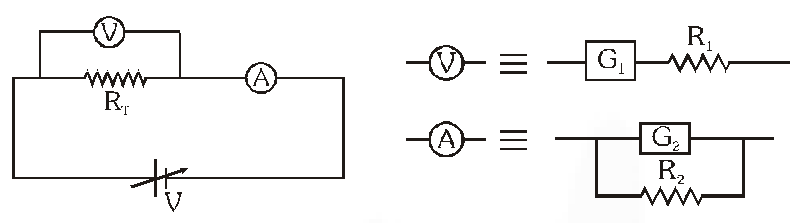
Q. To verify Ohm’s law, a student is provided with a test resistor $\mathrm{R}_{\mathrm{T}}$, a high resistance $\mathrm{R}_{1}$, a small resistance $\mathrm{R}_{2}$, two identical galvanometers $\mathrm{G}_{1}$ and $\mathrm{G}_{2}$ , and a variable voltage source V. The correct circuit to carry out the experiment is :–
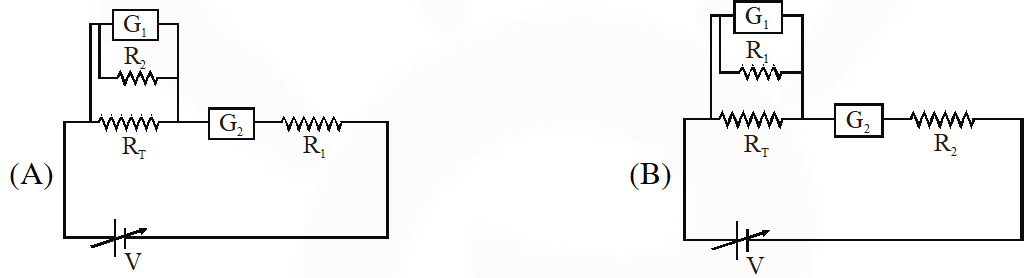
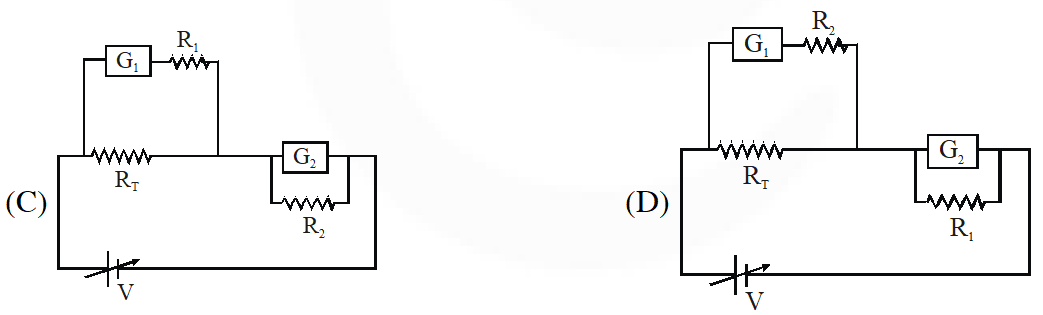[JEE 2010]
[JEE 2010]
Ans. (C)
Q. A Vernier callipers has 1 mm marks on the main scale. It has 20 equal divisions on the Vernier scale which match with 16 main scale divisions. For this Vernier calipers, the least count is –
(A) 0.02 mm (B) 0.05 mm (C) 0.1 mm (D) 0.2 mm
[JEE 2010]
Ans. (D)
$\mathrm{LC}=\mathrm{a}\left[1-\frac{\mathrm{m}}{\mathrm{n}}\right]=1 \mathrm{mm}\left[1-\frac{16}{20}\right]=1 \mathrm{mm}[0.2]=0.2 \mathrm{mm}$
Q. A meter bridge is set-up as shown, to determine an unknown resistance ‘X’ using a standard 10 ohm resistor. The galvanometer shows point when tapping-key is at 52 cm mark. The
end-corrections are 1 cm and 2 cm respectively for the ends A and B. The determined value of ‘X’ is –
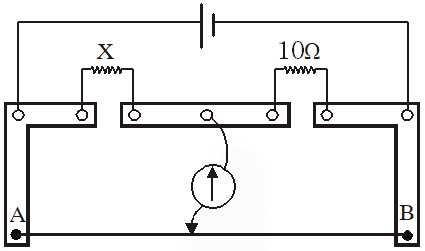(A) 10.2 ohm (B) 10.6 ohm (C) 10.8 ohm (D) 11.1 ohm
[JEE 2011]
(A) 10.2 ohm (B) 10.6 ohm (C) 10.8 ohm (D) 11.1 ohm
[JEE 2011]
Ans. (B)
Apply condition of wheatstone bridge, $\frac{x}{52+1}=\frac{10}{48+2} \Rightarrow x=\frac{10}{50} \times 53 \Rightarrow \mathrm{x}=10.6 \Omega$
Q. The density of a solid ball is to be determined in an experiment. The diameter of the ball is measured with a screw gauge, whose pitch is 0.5 mm and there are 50 divisions on the circular scale. The reading on the main scale is 2.5 mm and that on the circular scale is 20 divisions. If the measured mass of the ball has a relative error of 2%, the relative percentage error in the density is –
(A) 0.9% (B) 2.4% (C) 3.1% (D) 4.2%
[JEE 2011]
Ans. (C)
$P=\frac{M}{\frac{4}{3} \pi r^{3}}, 100 \times \frac{\Delta P}{P}=\left(\frac{\Delta M}{M}+\frac{3 \Delta r}{r}\right) \times 100$
$\Delta \mathrm{r}=$ least count $=0.01 \Rightarrow \mathrm{r}=2.70$
$\frac{\Delta P}{P} \times 100=2 \%+\left(3 \times \frac{0.01}{2.70}\right) \times 100=3.1 \%$
Q. In the determination of Young's modulus $\left(Y=\frac{4 M L g}{\pi \ell d^{2}}\right)$ by using Searle's method, a wire of length L = 2m and diameter d = 0.5 mm is used. For a load M = 2.5 kg, an extension l = 0.25 mm in the length of the wire is observed. Quantities d and l are measured using a screw gauge and a micrometer, respectively. They have the same pitch of 0.5 mm. The number of divisions on their circular scale is 100. The contributions to the maximum probable error of the Y measurement
[JEE 2012]
Ans. (A)
$y=\frac{4 M L g}{\pi \ell d^{2}} \Rightarrow \frac{\delta y}{y}=\frac{\delta(\ell)}{\ell}+\frac{2 \delta(d)}{d}$
$\frac{\delta \ell}{\ell}=\frac{[0.5 / 100]}{0.25}=\frac{1}{50}$ and $\frac{2 \delta(d)}{d}=\frac{2[0.5 / 100]}{0.5}=\frac{1}{50}$
Q. The diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero of the Vernier scale lies between 5.10 cm and 5.15 cm of the main scale. The Vernier scale has 50 divisions equivalent to 2.45 cm. The 24th division of the Vernier scale excatly coincides with one of the main scale divisions. The diameter of the cylinder is :-
(A) 5.112 cm (B) 5.124 cm (C) 5.136 cm (D) 5.148 cm
[JEE 2013]
Ans. (B)
50 divisions $=2.45 \mathrm{cm}$
$\Rightarrow 1$ division $=\frac{2.45}{50}=0.049 \mathrm{cm}$
$\Rightarrow 1$ east count $=1 \mathrm{MSD}-1 \mathrm{VSD}=0.05-0.049=0.001 \mathrm{cm}$
So vernier reading $=0.001 \times 24=0.024 \mathrm{cm} .$
Therefore diameter of cylinder
$=5.10+0.024=5.124 \mathrm{cm} .$
Q. Using the expression 2d sin $\theta$ = $\lambda$, one calculates the values of d by measuring the corresponding angles $\theta$ in the range 0 to $90^{\circ}$. The wavelength $\lambda$ is exactly known and the error in $\theta$ is constant for all values of $\theta$. As $\theta$ increases from $0^{\circ}$ :-
(A) the absolute error in d remains constant
(B) the absolute error in d increases
(C) the fractional error in d remains constant
(D) the fractional error in d decreases
[JEE-Advance 2013]
Ans. (D)
$d=\frac{\lambda}{2 \sin \theta}$
$\delta(\mathrm{d})=\left(\frac{\lambda}{2 \sin ^{2} \theta}\right) \cos \theta \delta \theta \quad\{\delta \theta=\mathrm{constant}\}$
as $\theta$ increases, $\frac{\cos \theta}{\sin ^{2} \theta}$ decreases so
Absolute error $|\delta(\mathrm{d})|$ decreases
Also fractional error
$=\left|\frac{\delta(\mathrm{d})}{\mathrm{d}}\right|=\frac{\left(\frac{\lambda \cos \theta}{2 \sin ^{2} \theta}\right) \delta \theta}{\frac{\lambda}{2 \sin \theta}}=(\cot \theta) \delta \theta$
as $\theta$ increases, $\cot \theta$ decreases, so fractional error decreases
Q. During Searle's experiment, zero of the Vernier scale lies between $3.20 \times 10^{-2}$ m and $3.25 \times 10^{-2}$ m of the main scale. The 20th division of the Vernier scale exactly coincides with one of the main scale divisions. When an additional load of 2 kg is applied to the wire, the zero of the Vernier scale still lies between $3.20 \times 10^{-2}$ m and $3.25 \times 10^{-2}$ m of the main scale but now the 45th division of Vernier scale coincides with one of the main scale divisions. The length of the thin metallic wire is 2m and its cross-sectional area is $8 \times 10^{-7} \mathrm{m}^{2}$. The least count of the Vernier scale is $1.0 \times 10^{-5}$ m. The maximum percentage error in the Young's modulus of the wire is.
[JEE-Advance 2014]
Ans. 4
For meter bridge,
$\mathrm{R}=\mathrm{X}\left(\frac{\ell}{100-\ell}\right)=90\left(\frac{\ell}{100-\ell}\right)=90\left(\frac{40}{60}\right)$
$=60 \Omega$
error in R : (erro = least count)
$\frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}=\frac{\mathrm{dx}}{\mathrm{x}}+\frac{\mathrm{d} \ell}{\ell}+\frac{\mathrm{d}(100-\ell)}{(100-\ell)}=0+\frac{\operatorname{lmm}}{40 \mathrm{cm}}+\frac{1 \mathrm{mm}}{60 \mathrm{cm}}$
$\frac{\mathrm{d} \mathrm{R}}{60 \Omega}=\frac{1}{4} \Rightarrow \mathrm{d} \mathrm{R}=0.25 \Omega$
$\mathrm{R}=6 \pm 0.25 \Omega$
Q. Consider a Vernier callipers in which each 1 cm on the main scale is divided into 8 equal divisions and a screw gauge with 100 divisions on its circular scale. In the Vernier callipers, 5 divisions of the Vernier scale coincide with 4 divisions on the main scale and in the screw gauge, one complete rotation of the circular scale moves it by two divisions on the linear scale. Then :
(A) If the pitch of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.01 mm.
(B) If the pitch of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.005 mm.
(C) If the least count of the linear scale of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.01 mm.
(D) If the least count of the linear scale of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.005 mm.
[JEE-Advance 2015]
Ans. (B,C)
1 main scale division $(\mathrm{M} . \mathrm{S} . \mathrm{D} .)=\frac{1}{8} \mathrm{cm}$
5 veriner scale division (V.S.D.) = 4 M.S.
$1 \mathrm{V} . \mathrm{S.D.}=\frac{4}{5} \mathrm{M} . \mathrm{S.D}$
Least count of vernier scale (L.C.) = 1 M.S.D. – 1 V.S.D.
$=1 \mathrm{M} . \mathrm{S.D.}-\frac{4}{5} \mathrm{M} . \mathrm{S.D}$
$(\mathrm{L.C})=\frac{1 \mathrm{MS.D.}}{5}=\frac{1}{40} \mathrm{cm}$
For option A and B
If the pitch of the screw gauge is twice the least count of the vernier callipers then
pitch = 2 × L.C of vernier scale
$=\frac{1}{20} \mathrm{cm}$
hence least count of screw gauge $=\frac{\text { Pitch }}{100}$
= 0.005 m
For option C and D
Least count of linear scale of screw gauge
$=2 \times \frac{1}{40}=\frac{1}{20} \mathrm{cm}$
Pitch $=2 \times \frac{1}{20}=\frac{1}{10} \mathrm{cm}=1 \mathrm{mm}$
Least count of screw gauge $=\frac{1 \mathrm{mm}}{100}=0.01 \mathrm{mm}$
Hence answer is (B,C)
Q. The energy of a system as a function of time t is given as E(t) = $\mathrm{A}^{2}$ exp $(-\alpha t)$ , where $\alpha=0.2 \mathrm{s}^{-1}$ . The measurement of A has an error of 1.25%. If the error in the measurement of time is 1.50%, the percentage error in the value of E(t) at t = 5 s is -
[JEE-Advance 2015]
Ans. 4
Energy $\mathrm{E}=\mathrm{A}^{2} \mathrm{e}^{-\alpha \mathrm{t}}$
for small % errors, we can, do differentiation
$\mathrm{dE}=2 \mathrm{A}(\mathrm{d} \mathrm{A}) \mathrm{e}^{-\alpha \mathrm{t}}+\mathrm{A}^{2}\left(-\alpha \mathrm{e}^{-\alpha \mathrm{t}} \mathrm{dt}\right)$
fractional error $=\frac{\mathrm{dE}}{\mathrm{E}}=\frac{2 \mathrm{Ae}^{-\alpha \mathrm{t}}(\mathrm{d} \mathrm{A})+\left(-\alpha \mathrm{A}^{2} \mathrm{e}^{-\alpha \mathrm{t}}\right) \mathrm{dt}}{\mathrm{A}^{2} \mathrm{e}^{-\alpha \mathrm{t}}}=2\left(\frac{\mathrm{d} \mathrm{A}}{\mathrm{A}}\right)+\left(-\alpha \frac{\mathrm{dt}}{\mathrm{t}}\right) \mathrm{t}$
% error = 2(1.25%) + (0.2 × 1.5%) × 5
= 4% (errors always add up)
Alternate Sol.
$\mathrm{E}=\mathrm{A}^{2} \mathrm{e}^{-\alpha \mathrm{t}}$
taking natural logarithm on both sides,
$\ln (\mathrm{E})=\ln \left(\mathrm{A}^{2}\right)+(-\alpha \mathrm{t})$
Differentiating
$\frac{\mathrm{dE}}{\mathrm{E}}=2\left(\frac{\mathrm{d} \mathrm{A}}{\mathrm{A}}\right)+(-\alpha \mathrm{dt})$
for small fractional erros, errors always add up
$\left|\frac{\mathrm{dE}}{\mathrm{E}}\right|=2\left|\frac{\mathrm{d} \mathrm{A}}{\mathrm{A}}\right|+\alpha\left(\frac{\mathrm{dt}}{\mathrm{t}}\right) \times \mathrm{t}$
= 2(1.25%) + (0.2)(1.5%)5
= 4%
Q. There are two vernier calipers both of which have $1 \mathrm{cm}$ divided into 10 equal divisions on the main scale. The Vernier scale of the calipers $\left(\mathrm{C}_{1}\right)$ has $10 \mathrm{equal}$ divisions that correspond to 9 main scale divisions. The Vernier scale of the other caliper $\left(\mathrm{C}_{2}\right)$ has 10 equal divisions that correspond to 11 main scale divisions. The readings of the two calipers are shown in the figure. The measured values (in $\mathrm{cm}$ ) by calipers $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ respectively, are :
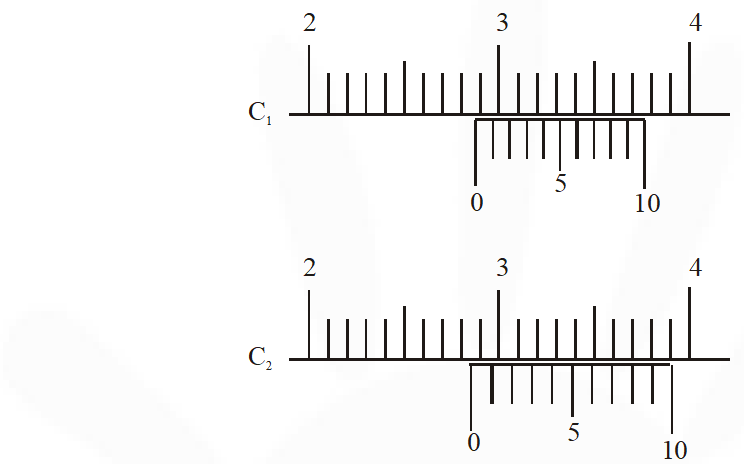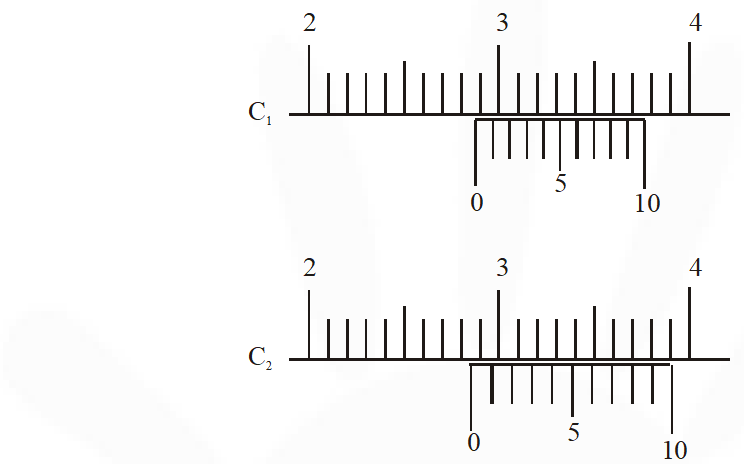(A) 2.87 and 2.86 (B) 2.87 and 2.87 (C) 2.87 and 2.83 (D) 2.85 and 2.82
[JEE-Advance 2016]
(A) 2.87 and 2.86 (B) 2.87 and 2.87 (C) 2.87 and 2.83 (D) 2.85 and 2.82
[JEE-Advance 2016]
Ans. (C)
For caliper $\mathrm{C}_{1}$
10 VSD = 9MSD
LC = 1MSD – 1VSD
LC = 0.01 cm
Measured value = Main scale reading + vernier scale readin
= (2.8 + 7 × 0.01) cm
= 2.87 cm
For Caliper $\mathrm{C}_{2}$
10 VSD = 11 MSD
LC = 0.01 cm
Measured value = {2.8 + (10–7) × 0.01}cm
= 2.83 cm
Q. In an experiment to determine the acceleration due to gravity g, the formula used for the time period of a periodic motion is $\mathrm{T}=2 \pi \sqrt{\frac{7(\mathrm{R}-\mathrm{r})}{5 \mathrm{g}}}$. The values of R and r are measured to be $(60 \pm 1) \operatorname{mm}$ and $(10 \pm 1)$ mm, respectively. In five successive measurements, the time period is found to be0.52 s, 0.56 s, 0.57s, 0.54 s and 0.59 s. The least count of the watch used for the measurement of time period is 0.01 s. Which of the following statement(s) is(are) true ?
(A) The error in the measurement of r is 10%
(B) The error in the measurement of T is 3.57 %
(C) The error in the measurement of T is 2%
(D) The error in the determined value of g is 11%
[JEE-Advance 2016]
Ans. (A,B,D)
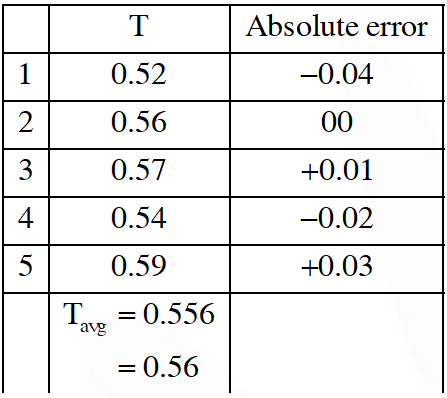Avg. absolute error $=\frac{.04+00+.01+.02+.03}{5}=.02$
$\Rightarrow \frac{\Delta \mathrm{T}}{\mathrm{T}} \times 100 \%=\frac{.02}{.56} \times 100 \% \approx 3.57 \%(\mathrm{B})$
$\Rightarrow \frac{\Delta \mathrm{r}}{\mathrm{r}} \times 100 \%=\frac{1}{10} \times 100=10 \%$
also $\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\Delta \mathrm{R}+\Delta \mathrm{r}}{\mathrm{R}-\mathrm{r}}+\frac{2 \Delta \mathrm{T}}{\mathrm{T}}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}} \times 100 \%=\frac{1+1}{50} \times 100 \%+2(3.57) \%$
$\approx 11 \%(\mathrm{D})$
Avg. absolute error $=\frac{.04+00+.01+.02+.03}{5}=.02$
$\Rightarrow \frac{\Delta \mathrm{T}}{\mathrm{T}} \times 100 \%=\frac{.02}{.56} \times 100 \% \approx 3.57 \%(\mathrm{B})$
$\Rightarrow \frac{\Delta \mathrm{r}}{\mathrm{r}} \times 100 \%=\frac{1}{10} \times 100=10 \%$
also $\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\Delta \mathrm{R}+\Delta \mathrm{r}}{\mathrm{R}-\mathrm{r}}+\frac{2 \Delta \mathrm{T}}{\mathrm{T}}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}} \times 100 \%=\frac{1+1}{50} \times 100 \%+2(3.57) \%$
$\approx 11 \%(\mathrm{D})$
Q. A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is T = 0.01 second and he measures the depth of the well to be L = 20 meters. Take the acceleration due to gravity g = 10 $\mathrm{ms}^{-2}$ and the velocity of sound is 300 $\mathrm{ms}^{-1}$. Then the fractional error in the measurement, $\delta \mathrm{L} / \mathrm{L}$ , is closest to
(A) 0.2 % (B) 5 % (C) 3 % (D) 1 %
[JEE-Advance 2017]
Ans. (D)
Total time taken
$\mathrm{T}=\sqrt{\frac{2\mathrm{L}}{\mathrm{g}}}+\frac{\mathrm{L}}{\mathrm{c}}$
Now, for an error $\delta \mathrm{L}$ in $\mathrm{L}$
We have an error $\delta \mathrm{T}$ in $\mathrm{T}$
So, $\mathrm{T}+\delta \mathrm{T}=\sqrt{\frac{2(\mathrm{L}+\delta \mathrm{L})}{\mathrm{g}}}+\frac{(\mathrm{L}+\delta \mathrm{L})}{\mathrm{c}}$
$=\sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}\left(1+\frac{\delta \mathrm{L}}{\mathrm{L}}\right)}+\frac{\mathrm{L}}{\mathrm{c}}\left(1+\frac{\delta \mathrm{L}}{\mathrm{L}}\right)$
since, $\frac{\delta \mathrm{T}}{\mathrm{T}}$ is very small, hence
$\frac{\delta \mathrm{L}}{\mathrm{L}}$ is also small, so taking binomial approximation
$\mathrm{T}+\delta \mathrm{T}=\sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}}\left(1+\frac{1}{2} \frac{\delta \mathrm{L}}{\mathrm{L}}\right)+\frac{\mathrm{L}}{\mathrm{c}}\left(1+\frac{\delta \mathrm{L}}{\mathrm{L}}\right)$
$\mathrm{T}+\delta \mathrm{T}=(\sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}})+\sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}}\left(\frac{1}{2} \frac{\delta \mathrm{L}}{\mathrm{L}}\right)+\left(\frac{\mathrm{L}}{\mathrm{c}}\right)+\frac{\mathrm{L}}{\mathrm{c}}\left(\frac{\delta \mathrm{L}}{\mathrm{L}}\right)$
$=\left(\sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}}+\frac{\mathrm{L}}{\mathrm{c}}\right)+\left(\frac{1}{2} \sqrt{\frac{2 \mathrm{L}}{\mathrm{g}}}+\frac{\mathrm{L}}{\mathrm{c}}\right)\left(\frac{\delta \mathrm{L}}{\mathrm{L}}\right)$
$=\mathrm{T}+\left(\frac{1}{2} \sqrt{\frac{2 \times 20}{10}}+\frac{20}{300}\right) \frac{\delta \mathrm{L}}{\mathrm{L}}$
$\Rightarrow \delta \mathrm{T}=\left(1+\frac{1}{15}\right) \frac{\delta \mathrm{L}}{\mathrm{L}}$
$\Rightarrow \frac{\delta \mathrm{L}}{\mathrm{L}}=\left(\frac{15}{16}\right) \delta \mathrm{T}$
$=\left(\frac{15}{16}\right)\left(\frac{1}{100}\right)$
Q. Consider the ratio $r=\frac{(1-a)}{(1+a)}$ to be determined by measuring a dimensionless quantity a. If the error in the measurement of a is $\Delta \mathrm{a}(\Delta \mathrm{a} / \mathrm{a}<<1)$ , then what is the error r in determining r ?
(A) $\frac{\Delta a}{(1+a)^{2}}$
(B) $\frac{2 \Delta a}{(1+a)^{2}}$
(C) $\frac{2 \Delta a}{\left(1-a^{2}\right)}$
(D) $\frac{2 a \Delta a}{\left(1-a^{2}\right)}$
[JEE-Advance 2018]
Ans. 4
$\mathbf{r}=\left(\frac{1-\mathrm{a}}{1+\mathrm{a}}\right)$
$\frac{\Delta \mathrm{r}}{\mathrm{r}}=\frac{\Delta(1-\mathrm{a})}{(1-\mathrm{a})}+\frac{\Delta(1+\mathrm{a})}{(1+\mathrm{a})}$
$=\frac{\Delta \mathrm{a}}{(1-\mathrm{a})}+\frac{\Delta \mathrm{a}}{(1+\mathrm{a})}$
$=\frac{\Delta \mathrm{a}(1+\mathrm{a}+1-\mathrm{a})}{(1-\mathrm{a})(1+\mathrm{a})}$
$\therefore \Delta \mathrm{r}=\frac{2 \Delta \mathrm{a}}{(1-\mathrm{a})(1+\mathrm{a})} \frac{(1-\mathrm{a})}{(1+\mathrm{a})}=\frac{2 \Delta \mathrm{a}}{(1+\mathrm{a})^{2}}$
Q. In an experiment the initial number of radioactive nuclei is $3000 .$ It is found that $1000 \pm 40$ nuclei decayed in the first $1.0 \mathrm{s}$. For $|x|<<1, \ln (1+\mathrm{x})=\mathrm{x}$ up to first power in $\mathrm{x} .$ The erron $\Delta \lambda,$ in the determination of the decay constant $\lambda,$ in $\mathrm{s}^{-1},$ is :-
(A) 0.04 (B) 0.03 (C) 0.02 (D) 0.01
[JEE-Advance 2018]
Ans. (C)
$\mathrm{N}=\mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}$
$\ell \mathrm{nN}=\ell \mathrm{nN}_{0}-\lambda \mathrm{t}$
$\frac{\mathrm{d} \mathrm{N}}{\mathrm{N}}=-\mathrm{d} \lambda \mathrm{t}$
Converting to error,
$\frac{\Delta \mathrm{N}}{\mathrm{N}}=\Delta \lambda \mathrm{t}$
$\therefore \Delta \lambda=\frac{40}{2000 \times \mathrm{L}}=0.02$ (N is number of nuclei left undecayed)
Comments
Aanya
Sept. 22, 2020, 12:59 p.m.
really helpful!! but some solutions are not matching with the given question.