Hey, Do you want to learn about the first law of thermodynamics in physics? If yes. Then you are at the right place.
Then the dQ1 – dW1 = dQ2 – dW2. Difference of heat absorbed by the system dQ and work done by the system dW i.e. dQ – dW does not depends on path in between two definite states of the system.
Both dQ and dW depend on the thermodynamic path taken between two equilibrium states, their difference dQ – dW does not.
So, there is a function (internal energy) of the thermodynamic coordinates (P, V and T) whose final value (Uf) minus its initial value (Ui) equals the change dQ – dW in the process.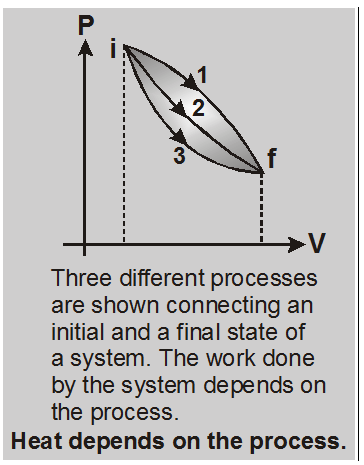
Hence $\mathbf{d} \mathbf{U}=\delta \mathbf{Q}-\delta \mathbf{W}$
This equn. is known as the first law of thermodynamics.
Change in internal energy dU = Uf – Ui does not depends on path it depends only on initial and final positions of the system. So, it is denoted by dU, but heat supplied to the system and work done by the system are path dependent so they are denoted by dQ and dW respectively.
$\delta \mathbf{Q}=\mathrm{d} \mathrm{U}+\delta \mathrm{W}$
Let us consider the melting of a mass m of the solid. Let L be the latent heat of fusion i.e., the heat required to change a unit mass of a solid to liquid phase at constant temperature.
Heat absorbed during melting process, $\delta \mathrm{Q}=\mathrm{mL}$
According to the first law of thermodynamics,
$\delta Q=d U+\delta W$
Or $\mathrm{mL}=\mathrm{dU}$ $[\because \delta W=P \delta V=P \times 0=0]$
So, the internal energy increases by mL during the melting process.
Let us consider the vaporisation of liquid of mass m. Let Vl and Vv be the volume of the liquid and vapours respectively.
Then, the work done in expanding at constant temperature and pressure P,
$\delta W=P \delta V=P\left(V_{v}-V_{\ell}\right)$
Let L be the latent heat of vaporisation, i.e., the heat required to change a unit mass of a liquid to vapour phase at constant temperature and pressure.
\ Heat absorbed during boiling process, dQ = mL
Let Ul and Uv be the internal energies of the liquid and vapours respectively.
Change in internal energy, dU = Uv – Ul
According to the first law of thermodynamics,
$\delta Q=d U+\delta W$
$\therefore \quad \mathrm{mL}=\left(\mathrm{U}_{\mathrm{v}}-\mathrm{U}_{\ell}\right)+\mathrm{P}\left(\mathrm{V}_{\mathrm{v}}-\mathrm{V}_{\ell}\right)$
Or $U_{v}-U_{\ell}=m L-P\left(V_{v}-V_{\ell}\right)$
Knowing all the quantities on right hand side, we can calculate the gain in the internal energy.
For a better understanding of this chapter, please check the detailed notes of the Thermodynamics. If you want more Free Learning Videos and Study Material Then don't forget to download the eSaral App.
The first law of thermodynamics
A gas in a cylinder with a movable piston is a simple example of a thermodynamic system. Let this system changes from an initial equilibrium state i to a final equilibrium state f in a definite way, the heat absorbed by the system being dQ1 and the work done by the system being dW1 and system change its state through path 1, again for path 2 heat absorbed by the system is dQ2 and work done by the system is dW2.Then the dQ1 – dW1 = dQ2 – dW2. Difference of heat absorbed by the system dQ and work done by the system dW i.e. dQ – dW does not depends on path in between two definite states of the system.
Both dQ and dW depend on the thermodynamic path taken between two equilibrium states, their difference dQ – dW does not.
So, there is a function (internal energy) of the thermodynamic coordinates (P, V and T) whose final value (Uf) minus its initial value (Ui) equals the change dQ – dW in the process.
Hence $\mathbf{d} \mathbf{U}=\delta \mathbf{Q}-\delta \mathbf{W}$
This equn. is known as the first law of thermodynamics.
Change in internal energy dU = Uf – Ui does not depends on path it depends only on initial and final positions of the system. So, it is denoted by dU, but heat supplied to the system and work done by the system are path dependent so they are denoted by dQ and dW respectively.
First Law of Thermodynamics:
If some quantity of heat is supplied to a system capable of doing external work, then the quantity of heat absorbed by the system is equal to the sum of the increase in the internal energy of the system and the external work done by the system.$\delta \mathbf{Q}=\mathrm{d} \mathrm{U}+\delta \mathrm{W}$
- [i] The first law of thermodynamics is essentially a restatement of the law of conservation of energy, i.e., energy can neither be created nor be destoryed but may be converted from one form to another.
- [ii] In applying the first law of thermodynamics, all the three quantities, i.e., dQ, dU and dW must be expressed in the same units, i.e., either in units of work or in units of heat.
- [iii] This law is applicable to every process in nature.
- [iv] This law is applicable to all the three phases of matter, i.e., solid, liquid and gas.
- [v] dU may be any type of internal energy-translational kinetic energy, rotational kinetic energy, binding energy etc. It is a characteristic of the state of a system.
- [vi] The first law of thermodynamics introduces the concept of internal energy.
Limitations of First Law of Thermodynamics:
- (a) It does not explain the direction of heat flow.
- (b) It does not explain how much amount of heat given will be converted into work.
Application of first law of thermodynamics in physics
(a) Melting Process :
When a substance melts, the change in volume (dV) is very small and can, therefore, be neglected. The temperature of a substance remains unchanged during melting process.Let us consider the melting of a mass m of the solid. Let L be the latent heat of fusion i.e., the heat required to change a unit mass of a solid to liquid phase at constant temperature.
Heat absorbed during melting process, $\delta \mathrm{Q}=\mathrm{mL}$
According to the first law of thermodynamics,
$\delta Q=d U+\delta W$
Or $\mathrm{mL}=\mathrm{dU}$ $[\because \delta W=P \delta V=P \times 0=0]$
So, the internal energy increases by mL during the melting process.
(b) Boiling Process :
When a liquid is heated, it changes into vapour at constant temperature (called boiling point) and pressure. When water is heated at normal atmospheric pressure, it boils at 100°C. The temperature remains unchanged during the boiling process.Let us consider the vaporisation of liquid of mass m. Let Vl and Vv be the volume of the liquid and vapours respectively.
Then, the work done in expanding at constant temperature and pressure P,
$\delta W=P \delta V=P\left(V_{v}-V_{\ell}\right)$
Let L be the latent heat of vaporisation, i.e., the heat required to change a unit mass of a liquid to vapour phase at constant temperature and pressure.
\ Heat absorbed during boiling process, dQ = mL
Let Ul and Uv be the internal energies of the liquid and vapours respectively.
Change in internal energy, dU = Uv – Ul
According to the first law of thermodynamics,
$\delta Q=d U+\delta W$
$\therefore \quad \mathrm{mL}=\left(\mathrm{U}_{\mathrm{v}}-\mathrm{U}_{\ell}\right)+\mathrm{P}\left(\mathrm{V}_{\mathrm{v}}-\mathrm{V}_{\ell}\right)$
Or $U_{v}-U_{\ell}=m L-P\left(V_{v}-V_{\ell}\right)$
Knowing all the quantities on right hand side, we can calculate the gain in the internal energy.
For a better understanding of this chapter, please check the detailed notes of the Thermodynamics. If you want more Free Learning Videos and Study Material Then don't forget to download the eSaral App.