JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Paragraph for Questions no. 3 to 5
When liquid medicine of density is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
Q. A cylindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200 mm. Find the fall in height (in mm) of water level due to opening of the orifice. [Take atmospheric pressure = $1.0 \times 10^{5} \mathrm{N} / \mathrm{m}^{2},$ density of water $=1000 \mathrm{kg} / \mathrm{m}^{3}$ and g = $10 \mathrm{m} / \mathrm{s}^{2}$ . Neglect any effect of surface tension.]
[IIT-JEE-2009]
Ans. 206
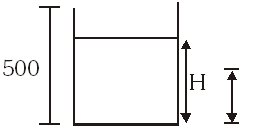 $(500-\mathrm{H}) \mathrm{P}_{0}=300\left(\mathrm{P}_{0}-\mathrm{rg} \times 0.2\right)$
$(0.5-\mathrm{H}) \times 10^{5}=0.3\left[10^{5}-10^{4} \times 0.2\right)$
$0.5-\mathrm{H}=0.294$
H = 206 mm
$(500-\mathrm{H}) \mathrm{P}_{0}=300\left(\mathrm{P}_{0}-\mathrm{rg} \times 0.2\right)$
$(0.5-\mathrm{H}) \times 10^{5}=0.3\left[10^{5}-10^{4} \times 0.2\right)$
$0.5-\mathrm{H}=0.294$
H = 206 mm
 $(500-\mathrm{H}) \mathrm{P}_{0}=300\left(\mathrm{P}_{0}-\mathrm{rg} \times 0.2\right)$
$(0.5-\mathrm{H}) \times 10^{5}=0.3\left[10^{5}-10^{4} \times 0.2\right)$
$0.5-\mathrm{H}=0.294$
H = 206 mm
$(500-\mathrm{H}) \mathrm{P}_{0}=300\left(\mathrm{P}_{0}-\mathrm{rg} \times 0.2\right)$
$(0.5-\mathrm{H}) \times 10^{5}=0.3\left[10^{5}-10^{4} \times 0.2\right)$
$0.5-\mathrm{H}=0.294$
H = 206 mm
Q. Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure $8 \mathrm{N} / \mathrm{m}^{2}$. The radii of bubbles A and B are 2 cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio $\mathrm{n}_{\mathrm{B}} / \mathrm{n}_{\mathrm{A}},$ where $\mathrm{n}_{\mathrm{A}}$ and $\mathrm{n}_{\mathrm{B}}$ are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of grav
[IIT-JEE-2009]
Ans. 6
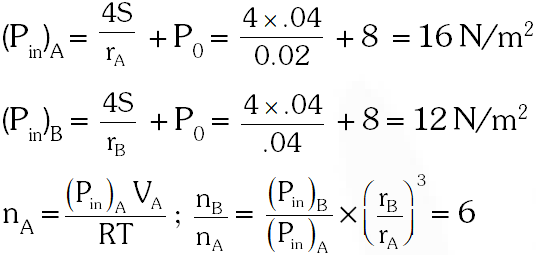
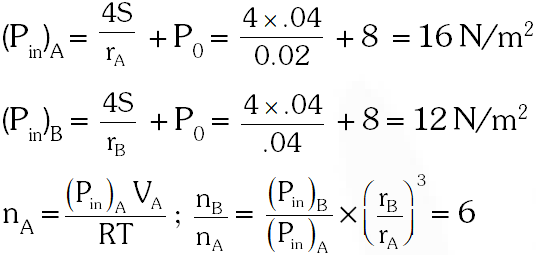
Q. If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius R (assuming r < [IIT-JEE-2010]
Ans. (C)
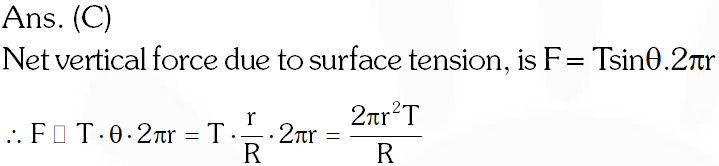
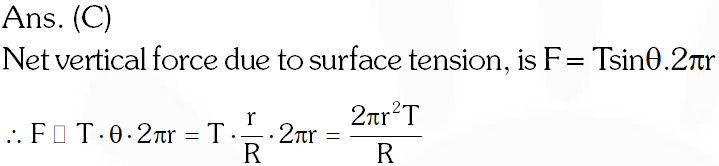
Q. If $\mathrm{r}=5 \times 10^{-4} \mathrm{m}, \rho=10^{3} \mathrm{kgm}^{-3}, \mathrm{g}=10 \mathrm{ms}^{-2}, \mathrm{T}=0.11 \mathrm{Nm}^{-1}$, the radius of the drop when it detaches from the dropper is approximately
(A) $1.4 \times 10^{-3} \mathrm{m}$
(B) $3.3 \times 10^{-3} \mathrm{m}$
(C) $2.0 \times 10^{-3} \mathrm{m}$
(D) $4.1 \times 10^{-3} \mathrm{m}$
[IIT-JEE-2010]
Ans. (A)
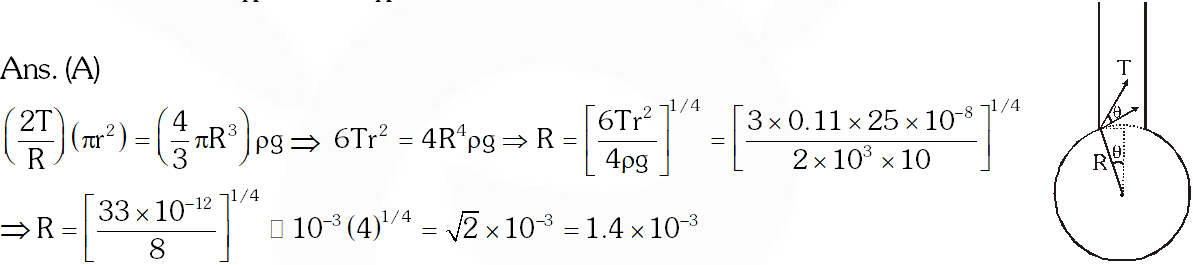
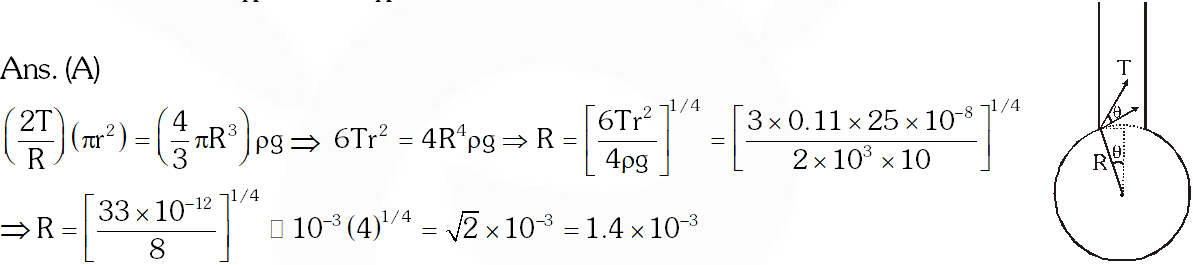
Q. After the drop detaches, its surface energy is
(A) $1.4 \times 10^{-6} \mathrm{J}$
(B) $2.7 \times 10^{-6} \mathrm{J}$
(C) $5.4 \times 10^{-6} \mathrm{J}$
(D) $8.1 \times 10^{-6} \mathrm{J}$
[IIT-JEE-2010]
Ans. (B)
Ans. (B)
$\mathrm{U}=\mathrm{T}\left(4 \pi \mathrm{R}^{2}\right)=0.11 \times 4 \times \pi\left(\sqrt{2} \times 10^{-3}\right)^{2}=2.7 \times 10^{-6} \mathrm{J}$
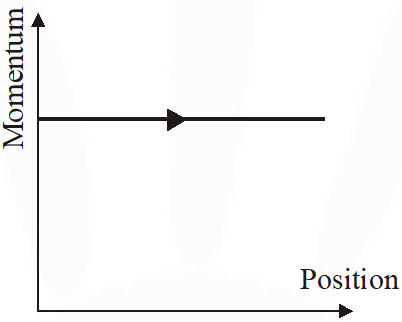
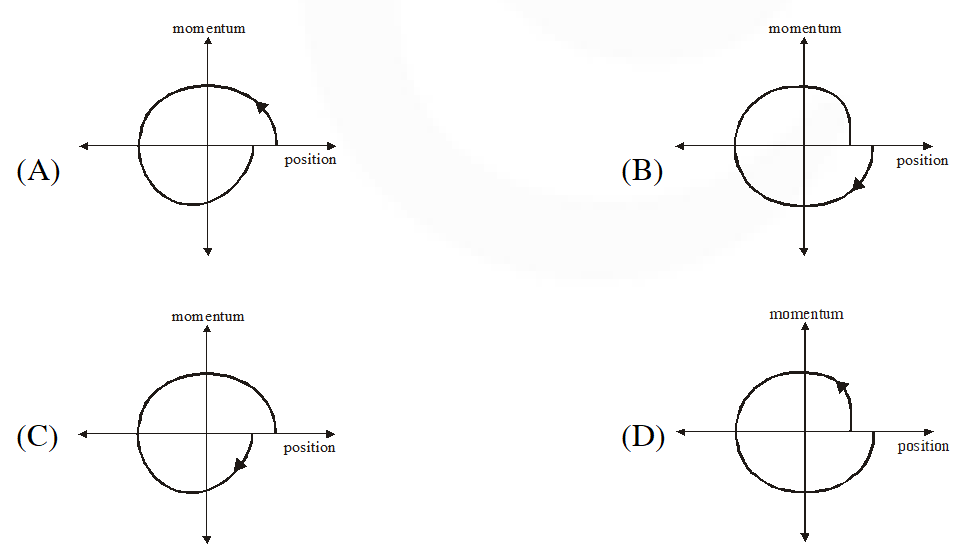
Q. The phase space diagram for a ball thrown vertically up from ground is
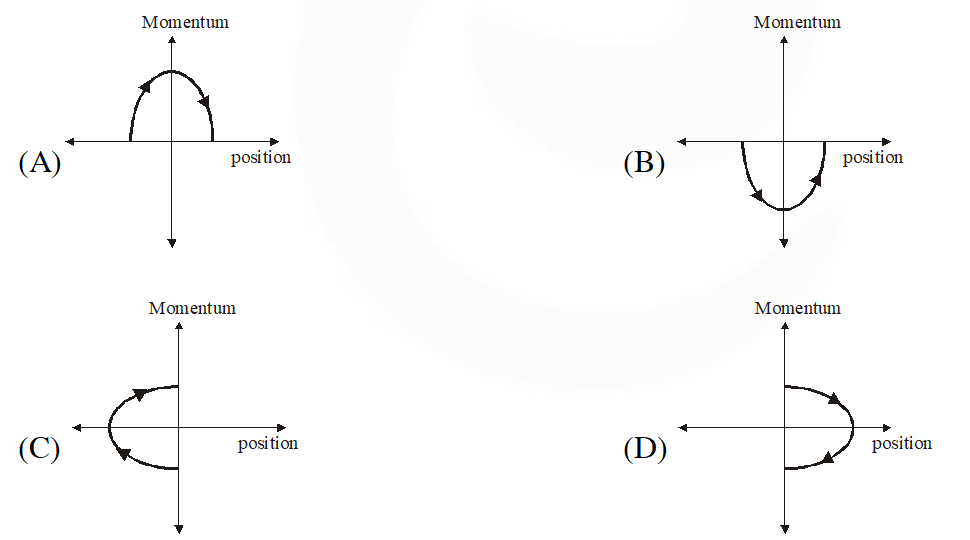 [IIT-JEE-2011]
[IIT-JEE-2011]
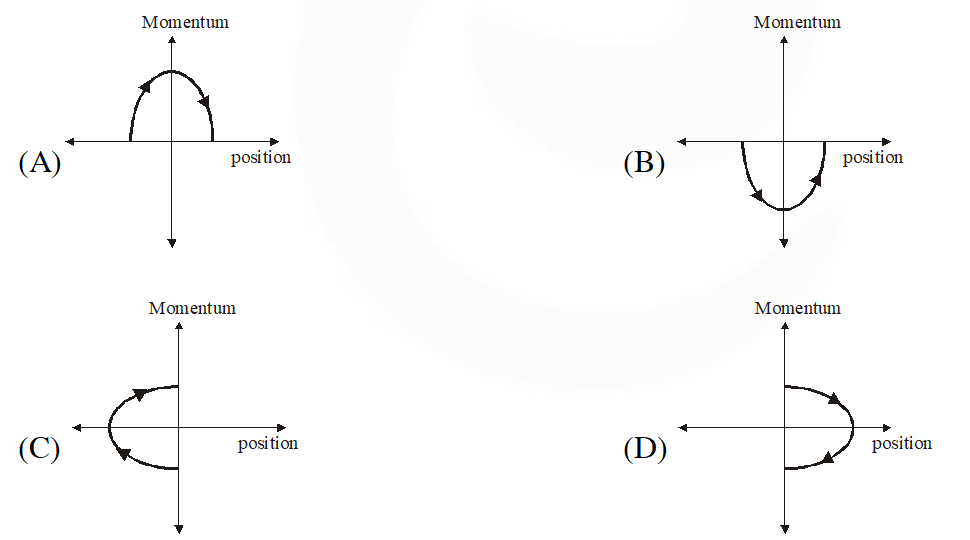 [IIT-JEE-2011]
[IIT-JEE-2011]
Ans. (D)
Initially position increases while momentum decreases

Q. The phase space diagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and $\mathrm{E}_{1}$ and $\mathrm{E}_{2}$ are the total mechanical energies respectively. Then
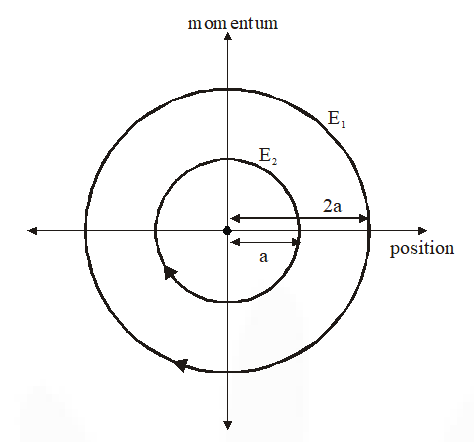 (A) $\mathrm{E}_{1}=\sqrt{2 \mathrm{E}}_{2}$
(B) $\mathrm{E}_{1}=2 \mathrm{E}_{2}$
(C) $\mathrm{E}_{1}=4 \mathrm{E}_{2}$
(D) $\mathrm{E}_{1}=16 \mathrm{E}_{2}$
[IIT-JEE-2011]
(A) $\mathrm{E}_{1}=\sqrt{2 \mathrm{E}}_{2}$
(B) $\mathrm{E}_{1}=2 \mathrm{E}_{2}$
(C) $\mathrm{E}_{1}=4 \mathrm{E}_{2}$
(D) $\mathrm{E}_{1}=16 \mathrm{E}_{2}$
[IIT-JEE-2011]
 (A) $\mathrm{E}_{1}=\sqrt{2 \mathrm{E}}_{2}$
(B) $\mathrm{E}_{1}=2 \mathrm{E}_{2}$
(C) $\mathrm{E}_{1}=4 \mathrm{E}_{2}$
(D) $\mathrm{E}_{1}=16 \mathrm{E}_{2}$
[IIT-JEE-2011]
(A) $\mathrm{E}_{1}=\sqrt{2 \mathrm{E}}_{2}$
(B) $\mathrm{E}_{1}=2 \mathrm{E}_{2}$
(C) $\mathrm{E}_{1}=4 \mathrm{E}_{2}$
(D) $\mathrm{E}_{1}=16 \mathrm{E}_{2}$
[IIT-JEE-2011]
Ans. (C)
$\Rightarrow \mathrm{E}_{1}=\frac{1}{2} \cdot \mathrm{k}(2 \mathrm{a})^{2}=4 \cdot \frac{1}{2} \mathrm{ka}^{2}=4 \mathrm{E}_{2}$
Q. Consider the spring-mass system, with the mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is
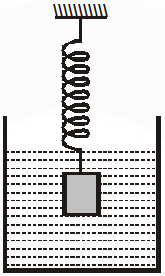
 [IIT-JEE-2011]
[IIT-JEE-2011]

 [IIT-JEE-2011]
[IIT-JEE-2011]
Ans. (B)
Initially position decreases while momentum (–ve) increases and on completion of cycle net KE i.e. is decreased
Q. Two solid spheres A and B of equal volumes but of different densities dA and dB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
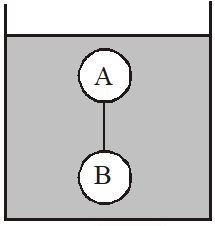 $(\mathrm{A}) \mathrm{d}_{\mathrm{A}}<\mathrm{d}_{\mathrm{F}}$
(B) $\mathrm{d}_{\mathrm{B}}>\mathrm{d}_{\mathrm{F}}$
(C) $\mathrm{d}_{\mathrm{A}}>\mathrm{d}_{\mathrm{F}}$
(D) $\mathrm{d}_{\mathrm{A}}+\mathrm{d}_{\mathrm{B}}=2 \mathrm{d}_{\mathrm{F}}$
[IIT-JEE-2011]
$(\mathrm{A}) \mathrm{d}_{\mathrm{A}}<\mathrm{d}_{\mathrm{F}}$
(B) $\mathrm{d}_{\mathrm{B}}>\mathrm{d}_{\mathrm{F}}$
(C) $\mathrm{d}_{\mathrm{A}}>\mathrm{d}_{\mathrm{F}}$
(D) $\mathrm{d}_{\mathrm{A}}+\mathrm{d}_{\mathrm{B}}=2 \mathrm{d}_{\mathrm{F}}$
[IIT-JEE-2011]
 $(\mathrm{A}) \mathrm{d}_{\mathrm{A}}<\mathrm{d}_{\mathrm{F}}$
(B) $\mathrm{d}_{\mathrm{B}}>\mathrm{d}_{\mathrm{F}}$
(C) $\mathrm{d}_{\mathrm{A}}>\mathrm{d}_{\mathrm{F}}$
(D) $\mathrm{d}_{\mathrm{A}}+\mathrm{d}_{\mathrm{B}}=2 \mathrm{d}_{\mathrm{F}}$
[IIT-JEE-2011]
$(\mathrm{A}) \mathrm{d}_{\mathrm{A}}<\mathrm{d}_{\mathrm{F}}$
(B) $\mathrm{d}_{\mathrm{B}}>\mathrm{d}_{\mathrm{F}}$
(C) $\mathrm{d}_{\mathrm{A}}>\mathrm{d}_{\mathrm{F}}$
(D) $\mathrm{d}_{\mathrm{A}}+\mathrm{d}_{\mathrm{B}}=2 \mathrm{d}_{\mathrm{F}}$
[IIT-JEE-2011]
Ans. (A,B,D)
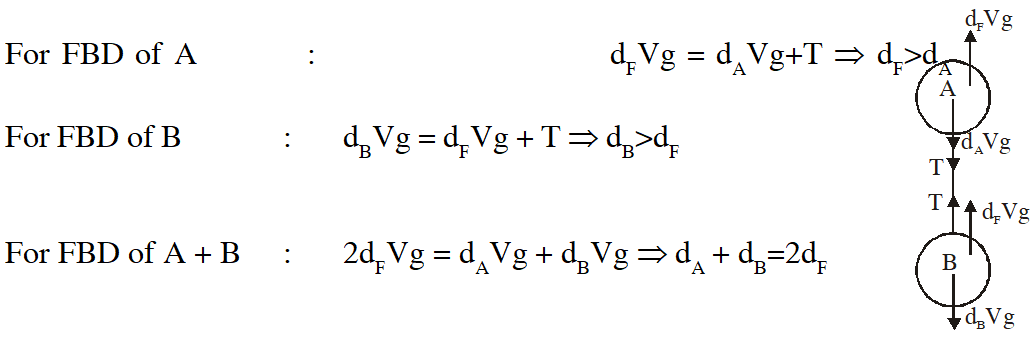
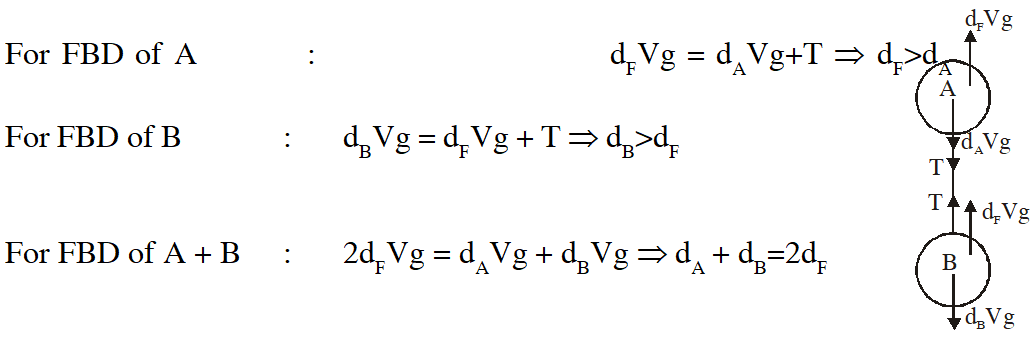
Q. A thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If $\rho_{\mathrm{C}}$ is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is
(A) more than half-filled if $\rho_{\mathrm{c}}$ is less than 0.5
(B) more than half-filled if $\rho_{\mathrm{c}}$ is more than 1.0
(C) half-filled if $\rho_{\mathrm{C}}$ is more than 0.5
(D) less than half-filled if $\rho_{\mathrm{C}}$ is less than 0.5
[IIT-JEE-2012]
Ans. (A)


Q. A solid sphere of radius R and density is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3. The complete arrangement is placed in a liquid of density 2 and is allowed to reach equilibrium. The correct statement(s) is (are)
(A) the net elongation of the spring is $\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
(B) the net elongation of the spring is $\frac{8 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
(C) the light sphere is partially submerged.
(D) the light sphere is completely submerged.
[IIT-JEE-2013]
Ans. (A,D)
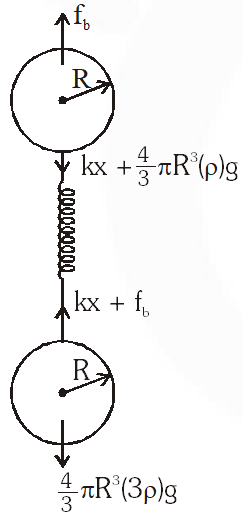 For system
At equilibrium $2 f_{b}=\frac{4}{3} \pi R^{3} \rho g+\frac{4}{3} \pi R^{3}(3 \rho) g$
$2 \mathrm{f}_{\mathrm{b}}=\frac{16}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}=2 \rho\left(\mathrm{v}_{\text {submerged }}\right) \mathrm{g}$
$\Rightarrow \mathrm{v}_{\text {submerged }}=\frac{8}{3} \pi \mathrm{R}^{3}$
$\Rightarrow$ light sphere is completely submerged
Also for one sphere
$\frac{4}{3} \pi \mathrm{R}^{3}(2 \rho) \mathrm{g}=\mathrm{kx}+\frac{4}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}$
$\Rightarrow \mathrm{x}=\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
For system
At equilibrium $2 f_{b}=\frac{4}{3} \pi R^{3} \rho g+\frac{4}{3} \pi R^{3}(3 \rho) g$
$2 \mathrm{f}_{\mathrm{b}}=\frac{16}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}=2 \rho\left(\mathrm{v}_{\text {submerged }}\right) \mathrm{g}$
$\Rightarrow \mathrm{v}_{\text {submerged }}=\frac{8}{3} \pi \mathrm{R}^{3}$
$\Rightarrow$ light sphere is completely submerged
Also for one sphere
$\frac{4}{3} \pi \mathrm{R}^{3}(2 \rho) \mathrm{g}=\mathrm{kx}+\frac{4}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}$
$\Rightarrow \mathrm{x}=\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
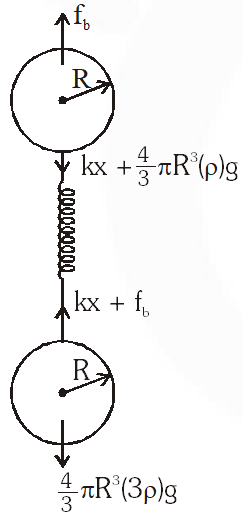 For system
At equilibrium $2 f_{b}=\frac{4}{3} \pi R^{3} \rho g+\frac{4}{3} \pi R^{3}(3 \rho) g$
$2 \mathrm{f}_{\mathrm{b}}=\frac{16}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}=2 \rho\left(\mathrm{v}_{\text {submerged }}\right) \mathrm{g}$
$\Rightarrow \mathrm{v}_{\text {submerged }}=\frac{8}{3} \pi \mathrm{R}^{3}$
$\Rightarrow$ light sphere is completely submerged
Also for one sphere
$\frac{4}{3} \pi \mathrm{R}^{3}(2 \rho) \mathrm{g}=\mathrm{kx}+\frac{4}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}$
$\Rightarrow \mathrm{x}=\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
For system
At equilibrium $2 f_{b}=\frac{4}{3} \pi R^{3} \rho g+\frac{4}{3} \pi R^{3}(3 \rho) g$
$2 \mathrm{f}_{\mathrm{b}}=\frac{16}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}=2 \rho\left(\mathrm{v}_{\text {submerged }}\right) \mathrm{g}$
$\Rightarrow \mathrm{v}_{\text {submerged }}=\frac{8}{3} \pi \mathrm{R}^{3}$
$\Rightarrow$ light sphere is completely submerged
Also for one sphere
$\frac{4}{3} \pi \mathrm{R}^{3}(2 \rho) \mathrm{g}=\mathrm{kx}+\frac{4}{3} \pi \mathrm{R}^{3} \rho \mathrm{g}$
$\Rightarrow \mathrm{x}=\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3 \mathrm{k}}$
Q. A glass capillary tube is of the shape of truncated cone with an apex angle so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to height h, where the radius of its cross section is b. If the surface tension of water is S, its density is , and its contact angle with glass is $\theta$, the value of h will be (g is the acceleration due to gravity)
 [JEE Advanced-2014]
[JEE Advanced-2014]
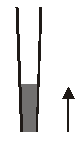 [JEE Advanced-2014]
[JEE Advanced-2014]
Ans. (D)
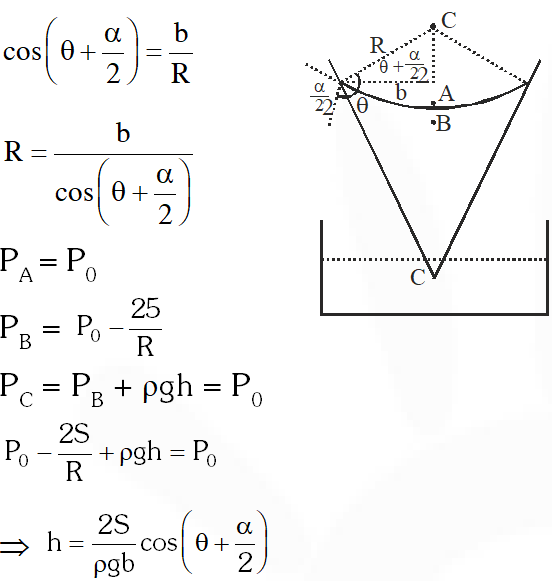

Q. If the piston is pushed at a speed of 5 $\mathrm{mms}^{-1}$, the air comes out of the nozzle with a speed of
(A) $0.1 \mathrm{ms}^{-1}$
(B) $1 \mathrm{ms}^{-1}$
(C) $2 \mathrm{ms}^{-1}$
(D) $8 \mathrm{ms}^{-1}$
[JEE Advanced-2014]
Ans. (C)
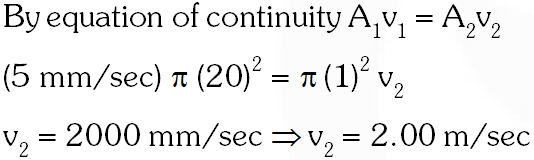
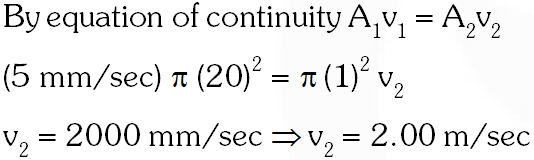
Q. If the density of air is $\rho_{\mathrm{a}}$ and that of the liquid $\rho_{\ell}$, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
(A) $\sqrt{\frac{\rho_{\mathrm{a}}}{\rho_{\ell}}}$
(B) $\sqrt{\rho_{\mathrm{a}} \rho_{\ell}}$
(C) $\sqrt{\frac{p_{6}}{\rho_{0}}}$
$(\mathrm{D}) \rho \ell$
[JEE Advanced-2014]
Ans. (A)
By applying conservation of energy
$\frac{1}{2} \rho_{\mathrm{A}} \mathrm{v}^{2}=\frac{1}{2} \rho_{\mathrm{L}} \mathrm{v}^{2}+\rho_{\mathrm{L}} \mathrm{gH}$
Assuming height of liquid is negligible v $\propto \sqrt{\frac{\rho_{A}}{\rho_{\mathrm{L}}}}$
Q. A person in a lift is holding a water jar, which has a small hole at the lower end of its side. When the lift is at rest, the water jet coming out of the hole hits the floor of the lift at a distance d of 1.2 m from the person. In the following, state of the lift's motion is given in List I and the distance where the water jet hits the floor of the lift is given in List II. Match the statements from List I with those in List II and select the correct answer using the code given below the lists.
 [JEE Advanced-2014]
[JEE Advanced-2014]
 [JEE Advanced-2014]
[JEE Advanced-2014]
Ans. (C)
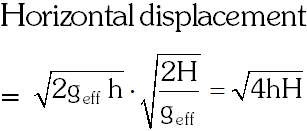
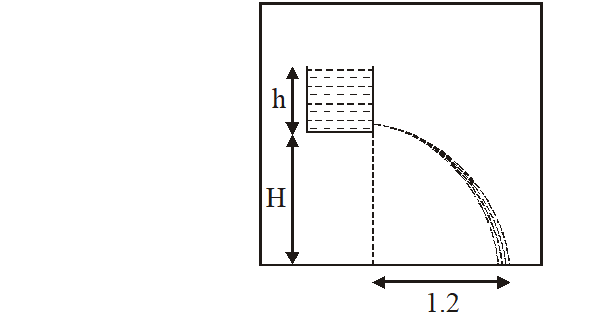 Since $\mathrm{g}_{\mathrm{eff}}$ cancelled out therefore distance will be same in case P, Q and R. When lift falls freely no water leaks out of Jar.
Since $\mathrm{g}_{\mathrm{eff}}$ cancelled out therefore distance will be same in case P, Q and R. When lift falls freely no water leaks out of Jar.
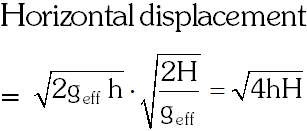
 Since $\mathrm{g}_{\mathrm{eff}}$ cancelled out therefore distance will be same in case P, Q and R. When lift falls freely no water leaks out of Jar.
Since $\mathrm{g}_{\mathrm{eff}}$ cancelled out therefore distance will be same in case P, Q and R. When lift falls freely no water leaks out of Jar.
Q. Two spheres P and Q of equal radii have densities $\rho_{1}$ and $\rho_{2}$, respectively. The spheres are connected by a massless string and placed in liquids $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ of densities $\sigma_{1}$ and $\sigma_{2}$ and viscosities $\eta_{1}$ and $\eta_{2}$, respectively. They float in equilibrium with the sphere P in $\mathbf{L}_{1}$ and sphere Q in $\mathrm{L}_{2}$ and the string being taut (see figure). If sphere P alone in $\mathrm{L}_{2}$ has terminal velocity and Q alone in $\mathrm{L}_{1}$ has terminal velocity , then
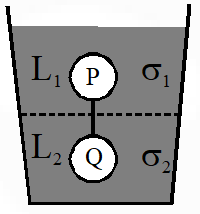
 [JEE Advanced-2015]
[JEE Advanced-2015]

 [JEE Advanced-2015]
[JEE Advanced-2015]
Ans. (A,D)
Consider a body of density $\mathrm{P}_{\mathrm{b}}$ kept in density $P_{\ell}$ whose viscosity is $\eta$ and terminal velocity V. Then
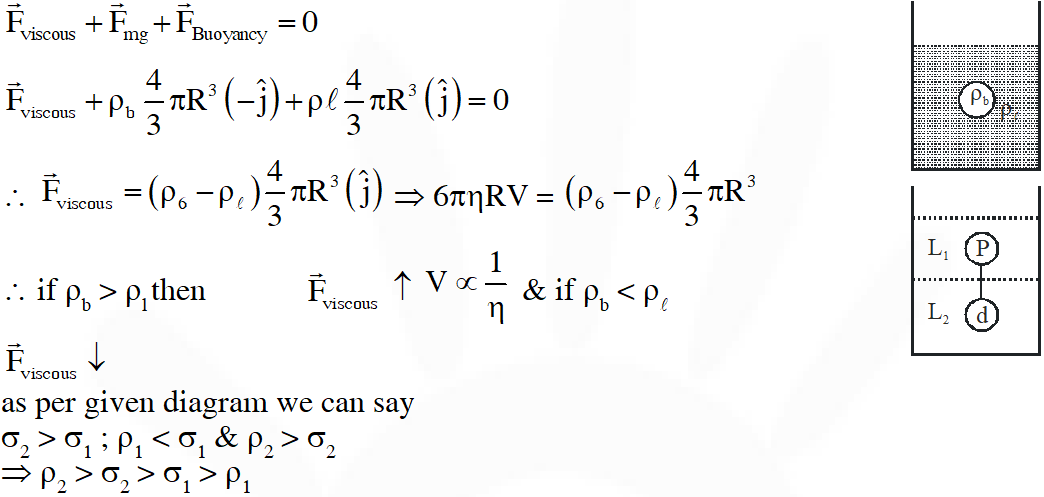
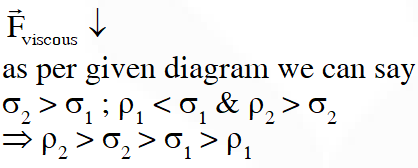
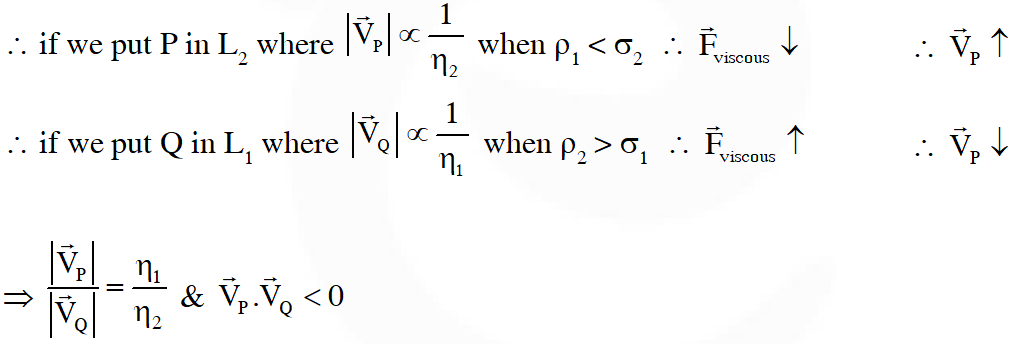
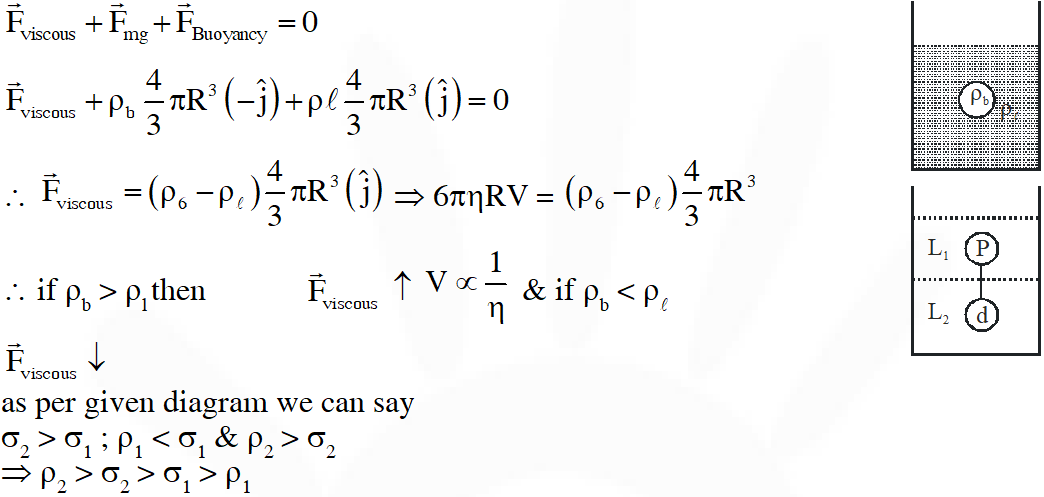
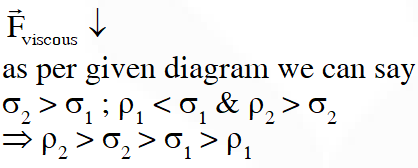
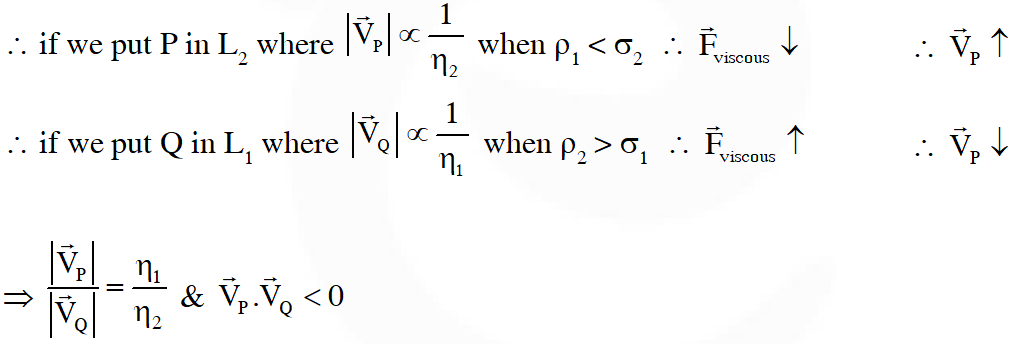
Q. Consider two solid spheres P and Q each of density 8 gm $\mathrm{cm}^{-3}$ and diameters 1 cm and 0.5 cm, respectively. Sphere P is dropped into a liquid of density 0.8 gm $\mathrm{cm}^{-3}$ and viscosity $\eta=3$ poiseulles. Sphere Q is dropped into a liquid of density 1.6 gm $\mathrm{cm}^{-3}$ and viscosity $\eta=2$poiseulles. The ratio of the terminal velocities of P and Q is
[JEE Advanced-2016]
Ans. 3
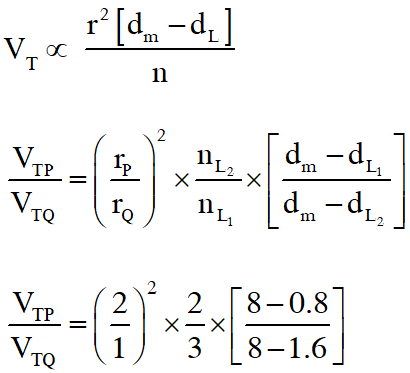 $\frac{V_{\mathrm{TP}}}{V_{\mathrm{TQ}}}=3$
$\frac{V_{\mathrm{TP}}}{V_{\mathrm{TQ}}}=3$
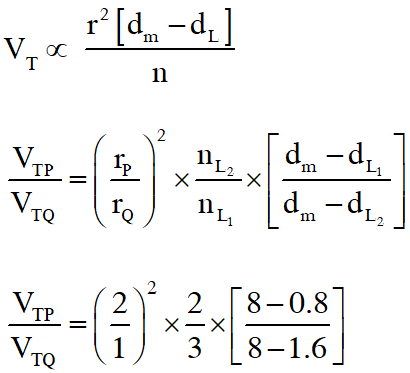 $\frac{V_{\mathrm{TP}}}{V_{\mathrm{TQ}}}=3$
$\frac{V_{\mathrm{TP}}}{V_{\mathrm{TQ}}}=3$
Q. A drop of liquid of radius R = $10^{-2}$ m having surface tension S = $=\frac{0.1}{4 \pi} \mathrm{Nm}^{-1}$ divides itself into K identical drops. In this process the total change in the surface energy $\Delta \mathrm{U}=10^{-3} \mathrm{J} .$ If $\mathrm{K}=10^{\alpha}$ then the value of is
[JEE Advanced-2017]
Ans. 6
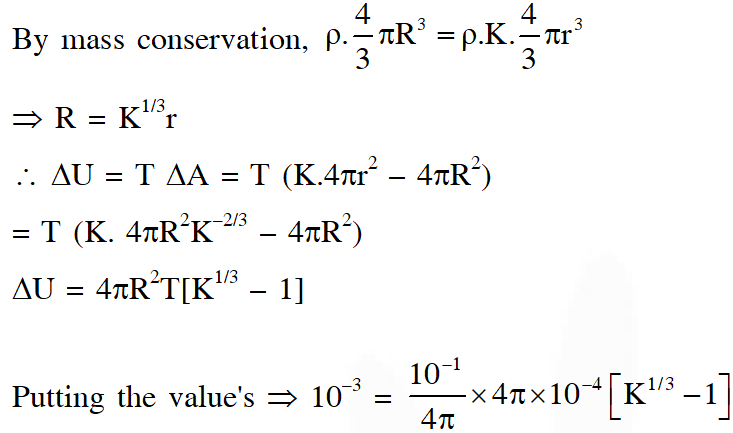
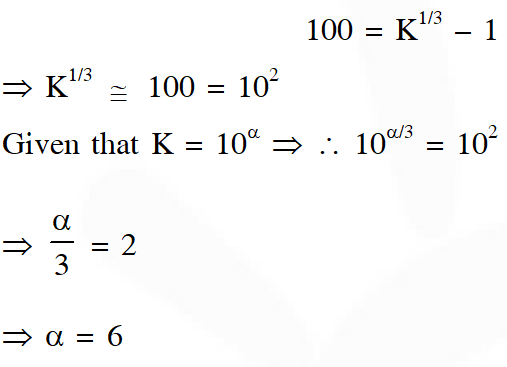
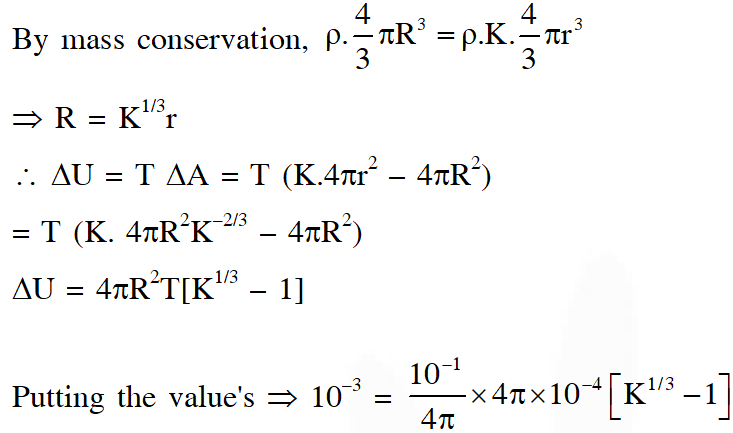
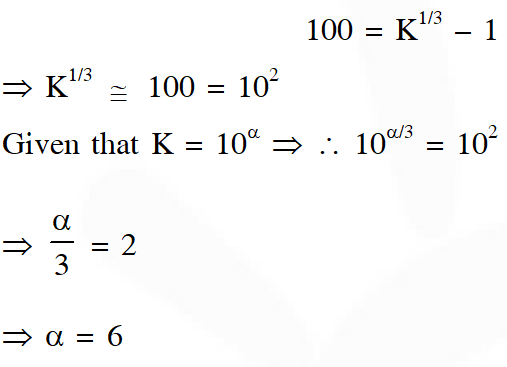
Q. A uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is $\sigma$. The angle of contact between water and the wall of the capillary tube is $\theta$. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
(A) For a given material of the capillary tube, h decreases with increase in r
(B) For a given material of the capillary tube, h is independent of $\sigma$.
(C) If this experiment is performed in a lift going up with a constant acceleration, then h decreases.,
(D) h is proportional to contact angle $\theta$.
[JEE Advanced-2017]
Ans. (A,C)
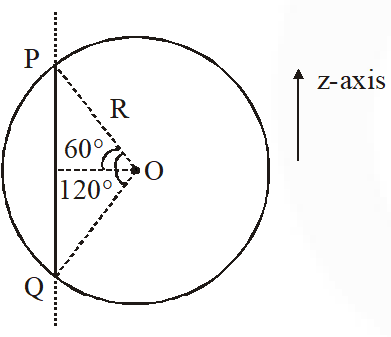 Field due to straight wire is perpendicular to the wire & radially outward. Hence $\mathrm{E}_{z}=0$ Length, $\mathrm{PQ}=2 \mathrm{R} \sin 60=\sqrt{3} \mathrm{R}$According to Gauss's law
total flux $=\left[\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}_{\mathrm{in}}}{\epsilon_{0}}=\frac{\lambda \sqrt{3} \mathrm{R}}{\epsilon_{0}}\right.$
Field due to straight wire is perpendicular to the wire & radially outward. Hence $\mathrm{E}_{z}=0$ Length, $\mathrm{PQ}=2 \mathrm{R} \sin 60=\sqrt{3} \mathrm{R}$According to Gauss's law
total flux $=\left[\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}_{\mathrm{in}}}{\epsilon_{0}}=\frac{\lambda \sqrt{3} \mathrm{R}}{\epsilon_{0}}\right.$
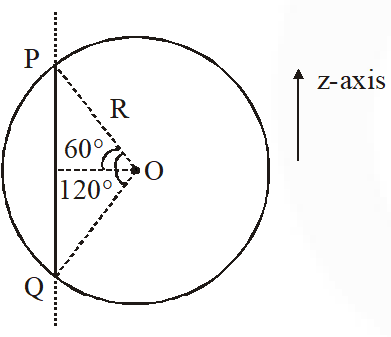 Field due to straight wire is perpendicular to the wire & radially outward. Hence $\mathrm{E}_{z}=0$ Length, $\mathrm{PQ}=2 \mathrm{R} \sin 60=\sqrt{3} \mathrm{R}$According to Gauss's law
total flux $=\left[\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}_{\mathrm{in}}}{\epsilon_{0}}=\frac{\lambda \sqrt{3} \mathrm{R}}{\epsilon_{0}}\right.$
Field due to straight wire is perpendicular to the wire & radially outward. Hence $\mathrm{E}_{z}=0$ Length, $\mathrm{PQ}=2 \mathrm{R} \sin 60=\sqrt{3} \mathrm{R}$According to Gauss's law
total flux $=\left[\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}_{\mathrm{in}}}{\epsilon_{0}}=\frac{\lambda \sqrt{3} \mathrm{R}}{\epsilon_{0}}\right.$
Q. Consider a thin square plate floating on a viscous liquid in a large tank. The height h of the liquid in the tank is much less than the width of the tank. The floating plate is pulled horizontally with a constant velocity $\mathrm{u}_{0}$. Which of the following statements is (are) true ?
(A) The resistive force of liquid on the plate is inversely proportional to h
(B) The resistive force of liquid on the plate is independent of the area of the plate
(C) The tangential (shear) stress on the floor of the tank increases with $\mathrm{u}_{0}$.
(D) The tangential (shear) stress on the plate varies linearly with the viscosity $\eta$ of the liquid.
[JEE Advanced-2018]
Ans. (A,C,D)
 Viscous force is given by F = $-\eta \mathrm{A} \frac{\mathrm{dv}}{\mathrm{dy}}$ since h is very small therefore, magnitude of viscous force is given by
$\mathrm{F}=\eta \mathrm{A} \frac{\Delta \mathrm{v}}{\Delta \mathrm{y}}$
$\therefore \mathrm{F}=\frac{\eta \mathrm{Au}_{0}}{\mathrm{h}} \Rightarrow \mathrm{F} \propto \eta \& \mathrm{F} \propto \mathrm{u}_{0} \quad ; \quad \mathrm{F} \propto \frac{1}{\mathrm{h}}, \mathrm{F} \propto \mathrm{A}$
Since plate is moving with constant velocity, same force must be acting on the floor.
Viscous force is given by F = $-\eta \mathrm{A} \frac{\mathrm{dv}}{\mathrm{dy}}$ since h is very small therefore, magnitude of viscous force is given by
$\mathrm{F}=\eta \mathrm{A} \frac{\Delta \mathrm{v}}{\Delta \mathrm{y}}$
$\therefore \mathrm{F}=\frac{\eta \mathrm{Au}_{0}}{\mathrm{h}} \Rightarrow \mathrm{F} \propto \eta \& \mathrm{F} \propto \mathrm{u}_{0} \quad ; \quad \mathrm{F} \propto \frac{1}{\mathrm{h}}, \mathrm{F} \propto \mathrm{A}$
Since plate is moving with constant velocity, same force must be acting on the floor.
Comments
ESARAL KA BAP
Aug. 23, 2022, 7:08 p.m.
Hud hud dabang dabang kyu hota hai hud hud badang badang kyo nahi?
