Formulas on Time and Work with Example and Tips

Formulas on time and work are easy math equations that help you solve problems about how long a task takes to finish. To understand them, you need to know about time, work, and rate. Simple formulas help you find how long a task takes or how much work is done when you know the rate. Compound formulas help you find how much work is done by more than one person or machine working together, how much work is done when they work one after the other, or how efficient a person or machine is. Knowing these formulas can help 8th grade students make quick and accurate calculations and solve everyday problems.

Downlod Time and work Formula PDF with Short Tricks

Table of content

• Important formulas on time and work

• Time and work Efficiency Formula

• Tips to remember the Formulas on time and work (time and work short tricks)

• Examples on Formulas on Time and Work 

• Types of problems that can be made on time and work

• FAqs

Important formulas on time and work:

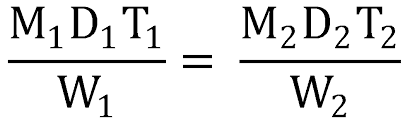
1. Formula for finding time: Time = Work / Rate

2. Formula for finding work: Work = Rate x Time

3. Formula for finding rate: Rate = Work / Time

Time and Work Efficiency Formula

1. Formula for finding work done by a person or machine: Work = Efficiency x Time

2. Formula for finding work done by two or more persons or machines working together: Work = (Efficiency1 + Efficiency2 + ... + EfficiencyN) x Time

3. Formula for finding work done when persons or machines work alternately: Work = Total Work / (Time1 / Efficiency1 + Time2 / Efficiency2 + ... + TimeN / EfficiencyN)

4. Formula for finding the efficiency of a person or machine: Efficiency = Work / (Time x 100%)

Note that these formulas assume that work is done at a constant rate. In real-world scenarios, work rate may vary over time. Also, these formulas may have different units of measurement for time, work, and rate, depending on the context of the problem.

Time, Work, Rate, and Efficiency are key terms used in problems related to time and work. Here's a brief explanation of each term:

1. Time: Time refers to the amount of time it takes to complete a task. It is usually measured in hours, days, or minutes.

2. Work: Work refers to the amount of work required to complete a task. It is usually measured in units of work, such as meters, liters, or items produced.

3. Rate: Rate refers to the amount of work done per unit of time. It is usually measured in units of work per hour, per day, or per minute.

4. Efficiency: Efficiency refers to the ability to perform work with minimal waste or effort. In problems related to time and work, efficiency is usually expressed as a percentage, such as 80% or 90%. It represents the portion of work that is completed relative to the amount of effort put in.

Understanding these terms and how they relate to one another is crucial in solving problems related to time and work. For example, the formula for calculating work is W = F x D, where W is work, F is the force applied, and D is the distance traveled. The formula for calculating rate is R = W / T, where R is rate, W is work, and T is time. And the formula for calculating efficiency is E = (W / (F x D)) x 100%, where E is efficiency, W is work, F is force, and D is distance.

Also read, Difference between discovery and invention

Tips to remember the Formulas on time and work (time and work short tricks)

Here are some tips to remember the formulas on time and work:

1. Understand the concepts: Instead of just memorizing formulas, it is important to understand the underlying concepts and how they relate to real-world situations. This can help you remember the formulas more easily.

2. Practice regularly: The more you practice solving problems related to time and work, the more familiar you will become with the formulas. Regular practice can help you remember the formulas better.

3. Use mnemonics: Mnemonics are memory aids that can help you remember the formulas more easily. For example, you can use the phrase "Wet Rag" to remember the formula for work: W = F x D.

4. Write down the formulas: Writing down the formulas can help you commit them to memory more easily. You can create flashcards with the formulas and practice reciting them.

5. Understand the units of measurement: It is important to understand the units of measurement used in time and work problems, such as hours, minutes, days, and units of work. This can help you apply the formulas correctly and avoid errors.

6. Break down complex problems: Complex problems can be overwhelming, but breaking them down into smaller parts can make them easier to solve. Identify the relevant formulas and apply them step by step to arrive at the solution.

7. Seek help if needed: If you are struggling to remember the formulas or solve problems, don't hesitate to seek help from a teacher or tutor. They can provide guidance and support to help you improve your skills.

Examples on Formulas on Time and Work 

Here are few time and work formula with examples:

Example 1

If a machine can complete a task in 8 hours and another machine can complete the same task in 10 hours, how long will it take both machines to complete the task working together?

Solution: Let's use the formula for finding work done by two or more machines working together:

Work = (Efficiency1 + Efficiency2) x Time

Assuming that the work required is 1 unit, we can calculate the efficiency of each machine as follows:

Machine 1 Efficiency = 1 / 8 = 0.125 Machine 2 Efficiency = 1 / 10 = 0.1

Then, we can substitute these values into the formula to find the time taken to complete the work:

1 = (0.125 + 0.1) x Time 1 = 0.225 x Time Time = 4.44 hours (approx.)

Therefore, it will take both machines working together approximately 4.44 hours to complete the task.

Example 2

If it takes 12 workers to complete a task in 10 days, how long will it take 18 workers to complete the same task?

Solution: Let's use the formula for finding time when we know the work and the rate:

Time = Work / Rate

Assuming that the work required is 1 unit, we can calculate the rate of each worker as follows:

Rate per worker = Work / (Time x Number of Workers) Rate per worker = 1 / (10 x 12) = 0.0083

Then, we can substitute the rate per worker and the number of workers into the formula to find the time taken to complete the task:

Time = 1 / (0.0083 x 18) = 7.21 days (approx.)

Therefore, it will take 18 workers approximately 7.21 days to complete the task.

Example 3

If a person can complete a task in 6 days and another person can complete the same task in 9 days, how long will it take both persons to complete the task if they work together for the first 3 days and then one person leaves?

Solution: Let's use the formula for finding work done when persons or machines work alternately:

Work = Total Work / (Time1 / Efficiency1 + Time2 / Efficiency2)

Assuming that the work required is 1 unit, we can calculate the efficiency of each person as follows:

Person 1 Efficiency = 1 / 6 = 0.1667 Person 2 Efficiency = 1 / 9 = 0.1111

Then, we can substitute the efficiency values and the time values into the formula to find the work done in the first 3 days:

Work done in the first 3 days = (1 / 3) x (0.1667 + 0.1111) = 0.0926

After 3 days, only one person is working, so the time taken to complete the remaining work is:

Time = 0.9074 / 0.1667 = 5.44 days (approx.)

Therefore, it will take both persons approximately 8.44 days (3 + 5.44) to complete the task if they work together for the first 3 days and then one person leaves.

Example 4

If a machine can complete a task in 4 hours and its efficiency is 80%, how much work will the machine do in 2 hours?

Solution: Let's use the formula for finding work done by a person or machine:

Work = Efficiency x Time

Assuming that the efficiency is 80%, we can calculate the work done 

as follows:

Efficiency = 80% = 0.8 Time = 2 hours

Then, we can substitute these values into the formula to find the work done by the machine:

Work = 0.8 x 2 = 1.6 units of work

Therefore, the machine will do 1.6 units of work in 2 hours.

Example 5

If it takes 4 men to complete a task in 8 days, how many days will it take 2 men to complete the same task?

Solution: Let's use the formula for finding time when we know the work and the rate:

Time = Work / Rate

Assuming that the work required is 1 unit, we can calculate the rate of each man as follows:

Rate per man = Work / (Time x Number of Men) Rate per man = 1 / (8 x 4) = 0.03125

Then, we can substitute the rate per man and the number of men into the formula to find the time taken to complete the task with 2 men:

Time = 1 / (0.03125 x 2) = 32 days

Therefore, it will take 2 men approximately 32 days to complete the same task that 4 men completed in 8 days.

Types of problems that can be made on time and work

There are several types of problems that can be made on time and work, including:

1. Work done by one person or machine: These problems involve calculating the amount of work done by a person or machine in a given amount of time.

2. Work done by multiple people or machines: These problems involve calculating the amount of work done by multiple people or machines working together or separately.

3. Work that increases or decreases with time: These problems involve calculating the amount of work done when the efficiency of the person or machine changes over time.

4. Work that depends on the number of people or machines: These problems involve calculating the amount of work done when the number of people or machines working on the task changes.

5. Work that involves fractions of a job: These problems involve calculating the amount of work done when the job can only be completed in fractions, such as half or a quarter of the job.

6. Work that involves wages: These problems involve calculating the wages earned by a person for completing a job in a given amount of time.

7. Work that involves different rates: These problems involve calculating the amount of work done when different people or machines have different rates of completing the job.

By practicing these different types of problems, students can develop a deeper understanding of time and work concepts and become better equipped to solve more complex problems.

Looking for a reliable and effective way to prepare for your exams? Look no further than the eSaral app! Our app is the ultimate destination for students who want to excel in their academic pursuits.

With eSaral, you'll get access to a wide range of high-quality study materials and resources, including video lectures, notes, practice quizzes, and more. Whether you're studying for your school exams or preparing for entrance exams like JEE and NEET, our app has everything you need to succeed.

So what are you waiting for? Download the eSaral app today and take your academic success to the next level!

Frequently Asked Questions