JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Q. A block of mass m is on an inclined plane of angle $\theta$. The coefficient of friction between the block and the plane is $\mu$ m and tan$\theta$ >m. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from $P_{1}$ = mg (sin$\theta$ – $\mu \mathrm{cos} \theta$) to $P_{2}$=mg$(\sin \theta+\mu \cos \theta)$, the frictional force f versus P graph will look like
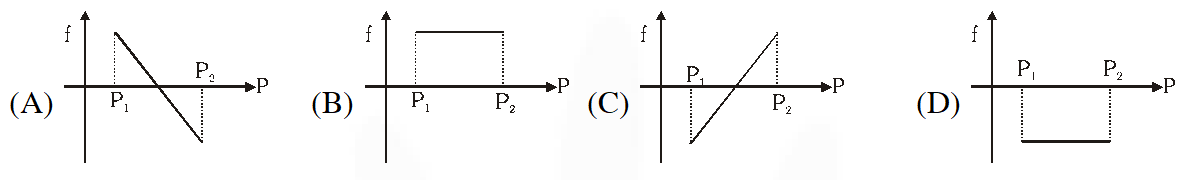[IIT-JEE-2010]
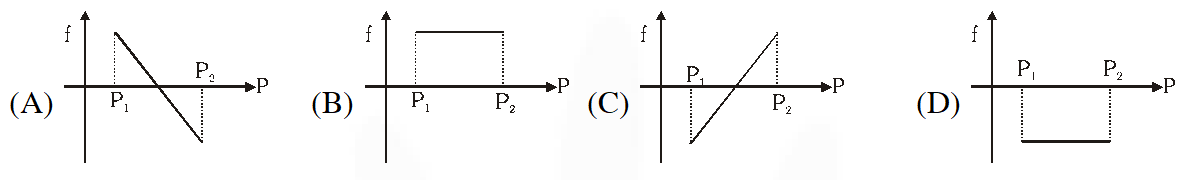[IIT-JEE-2010]
Ans. (A)
Q. A block is moving on an inclined plane making an angle $45^{\circ}$ with the horizontal and the coefficient of friction is $\mu$. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define $\mathrm{N}=10 \mu$, then N is
[IIT-JEE-2011]
Ans. 5
$\mathrm{F}=\operatorname{mg} \sin \theta+\mu \operatorname{mg} \cos \theta$
$\mathrm{F}+\mu \mathrm{mg} \cos \theta=\operatorname{mg} \sin \theta$
$\mathrm{F}=\mathrm{mg} \sin \theta-\mu \mathrm{mg} \cos \theta$
$\operatorname{mg} \sin \theta+\mu \operatorname{mg} \cos \theta=3 \operatorname{mg} \sin \theta-3 \mu \operatorname{mg} \cos \theta$
$4 \mu \mathrm{mg} \cos \theta=2 \mathrm{mg} \sin \mu$
$4 u \cos \theta=2 \sin \theta$
$4 \mu=2 \tan \theta$
$\mathrm{N}=10 \times \frac{1}{2}$
$\mathrm{N}=5 \quad \mu=\frac{1}{2}$
$\mathrm{F}=\operatorname{mg} \sin \theta+\mu \operatorname{mg} \cos \theta$
$\mathrm{F}+\mu \mathrm{mg} \cos \theta=\operatorname{mg} \sin \theta$
$\mathrm{F}=\mathrm{mg} \sin \theta-\mu \mathrm{mg} \cos \theta$
$\operatorname{mg} \sin \theta+\mu \operatorname{mg} \cos \theta=3 \operatorname{mg} \sin \theta-3 \mu \operatorname{mg} \cos \theta$
$4 \mu \mathrm{mg} \cos \theta=2 \mathrm{mg} \sin \mu$
$4 u \cos \theta=2 \sin \theta$
$4 \mu=2 \tan \theta$
$\mathrm{N}=10 \times \frac{1}{2}$
$\mathrm{N}=5 \quad \mu=\frac{1}{2}$
Q. A block of mass $\mathrm{m}_{1}$ = 1 kg another mass $\mathrm{m}_{2}$ = 2kg, are placed together (see figure) on an inclined plane with angle of inclination $\theta$. Various values of $\theta$ are given in List I. The coefficient of friction between the block $\mathrm{m}_{1}$ and the plane is always zero. The coefficient of static and dynamic friction between the block $\mathrm{m}_{2}$ and the plane are equal to $\mu=$ = 0.3. In List II expressions for the friction on block m2 are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g.
[useful information: $\left.\tan \left(5.5^{\circ}\right) \approx 0.1 ; \tan \left(11.5^{\circ}\right) \approx 0.2 ; \tan \left(16.5^{\circ}\right) \approx 0.3\right]$
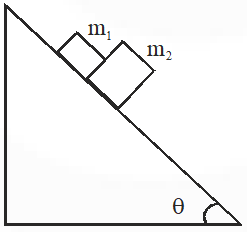
[IIT-JEE-2014]
[IIT-JEE-2014]
Ans. (D)
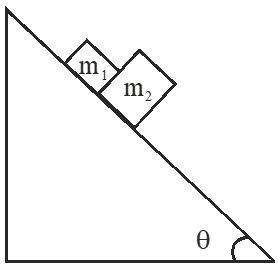The system slip down if
$\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{g} \sin \theta>\mu \mathrm{m}_{2} \mathrm{gcos} \theta$
$\tan \theta>\frac{\mu \mathrm{m}_{2}}{\mathrm{m}_{1}+\mathrm{m}_{2}}>\frac{0.3 \times 2}{3}$
$\tan \theta>0.2$
$\Rightarrow \theta>11.5^{\circ}$
For $\mathrm{P}$ and $\mathrm{Q}$ system will remain stationary hence friction $=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{g} \sin \theta$
For $\mathrm{R}$ and $\mathrm{S}$ system will move hence limiting friction acts friction $=\mu \mathrm{m}_{2} \mathrm{g} \cos \theta$
The system slip down if
$\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{g} \sin \theta>\mu \mathrm{m}_{2} \mathrm{gcos} \theta$
$\tan \theta>\frac{\mu \mathrm{m}_{2}}{\mathrm{m}_{1}+\mathrm{m}_{2}}>\frac{0.3 \times 2}{3}$
$\tan \theta>0.2$
$\Rightarrow \theta>11.5^{\circ}$
For $\mathrm{P}$ and $\mathrm{Q}$ system will remain stationary hence friction $=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{g} \sin \theta$
For $\mathrm{R}$ and $\mathrm{S}$ system will move hence limiting friction acts friction $=\mu \mathrm{m}_{2} \mathrm{g} \cos \theta$
Comments
Bhavya
June 8, 2023, 7:08 p.m.
Arre yhi question Allen ke modules main bhi h chlo match ho skte tha but iss sequence main h question how is it possible
Bhavya
June 8, 2023, 7:08 p.m.
Arre yhi question Allen ke modules main bhi h chlo match ho skte tha but iss sequence main h question how is it possible
Nov. 4, 2020, 10:42 a.m.
these are not hard at all
searching for different type of applications of concept.
Thank You