Hey, do you want to learn about Gauss Law in electrostatics? If yes. Then keep reading.
Gauss law
It relates the total flux of an electric field through a closed surface to the net charge enclosed by that surface. According to it, the total flux linked with a closed surface is $1 / \varepsilon_{0}$ times the charge enclosed by the closed surface,
Mathematically
$\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} s}=\frac{\mathrm{q}}{\varepsilon_{0}}$
Important points
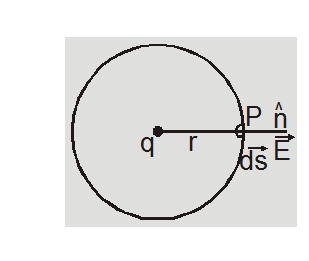
[1] Gauss's law and Coulomb's law are equivalent. If we assume Coulomb's law we can prove Gauss's law and vice versa. To prove Gauss's law from Coulomb's law consider a hypothetical spherical surface called Gaussian surface of radius r with point charge q at its centre. By Coulomb's
law intensity at a point P on the surface will be
$\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{3}} \overrightarrow{\mathrm{r}}$
electric flux linked with area $\overrightarrow{\mathrm{d} s}$
$\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} s}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{3}} \overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{d}}$
direction of $\vec{r}$ and $\overrightarrow{\mathrm{d}} \mathrm{s}$ are same i.e.,
$\vec{r} \cdot \overrightarrow{d s}=r d s \cos 0^{\circ}=r d s$
So,
$\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d}} \mathrm{s}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \mathrm{ds}$
Or
$\oint_{s} \vec{E} \cdot \overrightarrow{d s}$
$=\oint_{s} \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}} d s$
for all points on the sphere r = constant
$\oint \vec{E} \cdot \overrightarrow{d s}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}$
$\oint_{s} d s=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\left(4 \pi r^{2}\right)$
[as $\left.\oint \mathrm{ds}=4 \pi \mathrm{r}^{2}\right]$
$=\frac{q}{\varepsilon_{0}}$
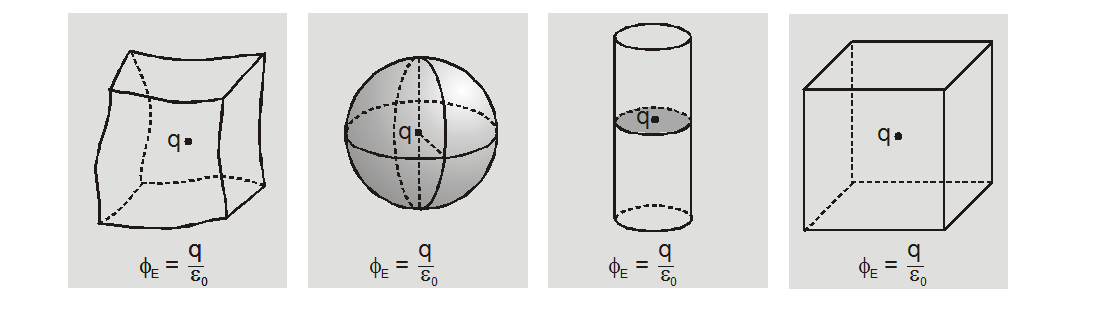
The results are true for any arbitrary surface provided the surface is closed.
[2] It relates the total flux linked with a closed surface to the charge enclosed by the closed surface:
(i) If a closed body not enclosing any charge is placed in either uniform on non-uniform electric field total flux linked with it will be zero.
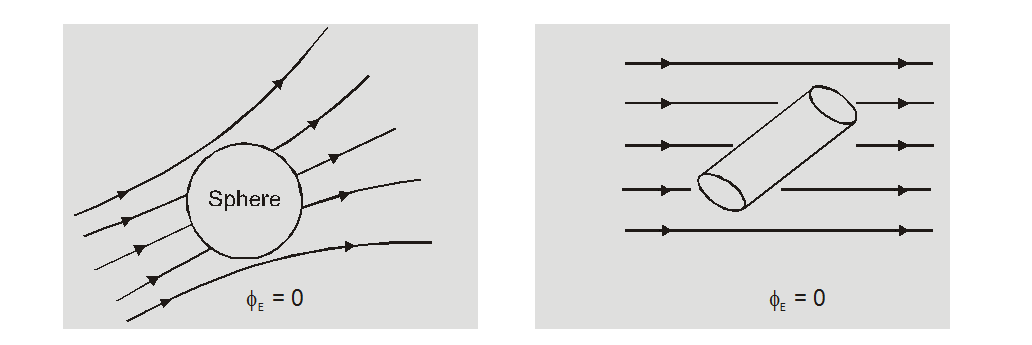
(ii) If a closed body encloses a charge q, total flux linked with the body is independent of the shape and size of the body and position of charge inside it.
Applications of Gauss law
Electric field due to a line charge:
Gauss law is useful in calculating electric field intensity due to symmetrical charge distributions.
We consider a gaussian surface which is a cylinder of radius r which encloses a line charge of length h with line charge density $\lambda$.
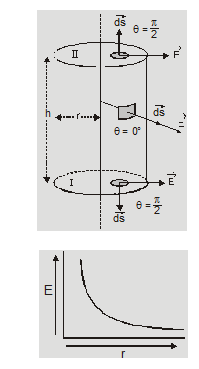
According to Gauss law
$\oint \vec{E} \cdot \overrightarrow{d s}=\frac{q_{i n}}{\varepsilon_{0}}$

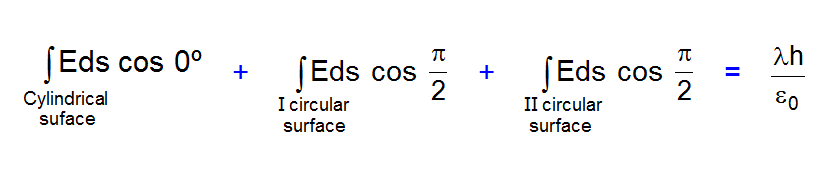
$E(2 \pi r h)=\frac{\lambda h}{\varepsilon_{0}}$
So
$E=\frac{\lambda}{2 \pi \varepsilon_{0} r} \quad\left(E \propto \frac{1}{r}\right)$
Electric field due to an infinite plane thin sheet of charge:
To find electric field due to the plane sheet of charge at any point P distant r from it, choose a cylinder of area of cross-section A through the point P as the Gaussian surface. The flux due to the electric field of the plane sheet of charge passes only through the two circular caps of the cylinder. Let surface charge density = $\sigma$
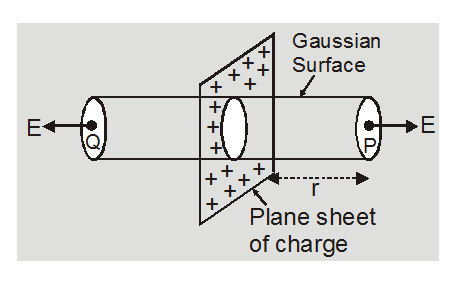
According to gauss law
$\oint \vec{E} \cdot \overrightarrow{d S}=q_{i n} / \varepsilon_{0}$
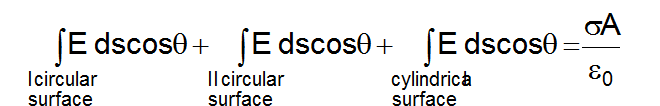
Or
$E A+E A+0=\frac{\sigma A}{2 \varepsilon_{0}}$
Or
$E=\frac{\sigma}{2 \varepsilon_{0}}$
Important Points
1. The magnitude of the electric field due to the infinite plane sheet of charge is independent of the distance from the sheet.
2. If the sheet is positively charged, the direction of the field is normal to the sheet and directed outward on both sides. But for a negatively charged sheet, the field is directed normally inwards on both sides of the sheet.
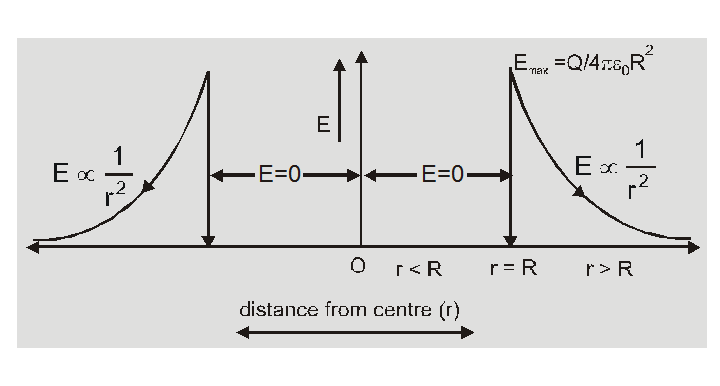
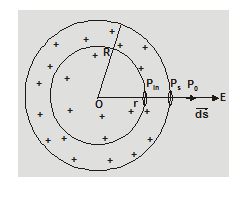
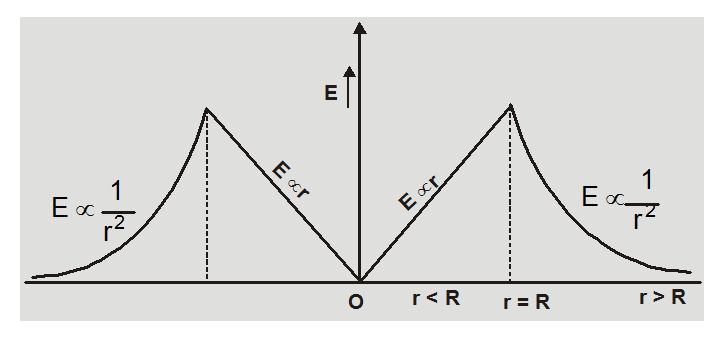
[3] Electric field intensity due to uniformly charged spherical shell:
We consider a thin shell of radius R carrying a charge Q on its surface
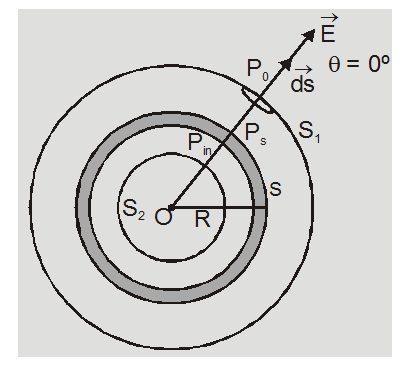
1. At a point P0 outside the shell (r > R)
According to gauss law
$\oint_{S_{1}} \overrightarrow{E_{0}} \cdot \overrightarrow{d s}=\frac{Q}{\varepsilon_{0}}$
Or
$\mathrm{E}_{0}\left(4 \pi \mathrm{r}^{2}\right)=\frac{\mathrm{Q}}{\varepsilon_{0}}$
$\mathrm{E}_{0}=\frac{\mathrm{Q}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}$
$=\frac{\sigma}{\varepsilon_{0}} \frac{R^{2}}{r^{2}}$
where the surface charge density
$\sigma=\frac{\text { total charge }}{\text { surface area }}$
$=\frac{Q}{4 \pi R^{2}}$
The electric field at any point outside the shell is same as if the entire charge is concentrated at center of shell.
2. At a point $P_{s}$ on surface of shell $(r=R)$
$E_{S}=\frac{Q}{4 \pi \varepsilon_{0} R^{2}}=\frac{\sigma}{\varepsilon_{0}}$
3. At a point $P_{\text {in }}$ inside the shell $(r According to gauss law $\oint_{S_{2}} \vec{E} \cdot \overrightarrow{d s}=\frac{q_{i n}}{\varepsilon_{0}}$ As enclosed charge $q_{\text {in }}=0$ So $\quad E_{\text {in }}=0$ The electric field inside the spherical shell is always zero. [4] Electric field intensity due to a spherical uniformly charge distribution : We consider a spherical uniformly charge distribution of radius R in which total charge Q is uniformly distributed throughout the volume. The charge density $\rho=\frac{\text { total charge }}{\text { total volume }}$ $=\frac{Q}{\frac{4}{3} \pi R^{3}}=\frac{3 Q}{4 \pi R^{3}}$ 1. At a point $P_{0}$ outside the sphere $(r>R)$ according to gauss law $\oint \vec{E}_{0} \cdot \overrightarrow{d s}=\frac{Q}{\varepsilon_{0}}$ $E_{0}\left(4 \pi r^{2}\right)=\frac{Q}{\varepsilon_{0}}$ Or $\mathrm{E}_{0}=\frac{\mathrm{Q}}{4 \pi \varepsilon_{0} \mathrm{r}^{2}}$ $=\frac{\rho}{3 \varepsilon_{0}}\left(\frac{\mathrm{R}^{3}}{\mathrm{r}^{2}}\right)$ 2. At a point $P_{s}$ on surface of sphere $(r=R)$ $\mathrm{E}_{\mathrm{s}}=\frac{\mathrm{Q}}{4 \pi \varepsilon_{0} \mathrm{R}^{2}}$ $=\frac{\rho}{3 \varepsilon_{0}} R$ 3. At a point $P_{\text {in }}$ inside the sphere $(r According to gauss law $\oint \vec{E}_{i n} \cdot \overrightarrow{d s}=\frac{q_{i n}}{\varepsilon_{0}}$ $=\frac{1}{\varepsilon_{0}} \rho \cdot \frac{4}{3} \pi r^{3}$ $=\frac{Q r^{3}}{\varepsilon_{0} R^{3}}$ $E_{\text {in }}\left(4 \pi r^{2}\right)=\frac{Q r^{3}}{\varepsilon_{0} R^{3}}$ or $E_{i n}=\frac{Q r}{4 \pi \varepsilon_{0} R^{3}}$ $=\frac{\rho}{3 \varepsilon_{0}} \mathrm{r}$ $\left(E_{\text {in }} \propto r\right)$ So, that's all from this article. I hope you get the idea about Gauss law in electrostatics. If you liked this article then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below. For a better understanding of this chapter, please check the detailed notes of the Electric charge and Fields. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.