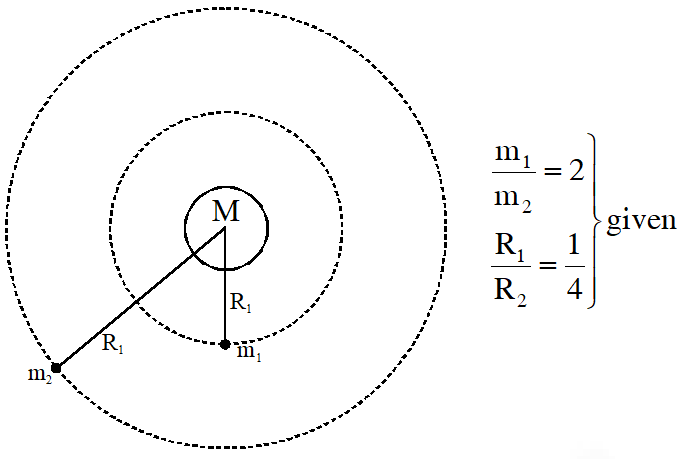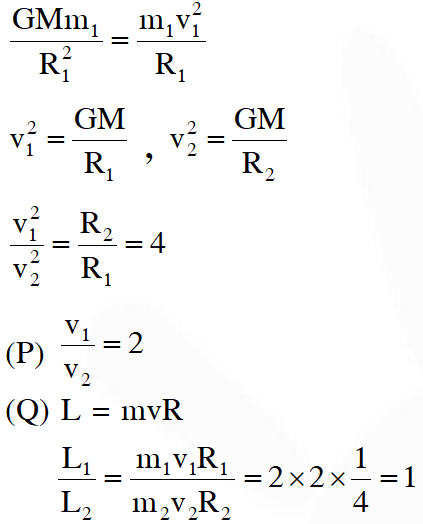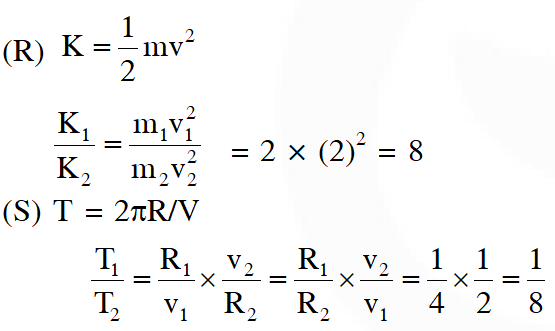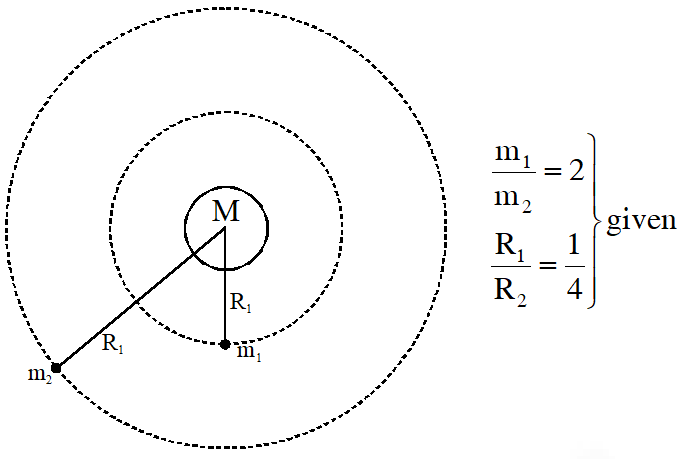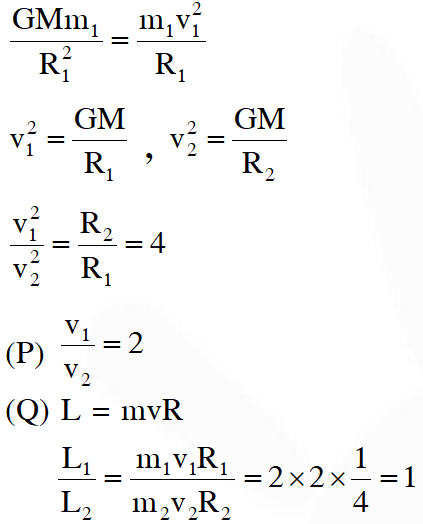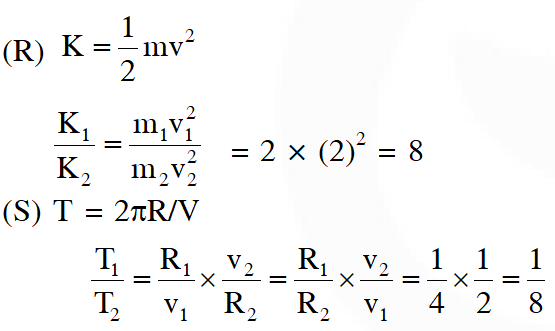JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Download eSaral app for free study material and video tutorials.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Simulator
Previous Years JEE Advanced Questions
Q. Gravitational acceleration on the surface of a planet is \frac{\sqrt{6}}{11} \mathrm{g}, where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is \frac{2}{3} times that of the Earth. If the escape speed on the surface of the earth is taken to be 11 \mathrm{kms}^{-1}, the escape speed on the surface of the planet in \mathrm{kms}^{-1}will be -
[IIT-JEE 2010]
Ans. 3
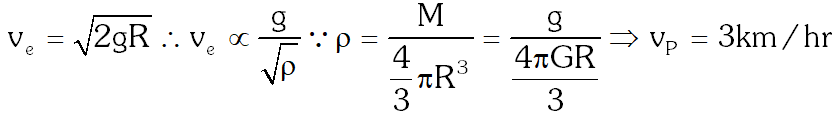
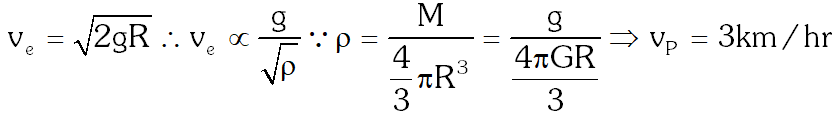
Q. A binary star consists of two stars A \left(\operatorname{mass} 2.2 \mathrm{M}_{\mathrm{s}}\right) \text { and } \mathrm{B}\left(\mathrm{mass} 11 \mathrm{M}_{\mathrm{s}}\right), where MS is the mass of the sun. They are separated by distance d and are rotating about their centre of mass, which is stationary. The ratio of the total angular momentum of the binary star to the angular momentum of star B about the centre of mass is -
[IIT-JEE 2010]
Ans. 6
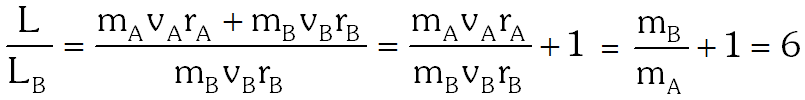
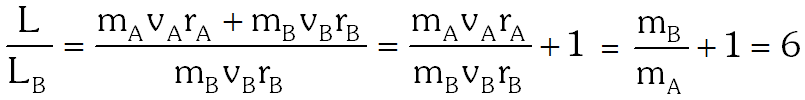
Q. A thin uniform annular disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is
[IIT-JEE 2010]
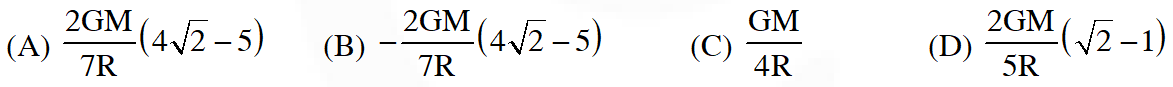[IIT-JEE 2010]
Ans. (A)
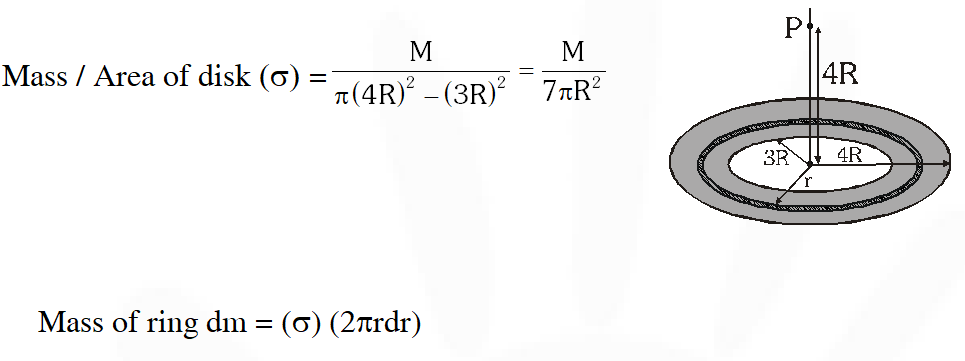
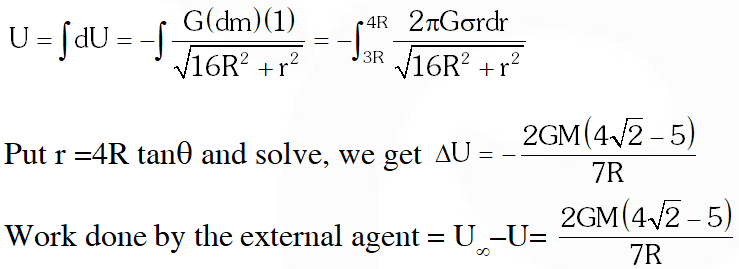
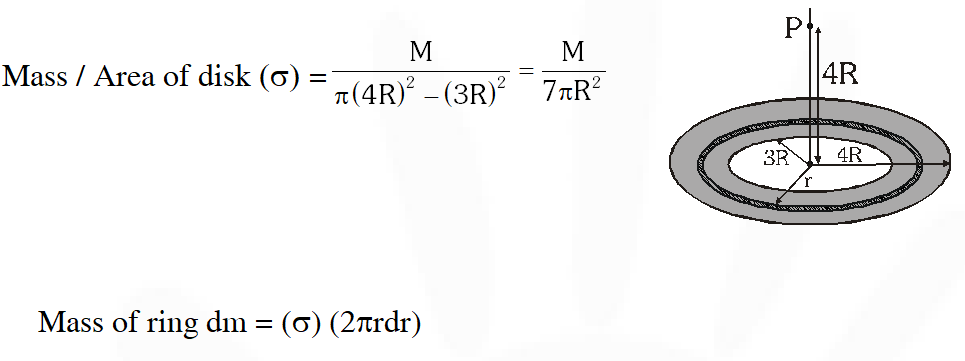
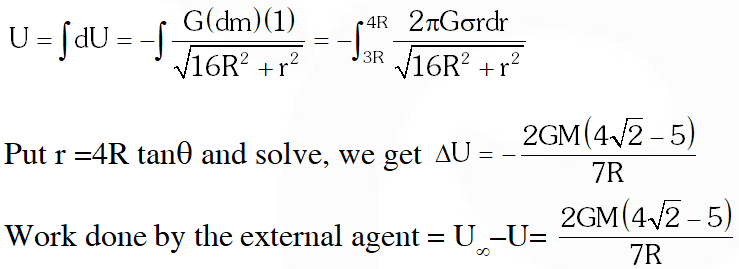
Q. A satellite is moving with a constant speed V in a circular orbit about the earth. An object of mass ‘m’ is ejected from the satellite such that it just escapes from the gravitational pull of the earth. At the time of its ejection, the kinetic energy of the object is :
[IIT-JEE 2011]
[IIT-JEE 2011]
Ans. (B)
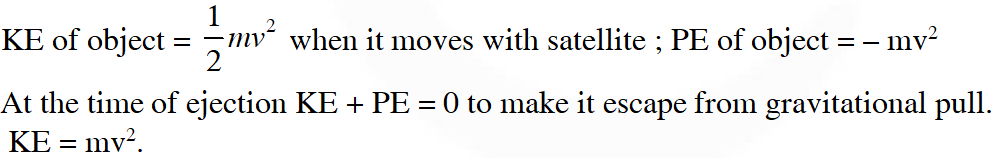
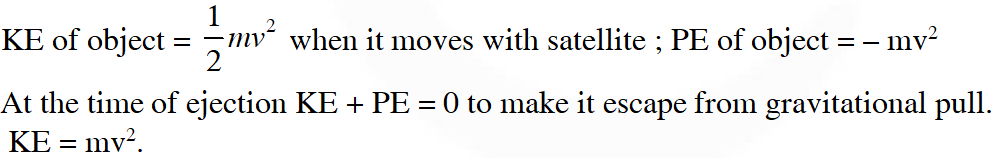
Q. Two spherical planets P and Q have the same uniform density , masses $\mathbf{M}_{\mathrm{p}}$ and $\mathbf{M}_{\mathrm{Q}}$, and surface areas A and 4A, respectively. A spherical planet R also has uniform density and its mass is ($\mathrm{M}_{\mathrm{p}}$ + $\mathbf{M}_{\mathrm{Q}}$). The escape velocities from the planets P, Q and R, are $\mathrm{V}_{\mathrm{p}}, \mathrm{V}_{\mathrm{Q}}$ and $\mathrm{V}_{\mathrm{R}}$, respectively. Then
(A) $\mathrm{V}_{\mathrm{Q}}>\mathrm{V}_{\mathrm{R}}>\mathrm{V}_{\mathrm{P}}$
(B) $\mathrm{V}_{\mathrm{R}}>\mathrm{V}_{\mathrm{Q}}>\mathrm{V}_{\mathrm{P}}$
(C) $\mathrm{V}_{\mathrm{R}} / \mathrm{V}_{\mathrm{P}}=3$
(D) $\mathrm{V}_{\mathrm{P}} / \mathrm{V}_{\mathrm{Q}}=1 / 2$
[IIT-JEE 2012]
Ans. (B,D)
Escape velocity $=\sqrt{\frac{2 G M}{R}} \propto \sqrt{\frac{4}{3} \pi R^{3}} \propto \sqrt{A r e a}$
[since density of each planet is same]
Q. A planet of radius $\mathrm{R}=\frac{1}{10} \times(\text { radius of Earth })$ has the same mass density as Earth. Scientists dig a well of depth on it and lower a wire of the same length and of linear mass density $10^{-3}$ $\mathrm{kgm}^{-1}$ into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it in place is (take the radius of Earth = $6 \times 10^{6}$ m and the acceleration due to gravity on Earth is $10 \mathrm{ms}^{-2}$) –
(A) 96 N (B) 108 N (C) 120 N (D) 150 N
[JEE-Advance 2014]
Ans. (B)
$\mathrm{E}_{\mathrm{G}}=\frac{4 \pi \mathrm{Gr} \rho}{3}$
$\mathrm{dF}=\mathrm{E}_{\mathrm{G}} \lambda \mathrm{dr}$
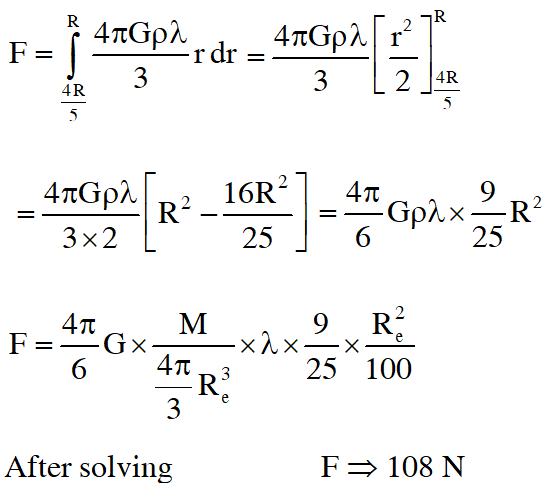
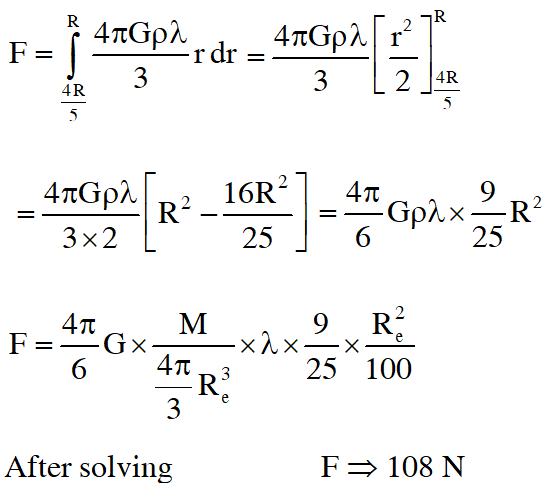
Q. A rocket is launched normal to the surface of the Earth, away from the Sun, along the line joining the sun and the Earth. The Sun is $3 \times 10^{5}$ times heavier than the Earth and is at a distance $2.5 \times 10^{4}$ times larger than the radius of the Earth. The escape velocity from Earth's gravitational field is $\mathrm{v}_{\mathrm{e}}=11.2 \mathrm{km} \mathrm{s}^{-1}$. The minimum initial velocity (vs) required for the rocket to be able to leave the Sun-Earth system is closest to (Ignore the rotation and revolution of the Earth and the presence of any other planet)
(A) $\mathrm{v}_{\mathrm{s}}=22 \mathrm{km} \mathrm{s}^{-1}$
(B) $\mathrm{v}_{\mathrm{s}}=72 \mathrm{km} \mathrm{s}^{-1}$
(C) $\mathrm{v}_{\mathrm{s}}=42 \mathrm{km} \mathrm{s}^{-1}$
(D) $\mathrm{v}_{\mathrm{s}}=62 \mathrm{km} \mathrm{s}^{-1}$
[JEE-Advance 2017]
Ans. (C)
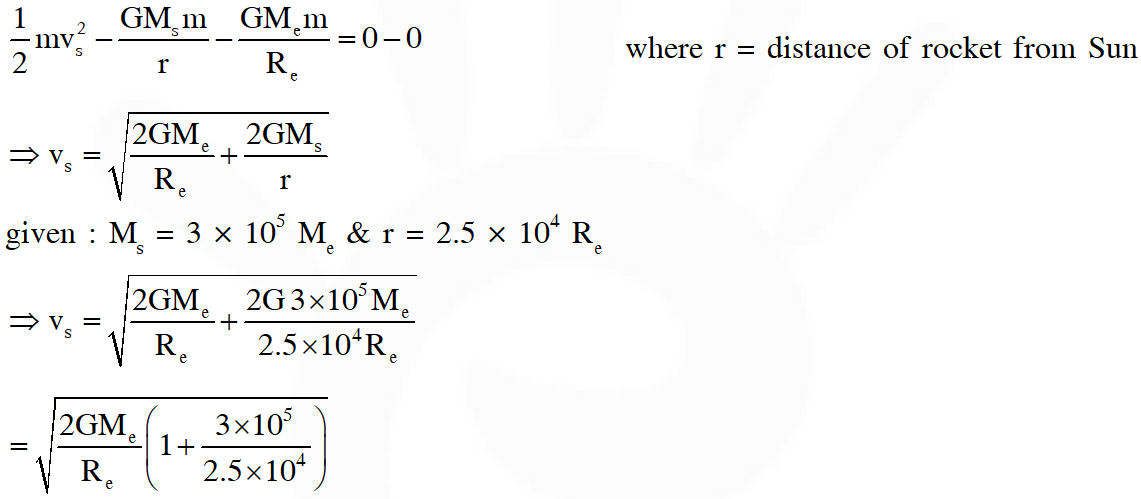
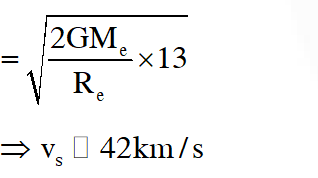
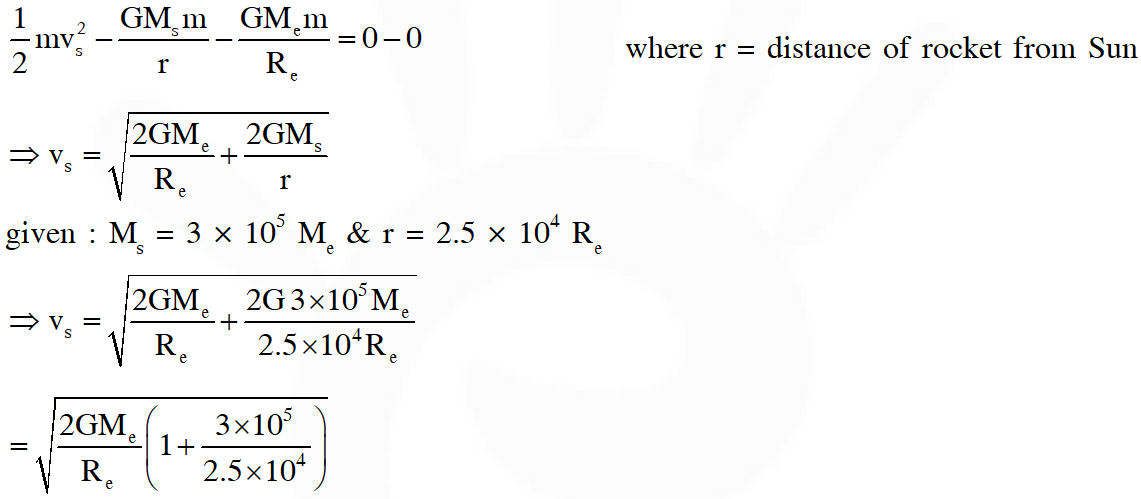
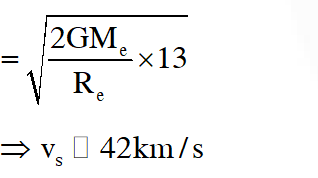
Q. A planet of mass M, has two natural satellites with masses $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$. The radii of their circular orbits are $\mathrm{R}_{1}$ and $\mathrm{R}_{2}$ respectively. Ignore the gravitational force between the satellites. Define $\mathrm{v}_{1}, \mathrm{L}_{1}, \mathrm{K}_{1}$ and $\mathrm{T}_{1}$ to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 ; and $\mathrm{v}_{2}, \mathrm{L}_{2}, \mathrm{K}_{2}$ and $\mathrm{T}_{2}$ to be the corresponding quantities of satellite 2. Given $\mathrm{m}_{1} / \mathrm{m}_{2}=$ 2 and $\mathrm{R}_{1} / \mathrm{R}_{2}=1 / 4$, match the ratios in List-I to the numbers in List-II.
[JEE-Advance 2018]
[JEE-Advance 2018]
Ans. (B)
