JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. $\mathrm{ABCD}$ is a trapezium such that $\mathrm{AB}$ and $\mathrm{CD}$ are parallel and $\mathrm{BC} \perp \mathrm{CD} .$ If $\angle \mathrm{ADB}=\theta, \mathrm{BC}=$
$\mathrm{p}$ and $\mathrm{CD}=\mathrm{q},$ then $\mathrm{AB}$ is equal to
(1) $\frac{\left(p^{2}+q^{2}\right) \sin \theta}{p \cos \theta+q \sin \theta}$
(2) $\frac{p^{2}+q^{2} \cos \theta}{p \cos \theta+q \sin \theta}$
(3) $\frac{p^{2}+q^{2}}{p^{2} \cos \theta+q^{2} \sin \theta}$
(4) $\frac{\left(p^{2}+q^{2}\right) \sin \theta}{(p \cos \theta+q \sin \theta)^{2}}$
[JEE-MAINS-2013]
Ans. (1)
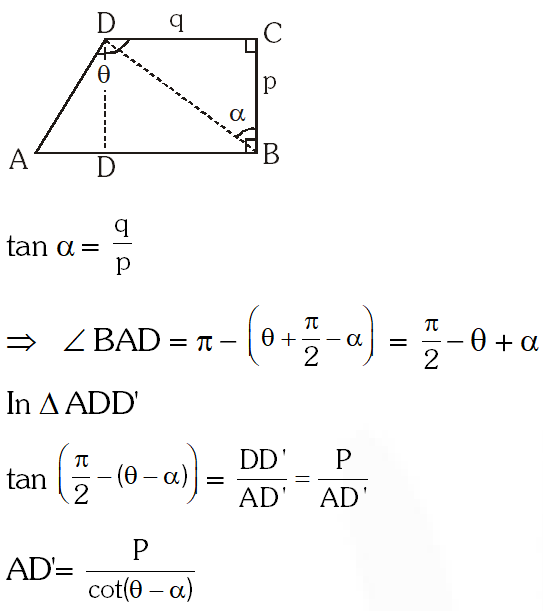
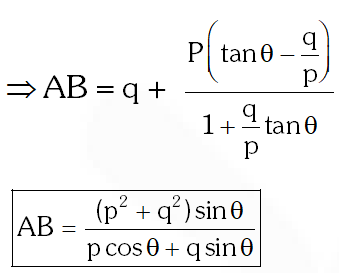
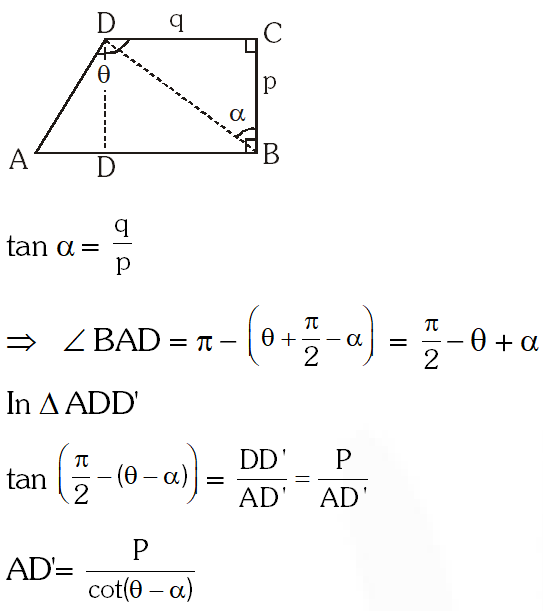
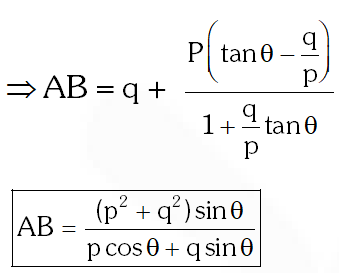
Q. If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are $30^{\circ}, 45^{\circ}$ and $60^{\circ}$ respectively, then the ratio, AB : BC, is:
(1) $1: \sqrt{3}$
(2) 2 : 3
(3) $\sqrt{3}: 1$
(4) $\sqrt{3}: \sqrt{2}$
[JEE(Main)-2015]
Ans. (3)
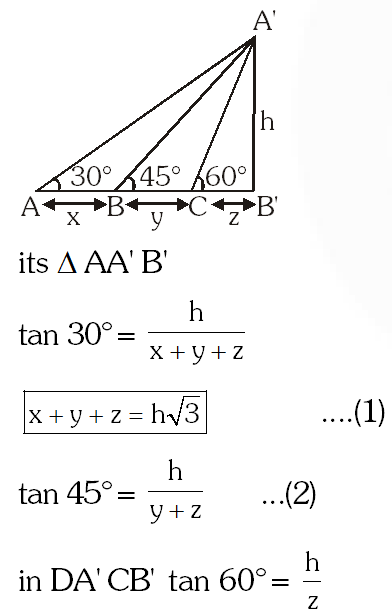
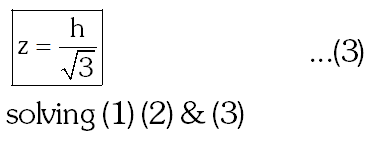
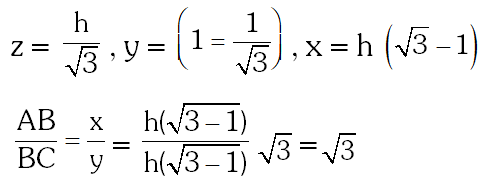
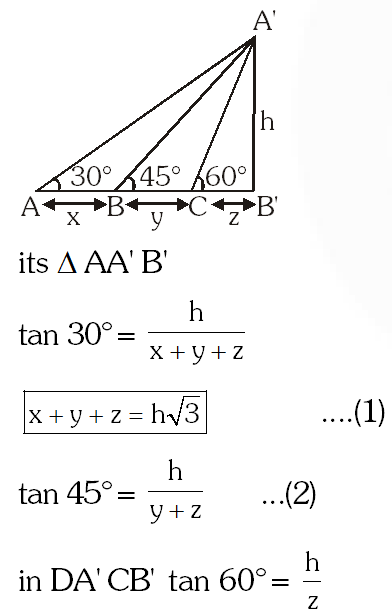
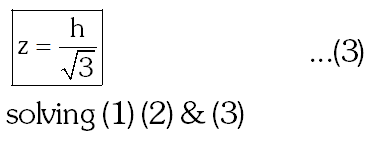
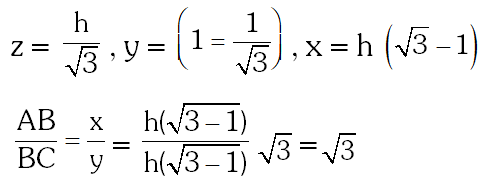
Q. A man is walking towards a vertical pillar in a straight path, at a uniform speed. Then the time taken (in minutes) by him, form B to reach the pillar, is :
(1) 5 (2) 6 (3) 10 (4) 20
[JEE(Main)-2016]
Ans. (1)
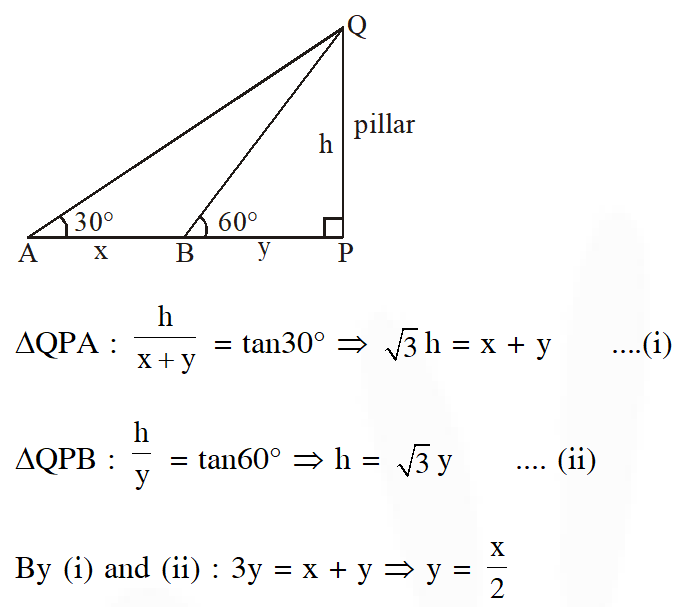
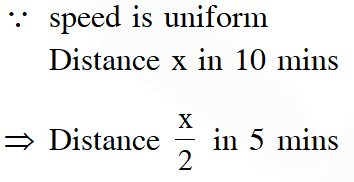
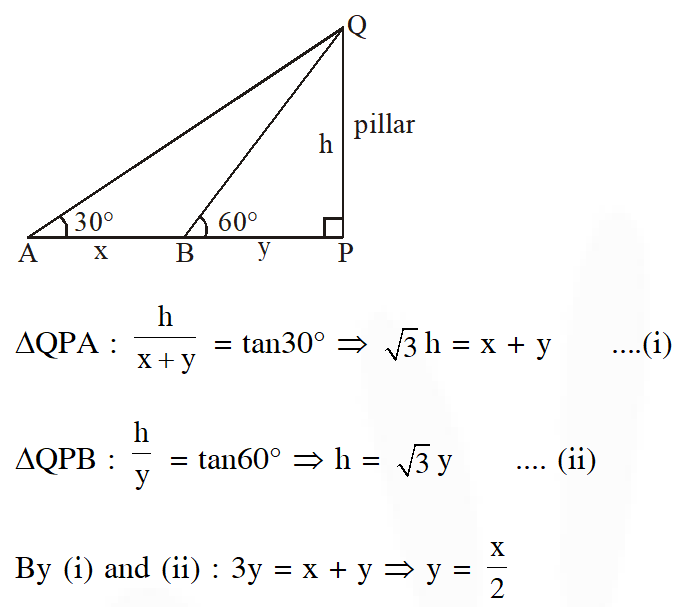
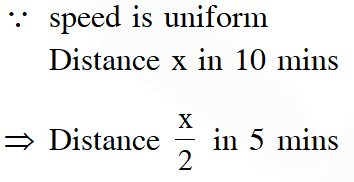
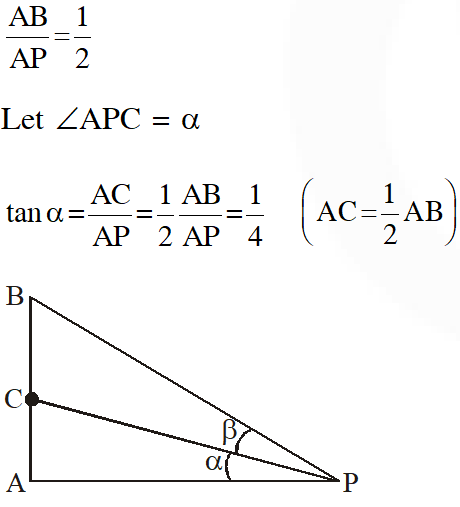
Q. Let a vertical tower AB have its end A on the level ground. Let C be the mid-point tanis equal to :-
(1) $\frac{4}{9}$
(2) $\frac{6}{7}$
(3) $\frac{1}{4}$
(4) $\frac{2}{9}$
[JEE(Main)-2017]
Ans. (4)
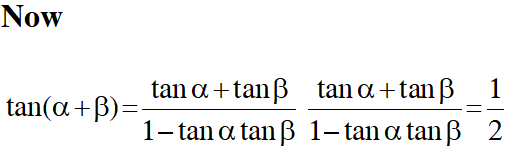
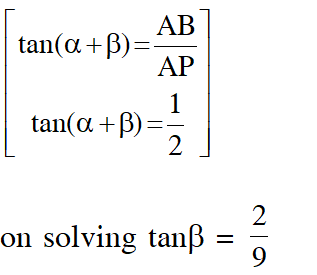

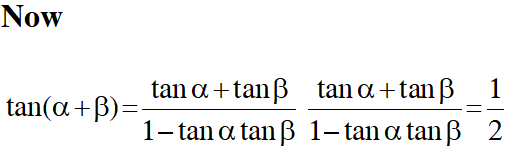
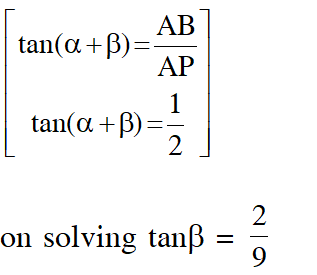
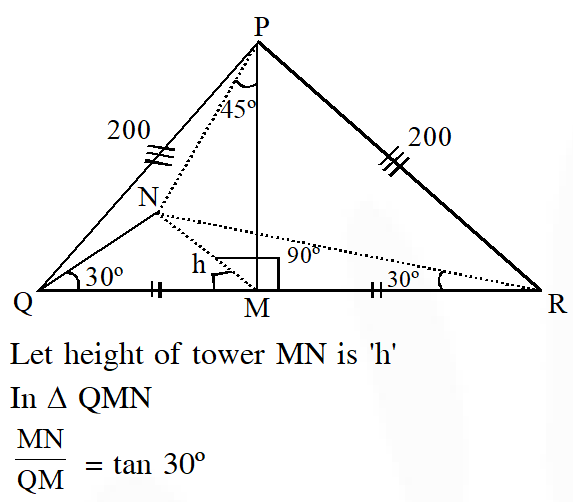
Q. PQR is a triangular park with $\mathrm{PQ}=200 \mathrm{m}$. A T.V. tower stands at the mid-point of $\mathrm{QR} .$ If the angles of elevation of the top of the tower at $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ are respectively $45^{\circ},$ $\left.30^{\circ} \text { and } 30^{\circ}, \text { then the height of the tower (in } \mathrm{m}\right)$ is-
(1) 50
(2) $100 \sqrt{3}$
(3) $50 \sqrt{2}$
(4) 100
[JEE(Main)-2018]
Ans. (4)
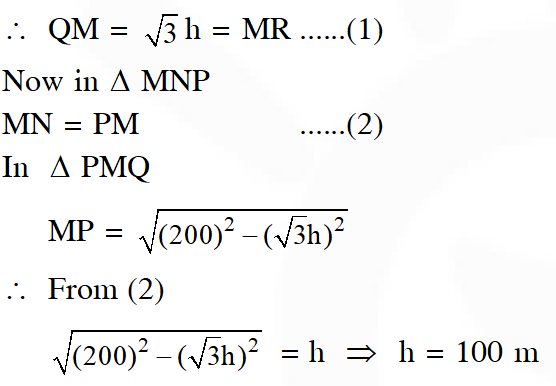

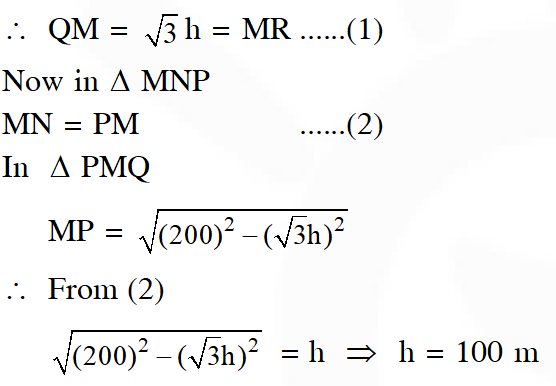
Comments
Alekhya
June 3, 2020, 12:58 p.m.
sir this esaral is providing a very gud set of questions...
but its need to update a little, we the students are ariving 2020 jee and for that we need latest jee online questions.
these questions are just incomplete
