Horizontal Projectile motion - Motion in Plane - eSaral

Hey, do you want to learn about Horizontal projectile motion? If yes. Then you are at the right place.

Horizontal Projectile motion

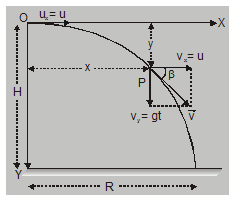
Suppose a body is thrown horizontally from point O, with velocity u. Height of O from ground = H. Let X-axis be along horizontal and Y-axis be vertically downwards and origin O is at point of projection as shown in fig. Let the particle be at P at a time t. The co-ordinates of P are (x, y) Distance travelled along X-axis at time t with uniform velocity i.e. Velocity of projection and without acceleration.



The horizontal component of velocity $\mathrm{V}_{\mathrm{x}}$ = u

and horizontal displacement x = u . t….(1)

to calculate y, consider vertical motion of the projectile

initial velocity in vertical direction $\mathrm{u}_{\mathrm{y}}$ = 0.

acceleration along y direction $a_{y}$ = g (acc. due to gravity)

so

$v_{v}=a_{y} t$

(y comp. of velocity at time t)

Or

$v_{y}=g t$....(2)

(as body were dropped from a height)

Resultant velocity at time t is

$\overrightarrow{\mathrm{v}}=\mathrm{u} \hat{\mathrm{i}}+(\mathrm{gt}) \hat{\mathrm{j}}$

$v=\sqrt{u^{2}+(g t)^{2}}$

if $\beta$ is the angle of velocity with X-axis (horizontal) $\tan \beta=\frac{\mathrm{gt}}{\mathrm{u}}$

and

$y=\frac{1}{2} g t^{2}$......(3)

Or

$y=\frac{1}{2} g\left(\frac{x}{u}\right)^{2}$

[from equation (i) $\left.\mathrm{t}=\frac{\mathrm{x}}{\mathrm{u}}\right]$

Or

$y=\frac{g}{2 u^{2}} \cdot x^{2}$

Or

$y=k x^{2}$

here $\mathrm{k}=\frac{\mathrm{g}}{2 \mathrm{u}^{2}} \quad(\mathrm{k}$ is constant)

This is eqn. of a parabola.

A body thrown horizontally from a certain height above the ground follows a parabolic trajectory till it hits the ground.

1. Time of flight$\mathrm{T}=\sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$ [as $\left.\mathrm{y}=\frac{1}{2} \mathrm{gt}^{2}, \mathrm{~T}=\sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}\right]$


2. Range horizontal distance covered = R.R = u × time of flight$\mathrm{R}=\mathrm{u} \cdot \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$
   
   $\left[\because \mathrm{H}=\frac{\mathrm{g}}{2 \mathrm{u}^{2}} \mathrm{R}^{2}\right]$


3. Velocity when it hits the ground$\mathrm{v}_{\mathrm{g}}=\sqrt{\mathrm{u}^{2}+2 \mathrm{gH}}$

So, that's all from this blog, I hope you get the idea about the Horizontal projectile motion. If you found this article helpful then please share it with your friends.

Also, read
Oblique Projectile motion

To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.