Hey, do you want to learn about the interference by thin films? If so. Then you are at the right place.
Interference by Thin Films
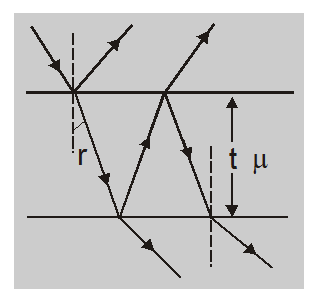
The interference caused by thin films is due to the interference between the waves reflected from the upper and lower surfaces. These two reflected coherent waves are obtained from the same incident wave by division of amplitude.
A film of thickness t and refractive index $\mu$ produces a path difference of $2 \mu \mathrm{cos} \mathrm {r}$ between the two reflected waves and an additional path difference $\frac{\lambda}{2}$
or phase difference of $\pi$ is produced due to the reflection of one wave from a denser medium. Thus, the total path difference in reflected waves is $\left(2 \mu t \cos r+\frac{\lambda}{2}\right)$
For maxima $2 \mu t \quad \cos r+\frac{\lambda}{2}=n \lambda$
or $2 \mu t \cos r=(2 n-1) \frac{\lambda}{2}$
and for minima $2 \mu t \cos r+\frac{\lambda}{2}=(2 n+1) \frac{\lambda}{2}$
or $2 \mu t \cos r=(2 n-1) \frac{\lambda}{2}$
Here r is the angle of refraction. For normal incidence or near-normal incidence $r \approx 0$ ,so that
for maxima $2 \mu t=(2 n \pm 1) \frac{\lambda}{2}$
for minima $2 \mu t=n \lambda$ If a film is very thin $t \approx 0$, then the condition of minima is satisfied and the film appears dark in reflected light.
In transmitted waves, similar interference is observed, but now the additional path difference of $\frac{\lambda}{2}$ is absent. So, in transmitted waves.
$2 \mu t \cos r=n \lambda$ for maxima
and $2 \mu t \cos r=(2 n \pm 1) \frac{\lambda}{2}$ for minima.
Points to remember
- The fringe width increases with the increase in distance between the source & the screen.
- Fringe width decreases by increasing distance between two slits $s_{1} \& s_{2}$.
- If the experiment is repeated in water instead of air, then $\beta$ decreases.
- When one of the slits of $s_{1} \& s_{2}$ is close then interference does not take place.
- When the two slits are illuminated by two independent sources then interference fringes are not obtained.
- When one of the slits is closed & the width of another is made of the order of $\lambda$, then diffraction fringes are observed
- When the slit is illuminated with different colors then fringes are obtained of the same color but their fringes width is different.
- In young's double-slit experiment light waves undergo diffraction at both the slits and the diffracted waves superimpose to produce interference.
- If biprism experiment is a liquid instead of air, then the fringe width increases (whereas in young's double-slit experiment it decreases)
- The wavelength undergoing destructive interference, the color of that wavelength will be absent.
- The wavelength for which the condition of constructive interference is fulfilled that color will be visible maximum consequently the fringes will be colored.
so, that's all from this article. I hope you get the idea about the Interference by Thin Films. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of the Wave Optics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
