JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Let $\mathrm{L}=\lim _{x \rightarrow 0} \frac{\mathrm{a}-\sqrt{\mathrm{a}^{2}-\mathrm{x}^{2}}-\frac{\mathrm{x}^{2}}{4}}{\mathrm{x}^{4}}, \mathrm{a}>0 .$ If $\mathrm{L}$ is finite, then $:-$
(A) a = 2
(B) a = 1
(C) $\mathrm{L}=\frac{1}{64}$
(D) $\mathrm{L}=\frac{1}{32}$
[JEE 2009, 4]
Ans. (A,C)
$\mathrm{a}-\mathrm{a}\left(1-\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}\right)^{\frac{1}{2}}-\frac{\mathrm{x}^{2}}{4} \quad \mathrm{a}-\mathrm{a}\left(1-\frac{\mathrm{x}^{2}}{2 \mathrm{a}^{2}}-\frac{1}{8} \frac{\mathrm{x}^{4}}{\mathrm{a}^{4}}\right)-\frac{\mathrm{x}^{2}}{4}$
$\mathrm{a}=2,\left(\mathrm{coefficient} \text { of } \mathrm{x}^{2}=0\right)$
$\therefore \mathrm{L}=\frac{1}{64}$
Q. If $\lim _{x \rightarrow 0}\left[1+x \ell n\left(1+b^{2}\right)\right]^{\frac{1}{x}}=2 b \sin ^{2} \theta, b>0$ and $\theta \in(-\pi, \pi],$ then the value of $\theta$ is-
 [JEE 2011, 3M, –1M]
[JEE 2011, 3M, –1M]
 [JEE 2011, 3M, –1M]
[JEE 2011, 3M, –1M]
Ans. (D)
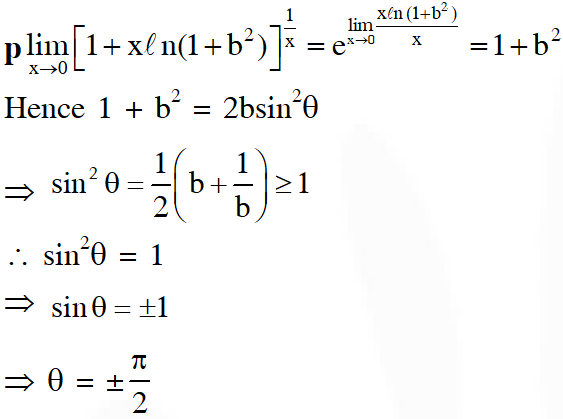
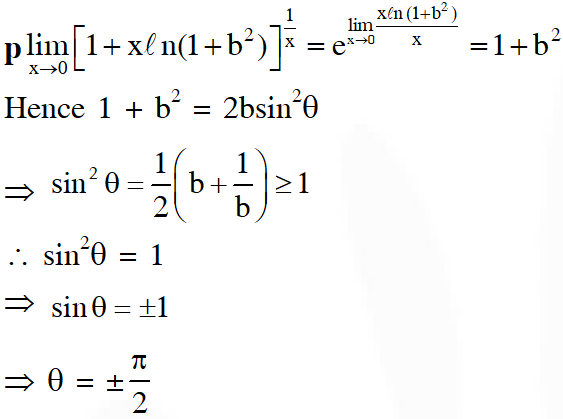
Q. If $\lim _{x \rightarrow \infty}\left(\frac{x^{2}+x+1}{x+1}-a x-b\right)=4,$ then $-$
(A) a = 1, b = 4 (B) a = 1, b = –4] (C) a = 2, b = –3 (D) a = 2, b = 3
[JEE 2012, 3M, –1M]
Ans. (B)


Q. Let $\alpha(\mathrm{a})$ and $\beta(\mathrm{a})$ be the roots of the equation $(\sqrt[3]{1+a}-1) x^{2}+(\sqrt{1+a}-1) x+(\sqrt[6]{1+a}-1)=0$ where $a>-1 .$ Then $\lim _{a \rightarrow 0^{+}} \alpha(a)$ and $\lim _{a \rightarrow 0^{+}} \beta(a)$ are
(A) $-\frac{5}{2}$ and 1
(B) $-\frac{1}{2}$ and $-1$
(C) $-\frac{7}{2}$ and 2
(D) $-\frac{9}{2}$ and 3
[JEE 2012, 3M, –1M]
Ans. (B)




Q. The largest value of the non-negative integer a for which $\lim _{x \rightarrow 1}\left\{\frac{-a x+\sin (x-1)+a}{x+\sin (x-1)-1}\right\}^{\frac{1-x}{1-\sqrt{x}}}=\frac{1}{4}$ is
[JEE(Advanced)-2014, 3]
Ans. 0




Q. Let $\alpha, \beta \in \mathrm{R}$ be such that $\lim _{x \rightarrow 0} \frac{x^{2} \sin (\beta x)}{\alpha x-\sin x}=1 .$ Then $6(\alpha+\beta)$ equals
[JEE(Advanced)-2016]
Ans. 7


Q. Let $\mathrm{f}(\mathrm{x})=\frac{1-\mathrm{x}(1+|1-\mathrm{x}|)}{|1-\mathrm{x}|} \cos \left(\frac{1}{1-\mathrm{x}}\right)$ for $\mathrm{x} \neq 1 .$ Then
 [JEE(Advanced)-2017]
[JEE(Advanced)-2017]
 [JEE(Advanced)-2017]
[JEE(Advanced)-2017]
Ans. (A,C)


Q. For any positive integer n, define $f_{\mathrm{n}}:(0, \infty) \rightarrow \square$ as $f_{\mathrm{n}}(\mathrm{x})=\sum_{\mathrm{j}=1}^{\mathrm{n}} \tan ^{-1}\left(\frac{1}{1+(\mathrm{x}+\mathrm{j})(\mathrm{x}+\mathrm{j}-1)}\right)$ for all $\mathrm{x} \in(0, \infty)$
(Here, the inverse trigonometric function $\tan ^{-1} \mathrm{x}$ assume values in $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) .$ )
Then, which of the following statement(s) is (are) TRUE?
(A) $\sum_{j=1}^{5} \tan ^{2}\left(f_{j}(0)\right)=55$
(B) $\sum_{j=1}^{10}\left(1+f_{j}^{\prime}(0)\right) \sec ^{2}\left(f_{j}(0)\right)=10$
(C) For any fixed positive integer $n, \lim _{x \rightarrow \infty} \tan \left(f_{\mathrm{n}}(x)\right)=\frac{1}{n}$
(D) For any fixed positive integer $n, \operatorname{limsec}_{x \rightarrow \infty} \operatorname{ec}^{2}\left(f_{\mathrm{n}}(x)\right)=1$
[JEE(Advanced)-2018]
Ans. (D)




Q. For each positive integer $n,$ let $y_{n}=\frac{1}{n}(n+1)(n+2) \ldots(n+n)^{1 / n}$ For $x \in \square,$ let $[x]$ be the greatest integer less than or equal to $x$. If $\lim _{n \rightarrow \infty} y_{n}=L,$ then the value of $[L]$ is
[JEE(Advanced)-2018]
Ans. 1





Comments
renu
Aug. 16, 2021, 5:47 p.m.
for last 4th question the best approach is to use expansions ... it will make it very simple .
Anonymous
Feb. 11, 2021, 7:24 p.m.
Preferably....make some appropriation in the website and thank you for the questions despite of those problems.. keep it it up buddy
Vivek
Aug. 16, 2020, 10:13 p.m.
For anyone having problems seeing the questions, right-click on the equation part, click “Show Math as”, then click “MathML code”. Copy all the text in the new window that opens with Ctrl+A. Now open a new tab and type in this URL: http://www.wiris.com/editor/demo/en/developers. And paste whatever you copied! Woila! Thank me later!
