Get linear momentum questions and answers for Board exams. View 11th Physics important questions for exam point of view. These important questions with answers will play significant role in clearing concepts of Conservation of Linear Momentum Principles. This question bank is designed by expert and experienced IITian faculties keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions with answers for class 11 Physics chapters . Click Here for Detailed Notes of Conservation of Linear Momentum Principles along with chapters and Subjects.
Q. "The total momentum in the universe remains constant'.'. Is this statement true? If so, why?
Ans. since no external force can be applied on the universe, therefore total momentum is conserved.
Q. A box, initially sliding on the floor of a room, is eventually brought to rest by friction. Is the momentum of the box conserved? If not, does this process contradict the principle of conservation of momentum? What becomes of original momentum of the box?
Ans. No; No; transferred to earth.
Q. A meteorite burns in the atmosphere before it reaches the Earth's surface. What happens to its momentum?
Ans. The momentum will be transferred to the air particles and finally to the earth.
Q. Does relative velocity of separation in one dimensional elastic collision change?
Ans. In one dimensional elastic collision relative velocity of separation after collision is equal to relative velocity of approach before collision.
Q. What happens when two bodies of equal masses undergo elastic collision in one dimension?
Ans. Their velocities are just interchanged. This result has an important application in a nuclear reaction.
Q. Is linear momentum of a system always conserved.
Ans. No, only when the system is isolated.
Q. The collision between two hydrogen atoms is perfectly elastic so the momentum is conserved do you agree with this statement.
Ans. No, because momentum is conserved even when collision is inelastic.
Q. Is it possible to have a collision in which the whole of K.E. is lost.
Ans. Yes, for example in perfectly inelastic collision of two bodies moving toward each other with equal linear momentum
Q. If two object collide and one is initially at rest (a) Is it possible for both to be at rest after collision. (b) Is it possible for any one to be at rest after collision.
Ans. (a) No, because momentum will not be conserved in that case. (b) Yes, when masses of two object are equal and collision is perfectly elastic.
Q. A meterorite burn in the atmosphere before it reach the earth's surface what happens to it momentum.
Ans. The momentum is transferred to the air molecules and the earth.
Q. Is centre of mass a reality?
Ans. No, It is only a mathematical concept.
Q. Give an example each for a body, where the centre of mass lies inside the body and outside the body.
Ans. Following are the two examples - (i) In case of solid sphere the centre of mass lie inside the body. (ii) In case of hollow sphere or ring the centre of mass lie out side the body.
Q. How does the centre of mass of an isolated system move?
Ans. The centre of mass of an isolated system moves with a constant velocity.
Q. A child sits stationary at one end of a long trolley moving uniformly with a speed $v$ on a smooth horizontal floor. If child gets up and runs about on the trolley in any manner, what is the speed of the C.M. of the (trolley + child) system? [NCERT]
Ans. The speed of the centre of mass of the system i.e. trolley and the child remains unchanged, if the child gets up and runs about on the trolley in any manner. It is because, the forces involved are from within the system, where as the state of the system can change only under the effect of an external force.
Q. Briefly explain the motion of centre of mass of earth-moon system.
Ans. The centre of mass of earth-moon system move in elliptical path round the sun. The system of earth- moon moves due to external force provided by the sun and the parts of the system under motion about COM is due to the internal force between them.
Q. Two men stand facing each other on two boats floating on still water at a short distance apart. A rope is held at its ends by both. The two boats are found to meet always at the same point, whether each man pulls separately or both pull together. Why ? Will the time taken be different in the two cases?Neglect friction.
Ans. The men on the two boats floating on water constitute a single system and the forces applied by them on each other are internal forces. When the man on the each boat pulls separately or both pull together, the center of mass of the system of boats remains fixed. It is because, centre of mass moves under the effect of external force only. Therefore, the two boats always meet at a fixed point, which is centre of mass of the system. It does not matter, whether each man pulls separately or both pull together. However, time taken in the two cases will not be same. The boats will take shorter time to meet, when both the men pull together.
Q. From a uniform circular disc of diameter $d,$ a circular hole of diameter $\mathrm{d} / 6$ and having its centre at a distance of $\mathrm{d} / 4$ from the centre of the disc is scoped out. Find the centre of mass of the remaining portion.
Ans. Let the mass per unit area of the disc be m. Then,
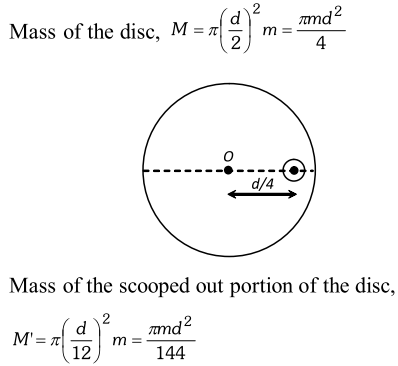
Q. A projectile is fired with a velocity $u$ at an angle to the horizontal. At the highest point, it breaks into two equal parts. If one part, retraces its path, what is the direction and velocity of the other part? Ans. Momentum at the highest point
Ans. 
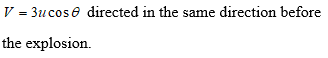
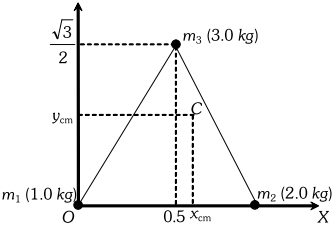
Q. Locate the centre of mass of a system of three particles of masses $1.0 \mathrm{kg}, 2.0 \mathrm{kg}$ and $3.0 \mathrm{kg}$ placed at the corners of an equilateral triangle of $1 \mathrm{metre}$side.
Q. A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei, the products must be emitted in opposite directions. [NCERT]
Ans. Applying principle of conservation of momentum, $m_{1} \vec{v}_{1}+m_{2} \vec{v}_{2}=0$ (Here, the letters have usual meanings) $\Rightarrow m_{2} \vec{v}_{2}=-m_{1} \vec{v}_{1}$ $\Rightarrow \vec{v}_{2}=-\frac{m_{1} \vec{v}_{1}}{m_{2}}$ The negative sign indicates that the products move in opposite directions.
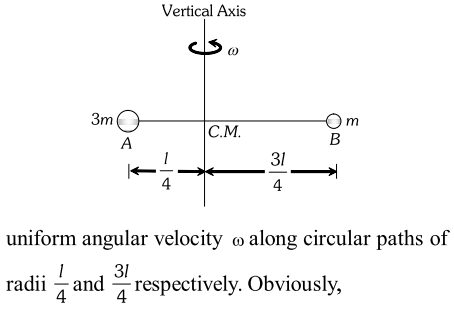
Q. (a) Two balls of masses $3 m$ and $m$ are separated by a distance $l .$ Find the position of the centre of mass. (b) If these two balls are attached to a vertical axis by means of two threads whose combined length is $l$ and rotated in a horizontal plane with uniform angular velocity $\omega$ about an axis of rotation passing $\mathrm{g}$ in the $\mathrm{g}$ in the through centre of mass, prove that tensions in the two strings will become equal.
Ans. (a) Let $x$ be the distance of centre of mass from the ball $A$ of mass $3 m[\text { Fig. }]$. Then, distance of the centre of mass from the ball $B$ will be $(l-x)$.
Q. A bag of sand of mass $M$ is hanging from a rope. A bullet of mass $\frac{\mathrm{M}}{\mathrm{x}}$ is fired at it with a velocity $v .$ The bullet gets embedded into the bag. What is the velocity of the bag after the bullet gets embedded into it?
Ans.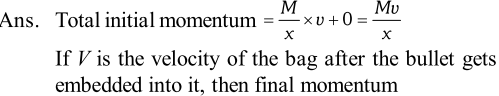 
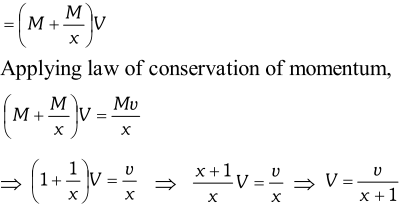
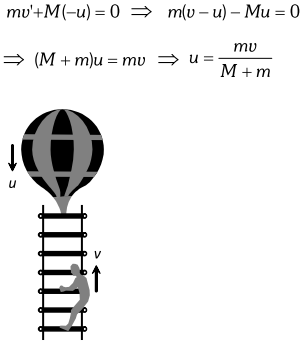
Q. A man of mass $m$ stands on a rope-ladder, which is tied to the free balloon of mass $M$ The balloon is initially at rest. In what direction and at what speed will the balloon move, if the man starts to climb the rope-ladder at a constant velocity $v$ relative to the ladder?
Ans. Initially, when the man stands on the rope-ladder, the system (man, balloon and rope-ladder) is at rest i.e. initial momentum of the system is zero. When the man climbs up the ladder, the force acting on the balloon and rope-ladder is an internal force.Therefore, total momentum of the system should still remain zero. Since man is climbing up, the balloon and the rope-ladder would descend. Let $u$ be the velocity of the balloon and rope-ladder w.r.t. earth in downward direction, when the man starts climbing up. Since velocity of the man w.r.t the earth, $v^{\prime}=v-u$ According to the principle of conservation of momentum,
Q. A rocket explodes in mid air how does this affect (a) Its total momentum (b) Its total kinetic energy.
Ans. (a) Because no external force acts on the rocket its total momentum remains unchanged. (b) When the rocket explodes its fragments receive additional kinetic energy from explosion (Chemical, energy of fuel changes into kinetic energy). As a result of this the total kinetic energy gets increased.
Q. The velocity of an aeroplane is doubled (a) What will happen to the momentum, will the momentum remain conserved. (b) What will happen to the kinetic energy will the energy remain conserved.
Ans. (a) When the velocity of aeroplane is doubled. Its momentum gets doubled but the momentum of air also gets increased by the same amount in opposite direction so that total momentum of plane and air remains conserved. (b) The kinetic energy will become four times additional energy will be obtained by burning of the fuel of the plane. In fact the total energy will remain conserved.
Q. In an elastic collision what happened to mechanical energy?
Ans. In an elastic collision the mechanical energy is not converted into any other form of energy and force of interaction are conservative in nature.
Q. What is the work done by resistive force of air on vibrating pendulum in bringing it to rest?
Ans. Work done is negative because the resistive force of air always act opposite of the direction of motion of the vibrating pendulum
Q. Is whole of the kinetic energy lost in any perfectly inelastic collision.
Ans. No, only that much amount of kinetic energy is lost as is necessary for the conservation of momentum.
Q. What is the energy associated with a bird flying in
Ans. A flying bird possesses both potential and kinetic energy as it is at a certain height above the groundand moving with certain velocity.
Q. A cake of mud is thrown on a wall where it sticks what happens to its initial kinetic energy.
Ans. A part of the kinetic energy is used deforming the cake and the remaining part converted into heat and sound energy.
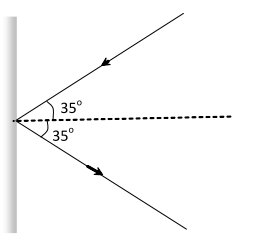
Q. A molecule in a gas container hits the wall with speed $100 \mathrm{m} / \mathrm{s}$ at an angle of $35^{\circ}$ with the normal and rebounds with the same speed. State whether linear momentum is conserved or not. What type of collision is it?
Ans. Linear momentum is always conserved whether the collision is elastic or inelastic. Thus in the given situation, momentum is conserved. As the speed of the molecules remains same after the collision, so kinetic energy of the molecules is also conserved. Hence, the collision is elastic.
Q. Is collision possible even without actual contact of the colliding particle?
Ans. Yes, such collision is called collision at a distance. The collision between subatomic particles (like proton and nucleus) are example of such collisions.
Q. The bob A of a simple pendulum released from $30^{\circ}$ to the vertical hits another bob $\mathrm{B}$ of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be
elastic.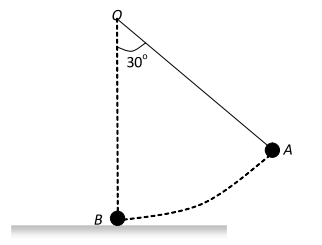 
Ans. The bob A shall not rise. This is because when two bodies of same mass undergo an elastic collision. Their velocities are interchanged after collision ball A will come to rest and the ball B would move with the velocity of A.
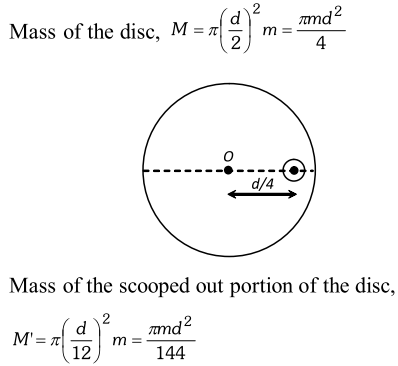
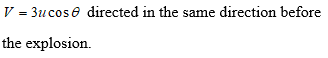
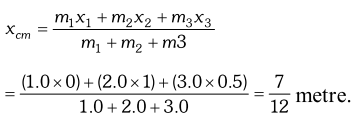
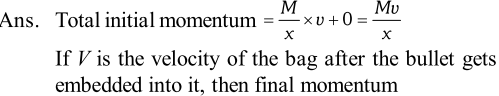
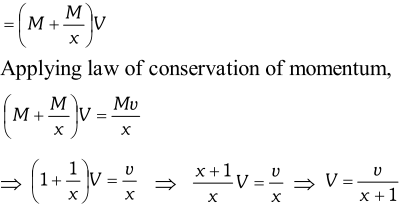
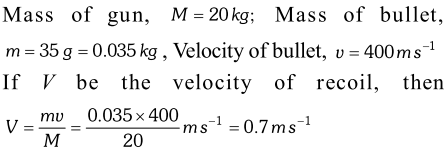
Aliter. Number of bullets fired per second, $n=4$ Momentum given to the bullets per second $=n m v$ Same momentum per second is gained by the gun. This gives the force acting on the gun and also the force applied to keep the gun in position. So, $F=n m v=4 \times 0.035 \times 400 N=56 N$ Aliter. Number of bullets fired per second, $n=4$ Momentum given to the bullets per second $=n m v$ Same momentum per second is gained by the gun. This gives the force acting on the gun and also the force applied to keep the gun in position. So, $F=n m v=4 \times 0.035 \times 400 N=56 N$