A magnetic moment is a quantity that represents the magnetic strength and orientation of a magnet or any other object that produces a magnetic field. More precisely, a magnetic moment refers to a magnetic dipole moment, the component of the magnetic moment that can be represented by a magnetic dipole. Know the Magnetic Dipole Moment Definition, Formulae, and solved examples here.
Ex. The force between two magnetic poles in air is 9.604 mN. If one pole is 10 times stronger than the other, calculate the pole strength of each if distance between two poles is 0.1 m? Sol. Force between poles $F =\frac{\mu_{0}}{4 \pi} \frac{ m _{1} m _{2}}{ r ^{2}}$ or $9.604 \times 10^{-3}=\frac{10^{-7} \times m \times 10 m}{0.1 \times 0.1}$ or $m ^{2}=96.04 N ^{2} T ^{-2}$ or m = 9.8 N/T So strength of other pole is 9.8 × 10 = 98 N/T
Ex. A steel wire of length L has a magnetic moment M. It is then bent into a semicircular arc. What is the new magnetic moment? Sol. If m is the pole strength then M = m . L or $m =\frac{ M }{ L }$ If it is bent into a semicircular arc then L = $\pi$ or $r=\frac{L}{\pi}$ So new magnetic moment $M^{\prime}=m \times 2 r=\frac{M}{L} \times 2 \times \frac{L}{\pi}=\frac{2 M}{\pi}$
Ex. Two identical bar magnets each of length L and pole strength m are placed at right angles to each other with the north pole of one touching the south pole of other. Evaluate the magnetic moment of the system. Sol. $M _{1}= M _{2}= mL$
Sol. $M _{1}= M _{2}= mL$
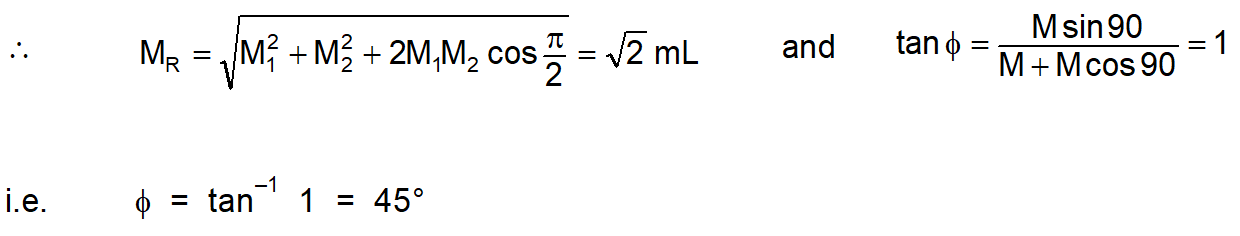
Also Read:
Magnetic Dipole:
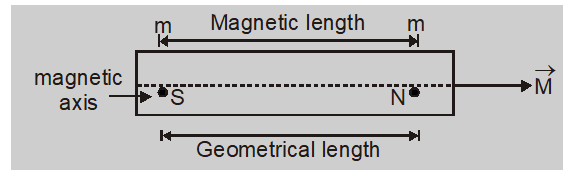
An arrangement of two magnetic poles of equal and opposite strengths separated by a finite distance is called a magnetic dipole.

- Two poles of a magnetic dipole or a magnet are of equal strength and opposite nature.
- The line joining the poles of the magnet is called the magnetic axis.
- The distance between the two poles of a bar magnet is called the magnetic length of the magnet. It is denoted by 2$\ell$
- The distance between the ends of the magnet is called the geometrical length of the magnet.
- The ratio of magnetic length and geometrical length is $\frac{5}{6}$ or 0.83
- A small bar magnet is treated like a magnetic dipole.
Magnetic Dipole Moment Definition:
The product of strength of either pole and the magnetic length of the magnet is called a magnetic dipole moment. $\overrightarrow{ M }= m (\overrightarrow{2 \ell})$Important Points to Remember
-
- It is a vector quantity whose direction is from the south pole to the north pole of a magnet.
- The unit of magnetic dipole moment is ampere metre $^{2}\left( Am ^{2}\right)$ and Joule/Tesla (J/T). The dimensions are $M^{0} L^{2} T^{0} A^{1}$
- If a magnet is cut into two equal parts along the length then pole strength is reduced to half and length remains unchanged.New magnetic dipole moment M' = m' $(2 \ell)=\frac{ m }{2} \times 2 \ell=\frac{ M }{2}$The new magnetic dipole moment of each part becomes half of the original value.

- If a magnet is cut into two equal parts transverse to the length then pole strength remains unchanged and length is reduced tohalf. New magnetic dipole moment $M^{\prime}=m\left(\frac{2 \ell}{2}\right)=\frac{M}{2}$ The new magnetic dipole moment of each part becomes half of the original value.
- In magnetism existence of magnetic monopole is not possible.
- The magnetic dipole moment of a magnet is equal to the product of pole strength and distance between poles. M = m d

- As the magnetic moment is a vector, in the case of two magnets having magnetic moments $M_{1}$ and $M_{2}$ with angle $\theta$ between them, the resulting magnetic moment. $M =\left[ M _{1}^{2}+ M _{2}^{2}+2 M _{1} M _{2} \cos \theta\right]^{1 / 2}$ with $\tan \phi=\left[\frac{M_{2} \sin \theta}{M_{1}+M_{2} \cos \theta}\right]$
Ex. The force between two magnetic poles in air is 9.604 mN. If one pole is 10 times stronger than the other, calculate the pole strength of each if distance between two poles is 0.1 m? Sol. Force between poles $F =\frac{\mu_{0}}{4 \pi} \frac{ m _{1} m _{2}}{ r ^{2}}$ or $9.604 \times 10^{-3}=\frac{10^{-7} \times m \times 10 m}{0.1 \times 0.1}$ or $m ^{2}=96.04 N ^{2} T ^{-2}$ or m = 9.8 N/T So strength of other pole is 9.8 × 10 = 98 N/T
Ex. A steel wire of length L has a magnetic moment M. It is then bent into a semicircular arc. What is the new magnetic moment? Sol. If m is the pole strength then M = m . L or $m =\frac{ M }{ L }$ If it is bent into a semicircular arc then L = $\pi$ or $r=\frac{L}{\pi}$ So new magnetic moment $M^{\prime}=m \times 2 r=\frac{M}{L} \times 2 \times \frac{L}{\pi}=\frac{2 M}{\pi}$
Ex. Two identical bar magnets each of length L and pole strength m are placed at right angles to each other with the north pole of one touching the south pole of other. Evaluate the magnetic moment of the system.
 Sol. $M _{1}= M _{2}= mL$
Sol. $M _{1}= M _{2}= mL$
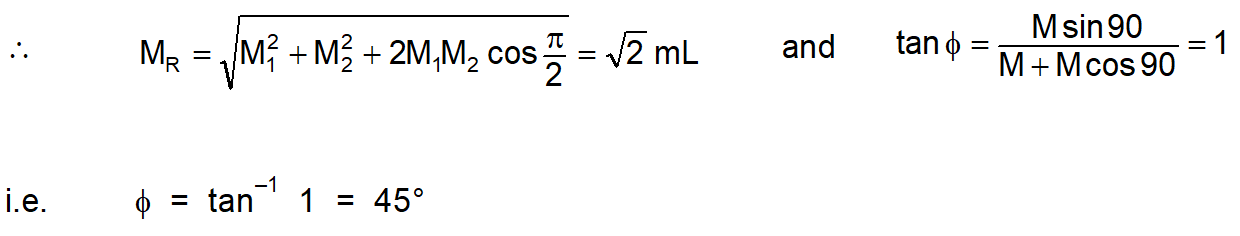
Also Read:
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
