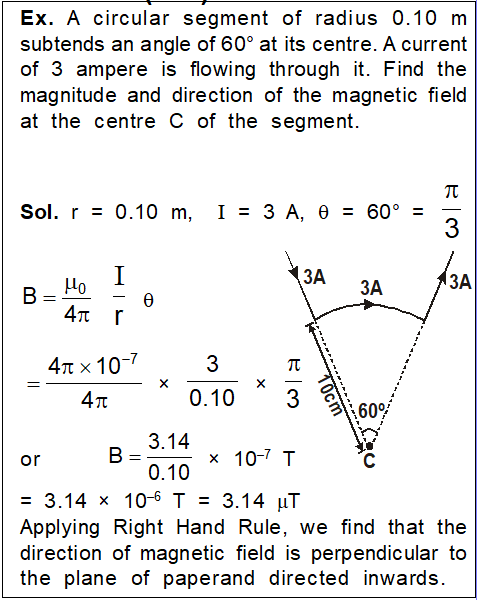
Here we will study about the Magnetic Field at the Centre of a Circular Coil. Here we will study about the number of cases
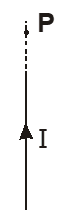
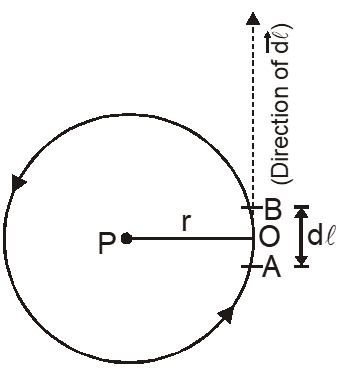
$\mathrm{dB}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{Id} \ell \sin \theta}{r^{2}}$ where $\theta$ is the angle between $\overrightarrow{\mathrm{d} \ell}$ and $\overrightarrow{\mathrm{r}}$.
$\left.\therefore \quad \mathrm{dB}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d \ell \sin 90^{\circ}}{r^{2}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d \ell}{\mathrm{r}^{2}} \quad \text { (for circular loop, } \theta=90^{\circ}\right)$
The loop can be supposed to consists of a number of small elements placed side by side. The magnetic field due to all the elements will be in the same direction. So, the net magnetic field at P is given by
$\mathrm{B}=\sum \mathrm{dB}=\sum \frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} \mathrm{d} \ell}{\mathrm{r}^{2}}=\frac{\mu_{0} \mathrm{I}}{4 \pi \mathrm{r}^{2}} \sum \mathrm{d} \ell$
$\therefore \quad \mathrm{B}=\frac{\mu_{0} \mathrm{I}}{4 \pi r^{2}} \times 2 \pi r$
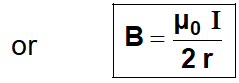 $| \Sigma \mathrm{d} \ell=\text { circumference of the circle }=2 \pi \mathrm{r})$
$| \Sigma \mathrm{d} \ell=\text { circumference of the circle }=2 \pi \mathrm{r})$
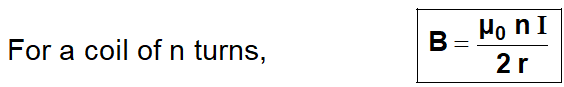

 $B=\frac{\mu_{0} I}{4 \pi r^{2}} \sum d \ell\left(\because \frac{\sum d \ell}{r}=\alpha\right)$
$B=\frac{\mu_{0} I}{4 \pi r^{2}} \sum d \ell\left(\because \frac{\sum d \ell}{r}=\alpha\right)$
$B=\frac{\mu_{0} I}{4 \pi r} \alpha$
Let $x$ be the distance of the observation point $P$ from the centre 0 of the loop. Let us consider an infinitesimally small element $\mathrm{AB}$ of length d\ell. Radius of the loop $=\mathrm{a}$ According to Biot-Savart's law, the magnetic field at P due to this small element
$\begin{aligned} \overrightarrow{\mathrm{dB}} &=\frac{\mu_{0} \mathrm{I}}{4 \pi r^{3}}[\overrightarrow{\mathrm{d}} \ell \times \overrightarrow{\mathrm{r}}] \\ \mathrm{dB} &=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell \sin \theta}{4 \pi \mathrm{r}^{2}} \end{aligned}$
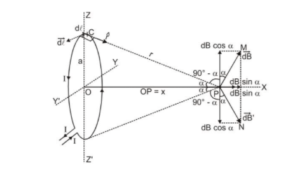 or $\quad \mathrm{dB}=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell}{4 \pi \mathrm{r}^{2}}\left(\theta=90^{\circ}\right)$
or $\quad \mathrm{dB}=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell}{4 \pi \mathrm{r}^{2}}\left(\theta=90^{\circ}\right)$
The direction of $\overrightarrow{\mathrm{dB}}$ is perpendicular to the plane of the current element $\overrightarrow{\mathrm{d} \ell}$ and $\overrightarrow{\mathrm{r}}(\mathrm{CP})$ as shown in fig. by $\overrightarrow{\mathrm{PM}}$
Similarly if we consider another small element just diametrically opposite to this element then
magnetic field due to this at point $P$ is $\overrightarrow{\mathrm{dB}^{\prime}},$ denoted by PN and of the same magnitude. $\mathrm{d} \mathrm{B}=\mathrm{dB}^{\prime}$
Both $\overrightarrow{\mathrm{dB}}$ and $\overrightarrow{\mathrm{dB}^{\prime}}$ can be resolved into two mutually perpendicular components along $\mathrm{PX}$ and $\mathrm{zz}$ :
The components along ZZ' [dB $\cos \alpha$ and $\left.d B^{\prime} \cos \alpha\right]$ cancel each other as they are equal and opposite in direction.
The same will hold for such other pairs of current elements. over the entire circumference of the loop.
Therefore, due to the various current elements, the components of the magnetic field is only along PX will contribute to the magnetic field due to the whole loop at point P.
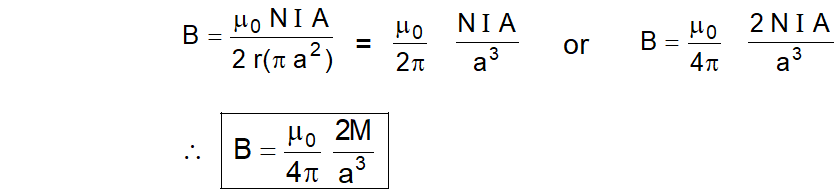
Case II : If the observation point is far far away from the coil, then $a<. So, $a^{2}$ can be neglected in comparison to $x^{2}$.
$\therefore \quad B=\frac{\mu_{0} N I a^{2}}{2 x^{3}}$
terms of magnetic dipole moment, $\mathrm{B}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{x}^{3}} \quad\left[\mathrm{B}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{NIA}}{\mathrm{x}^{3}}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{NIA}}{\mathrm{x}^{3}}\right]$
Also Read: Biot Savart's Law
Click here for the Video tutorials of Magnetic Effect of Current Class 12
- Magnetic Field at the Centre of a Circular Coil
- Magnetic dipole moment of the current loop
Magnetic Field at the Center of a Circular Current-Carrying Coil
Consider a circular coil of radius r through which current I is flowing. Let AB be an infinitesimally small element of length d\ell. According to Biot-Savart's law, the magnetic field dB at the center P of the loop due to this small element d $\ell$ is$\mathrm{dB}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{Id} \ell \sin \theta}{r^{2}}$ where $\theta$ is the angle between $\overrightarrow{\mathrm{d} \ell}$ and $\overrightarrow{\mathrm{r}}$.
$\left.\therefore \quad \mathrm{dB}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d \ell \sin 90^{\circ}}{r^{2}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d \ell}{\mathrm{r}^{2}} \quad \text { (for circular loop, } \theta=90^{\circ}\right)$
The loop can be supposed to consists of a number of small elements placed side by side. The magnetic field due to all the elements will be in the same direction. So, the net magnetic field at P is given by

$\mathrm{B}=\sum \mathrm{dB}=\sum \frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} \mathrm{d} \ell}{\mathrm{r}^{2}}=\frac{\mu_{0} \mathrm{I}}{4 \pi \mathrm{r}^{2}} \sum \mathrm{d} \ell$
$\therefore \quad \mathrm{B}=\frac{\mu_{0} \mathrm{I}}{4 \pi r^{2}} \times 2 \pi r$
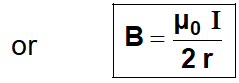 $| \Sigma \mathrm{d} \ell=\text { circumference of the circle }=2 \pi \mathrm{r})$
$| \Sigma \mathrm{d} \ell=\text { circumference of the circle }=2 \pi \mathrm{r})$
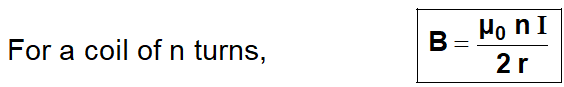
Magnetic Field due to part of the current-carrying circular conductor (Arc) :


 $B=\frac{\mu_{0} I}{4 \pi r^{2}} \sum d \ell\left(\because \frac{\sum d \ell}{r}=\alpha\right)$
$B=\frac{\mu_{0} I}{4 \pi r^{2}} \sum d \ell\left(\because \frac{\sum d \ell}{r}=\alpha\right)$
$B=\frac{\mu_{0} I}{4 \pi r} \alpha$
Magnetic Field on the Axis of a Circular Coil
Consider a circular loop of radius a through which current I is flowing as shown in fig. The point $P$ lies on the axis of the circular current loop i.e., along the line perpendicular to the plane of the loop and passing through its center.Let $x$ be the distance of the observation point $P$ from the centre 0 of the loop. Let us consider an infinitesimally small element $\mathrm{AB}$ of length d\ell. Radius of the loop $=\mathrm{a}$ According to Biot-Savart's law, the magnetic field at P due to this small element
$\begin{aligned} \overrightarrow{\mathrm{dB}} &=\frac{\mu_{0} \mathrm{I}}{4 \pi r^{3}}[\overrightarrow{\mathrm{d}} \ell \times \overrightarrow{\mathrm{r}}] \\ \mathrm{dB} &=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell \sin \theta}{4 \pi \mathrm{r}^{2}} \end{aligned}$
 or $\quad \mathrm{dB}=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell}{4 \pi \mathrm{r}^{2}}\left(\theta=90^{\circ}\right)$
or $\quad \mathrm{dB}=\frac{\mu_{0} \mathrm{I} \mathrm{d} \ell}{4 \pi \mathrm{r}^{2}}\left(\theta=90^{\circ}\right)$
The direction of $\overrightarrow{\mathrm{dB}}$ is perpendicular to the plane of the current element $\overrightarrow{\mathrm{d} \ell}$ and $\overrightarrow{\mathrm{r}}(\mathrm{CP})$ as shown in fig. by $\overrightarrow{\mathrm{PM}}$
Similarly if we consider another small element just diametrically opposite to this element then
magnetic field due to this at point $P$ is $\overrightarrow{\mathrm{dB}^{\prime}},$ denoted by PN and of the same magnitude. $\mathrm{d} \mathrm{B}=\mathrm{dB}^{\prime}$
Both $\overrightarrow{\mathrm{dB}}$ and $\overrightarrow{\mathrm{dB}^{\prime}}$ can be resolved into two mutually perpendicular components along $\mathrm{PX}$ and $\mathrm{zz}$ :
The components along ZZ' [dB $\cos \alpha$ and $\left.d B^{\prime} \cos \alpha\right]$ cancel each other as they are equal and opposite in direction.
The same will hold for such other pairs of current elements. over the entire circumference of the loop.
Therefore, due to the various current elements, the components of the magnetic field is only along PX will contribute to the magnetic field due to the whole loop at point P.
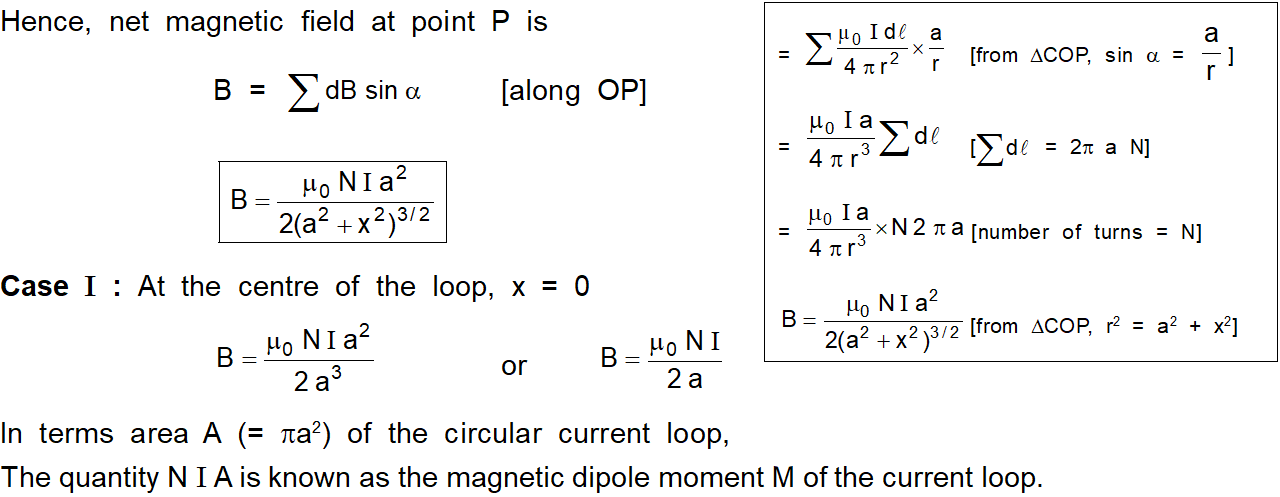

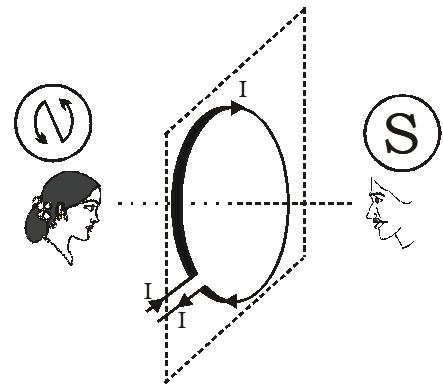
The magnetic dipole moment of the current loop
The current loop can be regarded as a magnetic dipole that produces its magnetic field and the magnetic dipole moment of the current loop is equal to the product of ampere-turns and area of the current loop. we can write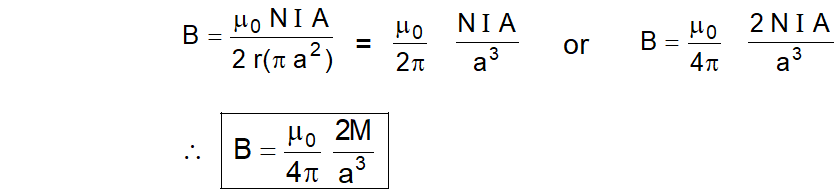
Case II : If the observation point is far far away from the coil, then $a<
$\therefore \quad B=\frac{\mu_{0} N I a^{2}}{2 x^{3}}$
terms of magnetic dipole moment, $\mathrm{B}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{x}^{3}} \quad\left[\mathrm{B}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{NIA}}{\mathrm{x}^{3}}=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{NIA}}{\mathrm{x}^{3}}\right]$
Also Read: Biot Savart's Law
Click here for the Video tutorials of Magnetic Effect of Current Class 12
Comments
Hollie Newman
Dec. 23, 2022, 4:06 p.m.
This is a fantastic article. Thanks for sharing this informative blog. I have become a fan of your blogs, and this blog is so exciting and informative. <a href="https://discountagent.co.uk/blog/" rel="nofollow ugc">Write for us blog</a>
Toby
Dec. 12, 2020, 3:26 a.m.
my site :: coupon list for Emma Mattresses UK here (<a href="http://Gbooks3.melodysoft.com/app?ID=0-post-flowto.free-styl" rel="nofollow ugc">Maximo</a>)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
