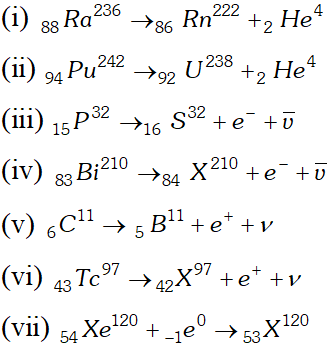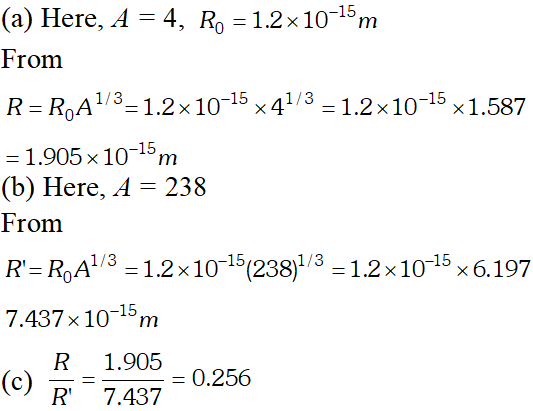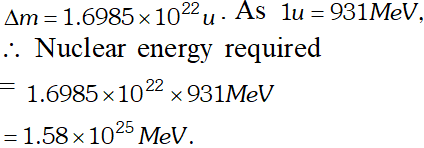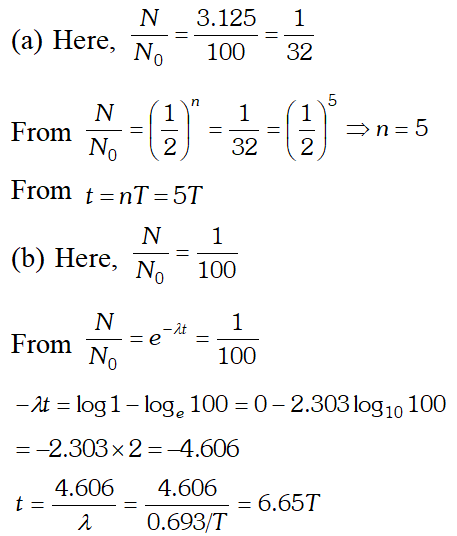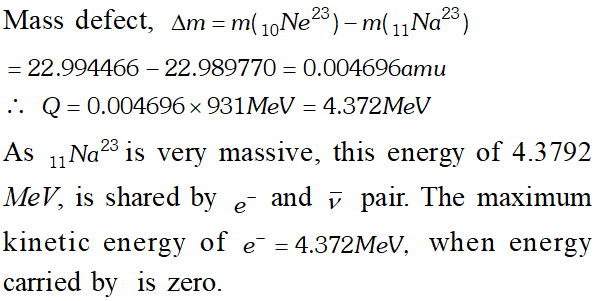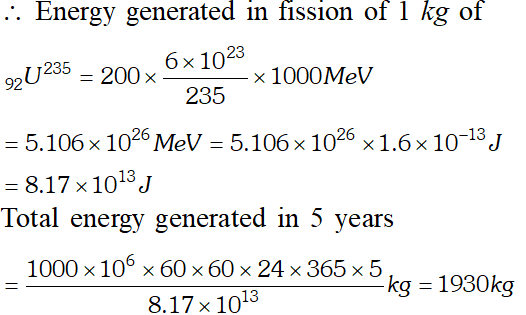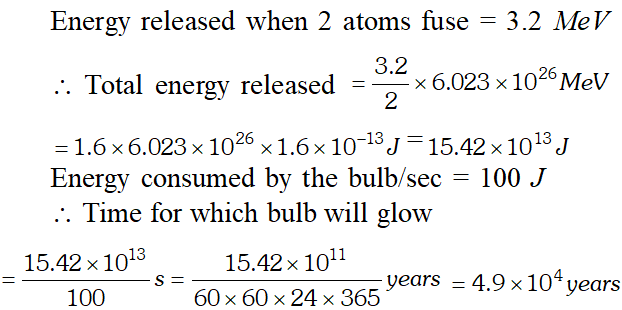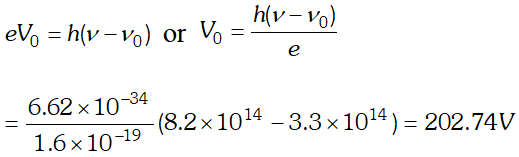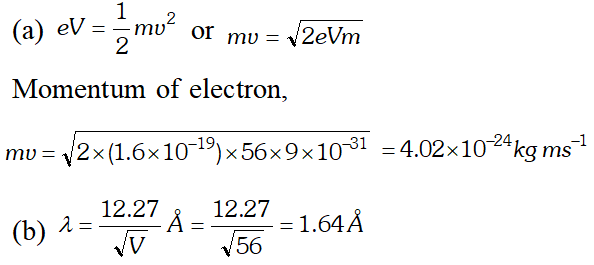Get important questions of Modern Physics Class 12 for Boards exams. Download or View the Physics Question Bank Class 12. These important questions will play significant role in clearing concepts of Physics. This question bank is designed by NCERT keeping in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 12 Physics chapter wise CBSE. Click Here for Detailed Chapter-wise Notes of PHYSICS for Class 12th, JEE & NEET.
Q. Does the stopping potential in photoelectric emission depend upon (i) the intensity of the incident radiation in a photocell ? (ii) The frequency of the incident radiation ?
Ans. (i) No, the stopping potential does not depend upon the intensity of the incident radiation (ii) Yes, the stopping potential depends upon the frequency of the incident radiation.
Q. Show graphically, how the stopping potential for a given photosensitive surface varies with the frequency. Mark threshold frequency on this graph
Ans. 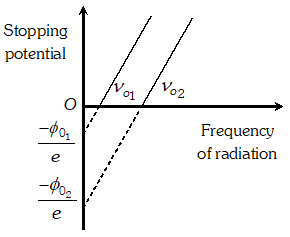
Q. Plot a graph showing the variation of photoelectric current with anode potential for two light beam of same wavelength but different intentisy
Ans. 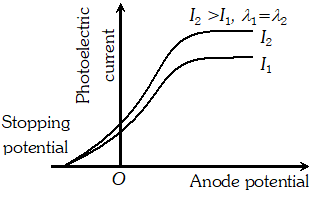
Q. With what purpose was famous Davisson-Germer experiment with the electrons performed ?
Ans. Davisson-Germer experiment established the wave nature of slow moving electrons.
Q. de-Broglie wavelength associated with an electron accelerated through a potential difference V is $\lambda$. What will be it’s wavelength when the accelerating potential is increased to 4 V ?
Ans. de-Broglie wavelength $\lambda \propto \frac{1}{\sqrt{V}}$
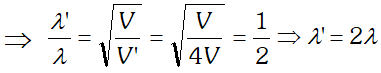
Q. In an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be $4.12 \times 10^{-15} \mathrm{Vs}$ Given $e=1.6 \times 10^{-19} \mathrm{C}$ estimate the value of Planck’s constant. [NCERT]
Ans. 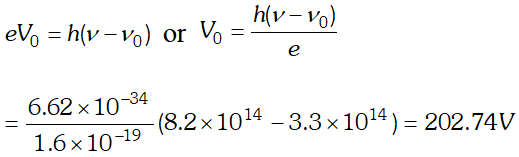
Q. The threshold frequency of a certain metal is $3.3 \times 10^{14} \mathrm{Hz}$ If light of frequency $8.2 \times 10^{14} \mathrm{Hz}$, is incident on the metal, predict the cut off voltage for photoelectric emission. Given plank’s constant $h=6.62 \times 10^{-34} \mathrm{J}$ [NCERT]
Ans. 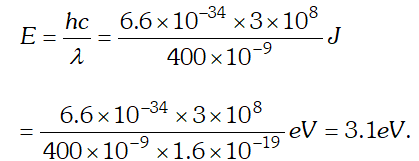
Q. The threshold frequency of a metal is f0. When the light of frequency 2f0 is incident on the metal plate the maximum velocity of electrons emitted is v1. When the frequency of the incident radiation is increased to 5f0, the maximum velocity of electrons emitted is v2. Find the ratio of v1 and v2.
Ans.By using $E=W_{0}+K_{\max } \Rightarrow K_{\max }=E-W_{0}$ Where 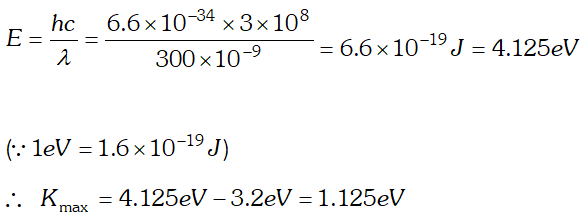
Q. Given below is the graph between frequency () of the incident light and maximum kinetic energy(Ek) of emitted photoelectrons. Find the values of (i). Threshold frequency, and (ii) Work function from the graph
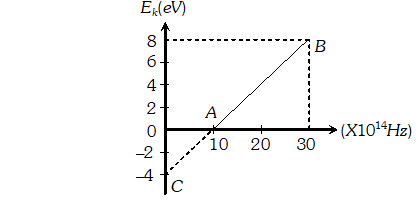
Ans. 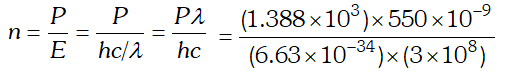 $=3.84 \times 10^{21}$ photons/m'-s
$=3.84 \times 10^{21}$ photons/m'-s Q. The energy flux of sunlight reaching the surface of the earth is $1.388 \times 10^{3} \mathrm{W} / \mathrm{m}^{2}$. How many photons (nearly) per square metre are incident on the earth per second ? Assume that the photons in the sunlight have an average wavelength of 550 nm [NCERT]
Ans. 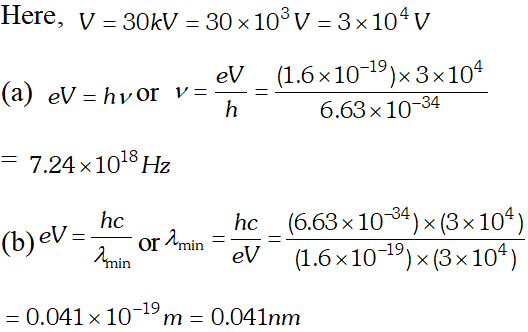
Q. Find the (a) maximum frequency and (b) minimum wave length of X-rays produced by 30 kV electrons [NCERT]
Ans. (a) maximum kinetic energy
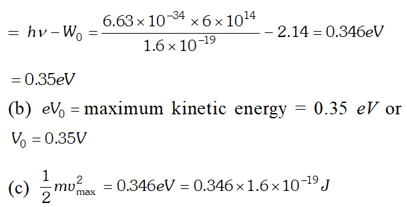
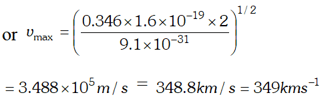
Q. The work function of cesium metal is 2.14 eV. When light of frequency $6 \times 10^{14} \mathrm{Hz}$ is incident on the metal surface, photoemission of electrons occurs. What is the (a) maximum kinetic energy of the emitted electrons (b) Stopping potential and (c) Maximum speed of the emitted photoelectrons. Given $h=6.63 \times 10^{-34} \mathrm{Js}, \quad 1 e V=1.6 \times 10^{-19} \mathrm{J}, \mathrm{c}=3 \times 10^{8} \mathrm{m} / \mathrm{s}$ , [NCERT]
Ans. 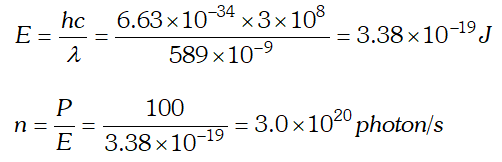
Q. A 100 W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm. (a) What is energy associated per photon with the sodium light (b) At what rate are the photons delivered to the sphere ? [NCERT]
Ans. 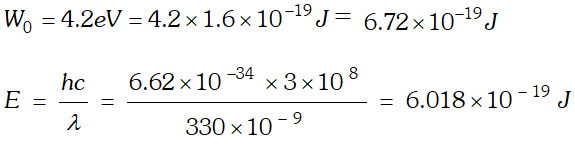 As energy of incident photon $E
As energy of incident photon $E Q. The work unction for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm? Given, charge on electron, $e=1.6 \times 10^{-19} \mathrm{C}, \quad c=3 \times 10^{8} \mathrm{m} / \mathrm{s} ; h=6.62 \times 10^{-34} \mathrm{Js}$
Ans. 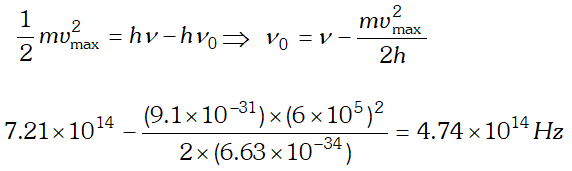
Q. Light of frequency $7.21 \times 10^{14} \mathrm{Hz}$ is incident on a metal surface. Electrons with a maximum speed of $6.0 \times 10^{5} \mathrm{ms}^{-1}$ are ejected from the surface. What is the threshold frequency for photoemission of electrons ? $h=6.63 \times 10^{-34} \mathrm{Js}$ and $m_{e}=9.1 \times 10^{-31} \mathrm{kg}$ [NCERT]
Ans. Using $E=W_{0}+e V_{0} \Rightarrow V_{0}=\frac{E}{e}-\frac{W_{0}}{e}=\frac{h c}{e \lambda}-\frac{W_{0}}{e}$ $=\frac{\left(6.63 \times 10^{-34}\right) \times 3 \times 10^{8}}{\left(488 \times 10^{-9}\right) \times 1.6 \times 10^{-19}}-0.38=2.17 e V$
Q. Light of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the cathode, the stopping potential of photoelectrons is 0.38 eV. Find the work function of the material from which the cathode is made. Given $h=6.63 \times 10^{-34} \mathrm{Js}, 1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{J}$ [NCERT]
Ans. 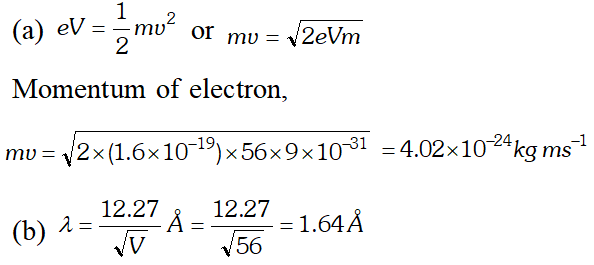
Q. Calculate the (a) momentum and (b) de-Broglie wavelength of the electrons accelerated through a potential difference of 56 V. Given; $h=6.63 \times 10^{-34} \mathrm{Js}, m_{e}=9 \times 10^{-31} \mathrm{kg}$ ;
Ans. 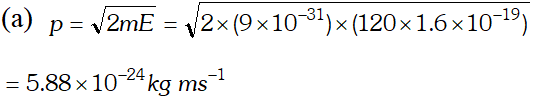
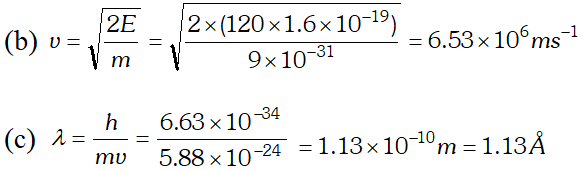
Q. The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which (a) an electron (b) a neutron, would have the same de-Broglie wavelength $h=6.6 \times 10^{-34} \mathrm{Js}, m_{e}=9 \times 10^{-31} \mathrm{kg} ; m_{n}=1.66 \times 10^{-27} \mathrm{kg}$ [NCERT]
Ans. (a) From electron or photon, momentum $p=\frac{h}{\lambda}$
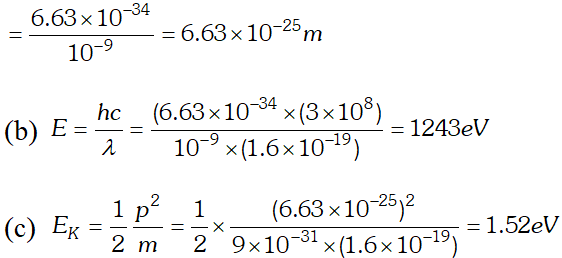
Ans. 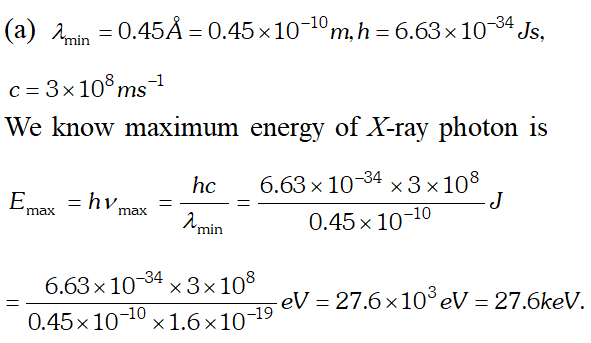 (b) In X-ray tube, accelerating voltage provides the energy to the electrons which on striking the anti-cathode, produce X-ray for getting X-ray photons of 27.6 keV, it is required that the incident electrons must possess kinetic energy of at least 27.6 keV. Therefore accelerating voltage of the order of 30 keV should be applied across the X-ray tube to get the required X-ray photons.
(b) In X-ray tube, accelerating voltage provides the energy to the electrons which on striking the anti-cathode, produce X-ray for getting X-ray photons of 27.6 keV, it is required that the incident electrons must possess kinetic energy of at least 27.6 keV. Therefore accelerating voltage of the order of 30 keV should be applied across the X-ray tube to get the required X-ray photons. Q. (a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at $0.45 \mathrm{A}$ What is the maximum energy of a photon in the radiation ? (b) From answer to (a), give what order of accelerating voltage (for electrons) is required in such a tube. [NCERT]
Ans. Using Einstein photoelectric equation $E=W_{0}+K_{\max }$
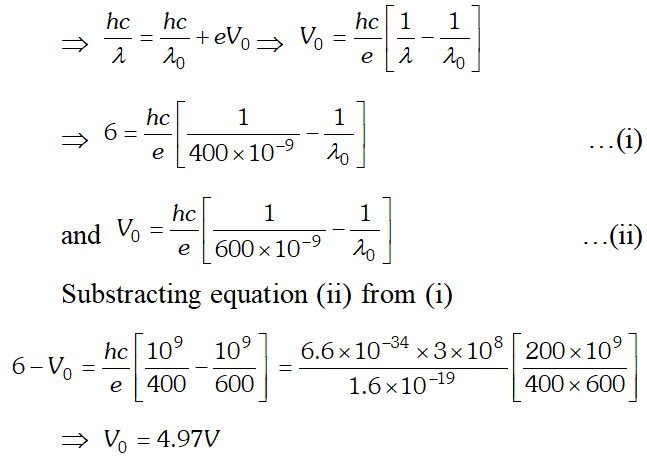
Q. An electron and a proton are possessing same amount of kinetic energy which of the two have greater de-Broglie wavelength ? Justify your answer
Ans. Kinetic energy of electron, $E=\frac{1}{2} m_{1} v_{1}^{2}$ or $m_{1} v_{1}=\sqrt{2 E m_{1}}$ $\therefore$ De-Broglie wavelength associated with moving Electron $\lambda_{1}=\frac{h}{m_{1} v_{1}}=\frac{h}{\sqrt{2 E m_{1}}}$ …(i) Kinetic energy of proton, $E=\frac{1}{2} m_{2} v_{2}^{2}$ or $m_{2} v_{2}=\sqrt{2 E m_{2}}$ $\therefore$ De-Broglie wavelength associated with proton, $\lambda_{2}=\frac{h}{m_{2} v_{2}}=\frac{h}{\sqrt{2 E m_{2}}}$ …(ii) $\frac{\lambda_{1}}{\lambda_{2}}=\sqrt{\frac{m_{2}}{m_{1}}}>1$ or $\lambda_{1}>\lambda_{2} |$ De-Broglie wavelength associated with electron is greater than that of proton.
Q. Define the terms (i) work function (ii) threshold frequency and (iii) stopping potential, with reference to photoelectric effect
Ans. (i) Work function of a metal is the minimum energy required by an electron to just escape from the metal surface so as to overcome the restraining forces at the surface. (ii) Threshold frequency is the minimum frequency fo the incident radiation for which the photoelectrons are just emitted from a metal surface without any kinetic energy. (iii) Stopping potential or cut off potential is that minimum negative potential given to anode in a photo-cell for which the photoelectric current becomes zero.
Q. X-rays of wavelength $\lambda$ fall on a photosensitive surface, emitting photoelectrons. Assuming X-rays of wavelength $\lambda$ fall on a photosensitive surface, emitting electrons. Assuming that the work function of the surface can be neglected, prove that the de- Broglie wavelength of electrons emitted will be $\sqrt{\frac{h \lambda}{2 m c}}$
Ans. Given $\phi_{0}=0$ Using Einstein’s photoelectric equation, we have
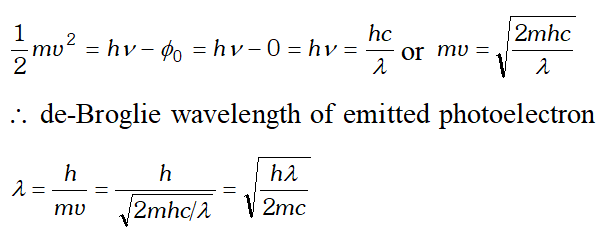
Q. The wavelength of a photon and the de-Broglie wavelength of an electron have the same value. Show that the energy of the photon is $\frac{2 \lambda m c}{h}$ times the kinetic energy of the electron, where m, c and h have their usual meanings.
Ans. Kinetic energy of electron, $E_{K}=\frac{1}{2} \frac{m^{2} v^{2}}{m}=\frac{1}{2} \frac{h^{2}}{m \lambda 2}$ $\left[\because \lambda=\frac{h}{m v}\right]$
Energy of a photon, $E=\frac{h c}{\lambda}$ 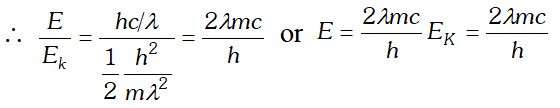
Q. Quarks inside protons and neutrons are thought to carry fractional charges Why do they not show up in Milikan’s oil drop experiment ? [NCERT]
Ans. The quarks having fractional charges are thought to be confined within a proton and a neutron. These quarks are bound by forces. These forces become stronger when the quarks are tried to be pulled apart. That is why, the quarks always remain together. It is due to this reason that though fractional charges does exist in nature but the observable charges are always integral multiple of charge of electron.
Q. Sketch the graphs, showing the variation of stopping potential with frequency of incident radiations for two photosensitive materials A and B having threshold frequencies $v_{0}>v_{0}$respectively. (i) Which of the two metals, A or B has higher work function ? (ii) Which in formation do you get from the slope of the graphs ? (ii) What does the value of the intercept of graph A on the potential axis represent ?
Ans. (i) Metal A has a higher work function because $v_{0}^{\prime}>v_{0}$ (ii) Slope of $V_{0}-\nu$ graph is $\frac{h}{e}$ where $h=$ Plank's constant and $e=$ electronic charge (iii) Intercept of graph $A$ on the potential axis $=\frac{-W_{0}^{\prime}}{e}=-\frac{h \nu_{0}}{e}$
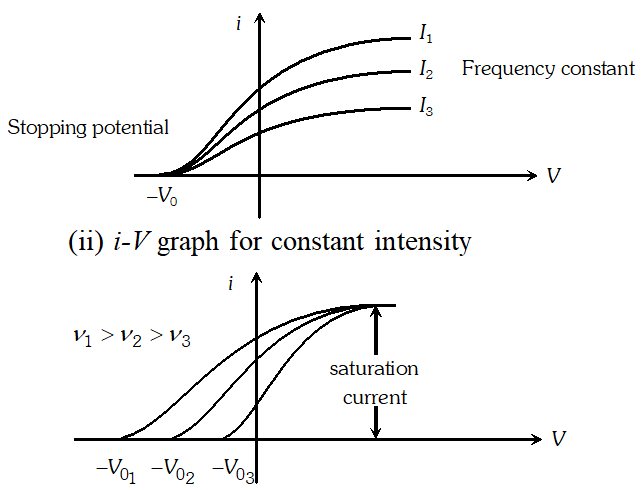
Q. Draw the graphs showing the variation of photoelectric current with anode potential of a photocell for (i) The same frequencies but different intensities $I_{1}>I_{2}>I_{3}$ of incident radiations (ii) The same intensity but different frequencies $v_{1}>v_{2}>v_{3}$ of incident radiations
Ans. (i) i-V graph for same frequency
Q. What is the de-Broglie wavelength of (a) a bullet of mass 0.40 kg travelling at a speed of $1.0 \mathrm{kms}^{-1}$ (b) a ball of mass 0.60 kg moving at a speed of 1.0 $m s^{-1}$ and (c) a dust particle of mass $1.0 \times 10^{-9} \mathrm{kg}$ drifting with a speed of $2.2 \mathrm{ms}^{-1} ? h=6.63 \times 10^{-34} \mathrm{J} \mathrm{s}$ [NCERT]
Ans. 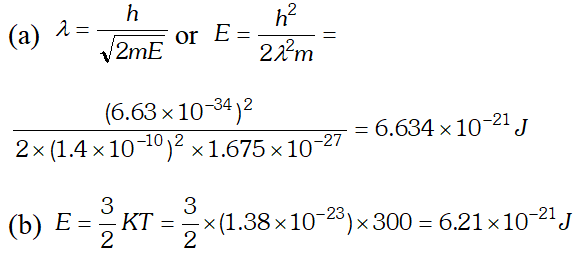
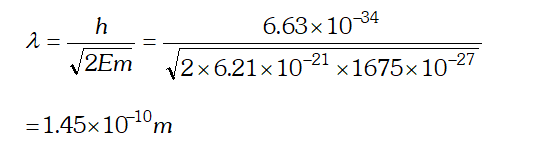
Q. (a) For what kinetic energy of a neutron will the associated de-Broglie wavelength be (b) Also find the de-Broglie wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of $\frac{3}{2} k T$ at 300 K. Given $h=6.63 \times 10^{-34} \mathrm{Js}, m_{n}=1.675 \times 10^{-27} \mathrm{kg}$ $k=1.38 \times 10^{-23} \mathrm{JK}^{-1}$ [NCERT]
Ans. 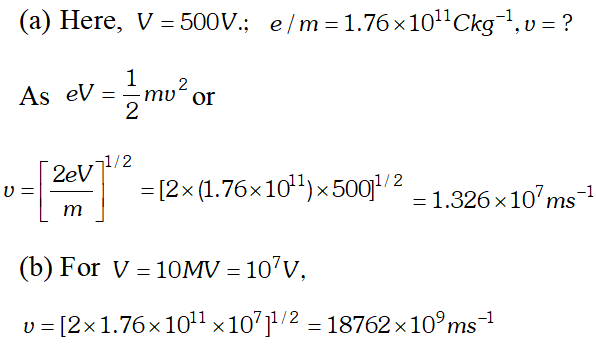 As this speed is greater than the speed of light, so this speed is not possible because as v approaches c, mass of electron becomes infinite $\left[\because m=\frac{m_{0}}{\sqrt{1-v^{2} / C^{2}}}\right]$ so the formula has to be modified.
As this speed is greater than the speed of light, so this speed is not possible because as v approaches c, mass of electron becomes infinite $\left[\because m=\frac{m_{0}}{\sqrt{1-v^{2} / C^{2}}}\right]$ so the formula has to be modified. Q. The work function for the following metals is given $\therefore \quad \mathrm{Na}: 2.75 \mathrm{eV} ; \quad K: 2.30 \mathrm{eV} ; \mathrm{MO}: 4.17 \mathrm{eV} ; \mathrm{Ni}: 5.15 \mathrm{eV}$ Which of these metals will not given photoelectric emission for a radiation of wavelength 3300 Å from a He-Cd laser placed 1 m away from the photocell ? What happens if the laser is brought nearer and placed 50 cm away? [NCERT]
Ans. 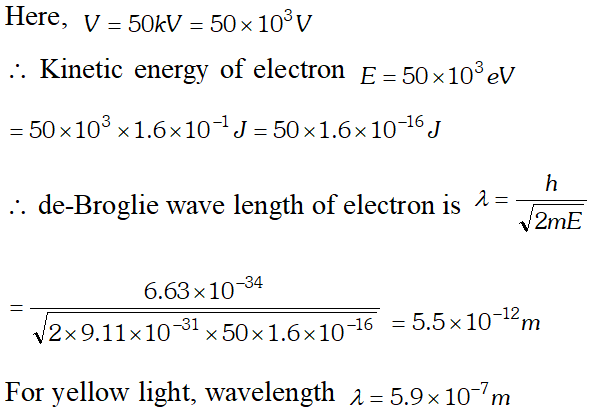
Since resolving power (R.P.) is inversely proportional to wave length, therefore R.P. of an electron microscope is about $10^{5}$ times that of an optical microscope. In practice, differences in other (geometrical) factors can change their comparison somewhat.
Q. In an accelerator experiment on high energy collisions of electrons with positrons, a certain event is interpreted as annihilation of an electron-positron pair of total energy 10.2 BeV into two $\gamma$ -rays of equal energy. What is the wavelength associated with each $\gamma$ -ray $?\left(1 B e V=10^{9} e V\right)$ ? [NCERT]
Ans. 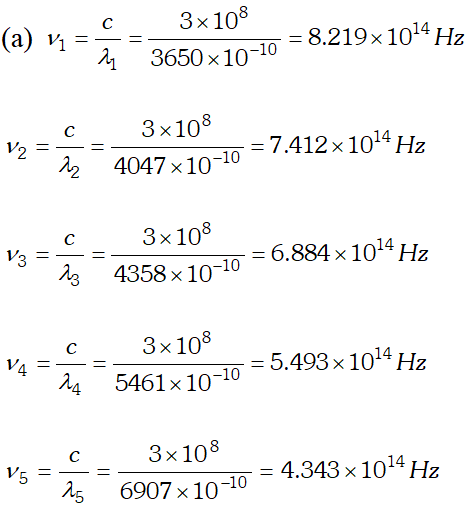 We know that, $e V_{0}=h v-W_{0}$ $\Rightarrow V_{0}=\frac{h v}{e}-\frac{W_{0}}{e}$ Hence a graph between frequency and stopping potential $V_{0}$, must be a straight line. On plotting a graph between given frequencies and corresponding values of stopping potentials we get a straight line with first four points. This straight line is cutting v-axis at $5.0 \times 10^{14} \mathrm{Hz}$ The fifth point comes in the range of $v
We know that, $e V_{0}=h v-W_{0}$ $\Rightarrow V_{0}=\frac{h v}{e}-\frac{W_{0}}{e}$ Hence a graph between frequency and stopping potential $V_{0}$, must be a straight line. On plotting a graph between given frequencies and corresponding values of stopping potentials we get a straight line with first four points. This straight line is cutting v-axis at $5.0 \times 10^{14} \mathrm{Hz}$ The fifth point comes in the range of $v 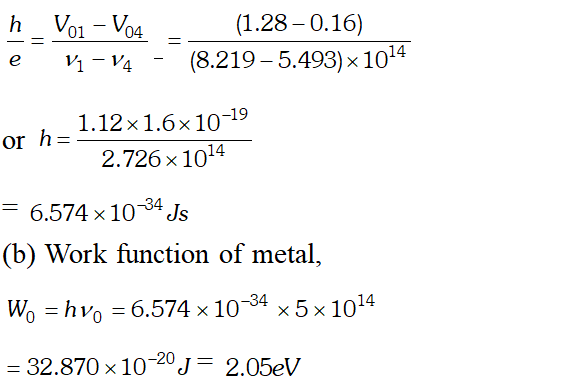
Q. How can de-Broglie wave hypothesis be verified experimentally or Describe Davission and Germer experiment to establish the wave nature of electrons.
Ans. It consists of an electron gun which comprises of a tungsten filament F, coated with barium oxide and heated by a low voltage power supply (L.T. or battery). Electrons emitted by the filament are accelerated to a desired velocity.
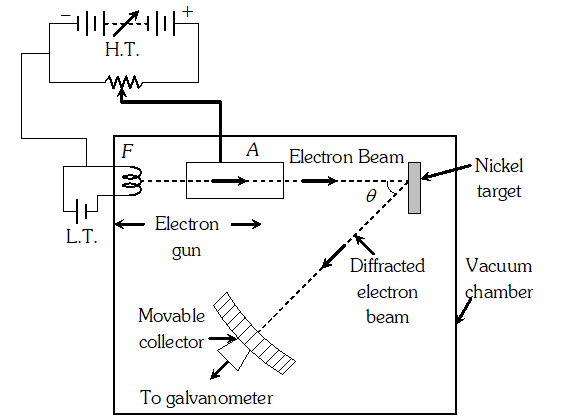 By applying suitable voltage from a high voltage power supply (H.T. or battery), they are made to pass through a cylinder with fine holes along its axis, producing a fine collimated beam. The beam is made to fall on the surface of a nickel crystal. The electrons are scattered in all directions by the atoms of the crystal. The intensity of the electron beam, scattered in a given direction, is measured by the electron detector (collector). The detector can be moved on a circular scale and is connected to a sensitive galvanometer, which records the current. The deflection of the galvanometer is proportional to the intensity of the electron beam entering the collector. The apparatus is enclosed in an evacuated chamber. By moving the detector on the circular scale at different positions, the intensity of the scattered electron beam is measured for different values of an angle of scattering $\theta$ which is the angle between the incident and the scattered electron beams. The variation of intensity (I) of the scattered electrons with the angle of scattering $\theta$ is obtained for different accelerating voltages. The experiment was performed by varying the accelerating voltage from 44 V to 68 V. It was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle $\theta=50^{\circ}$ From the electron diffraction measurements the wavelength of matter waves was found to be 0.165 nm. The de-Broglie wavelength $\lambda$ associated with electrons using equation for is given by $\lambda=h / p=\frac{12.27}{\sqrt{V}}=n m \Rightarrow \lambda=\frac{1.22}{\sqrt{54}} n m=0.167 n m$ Davisson Germer experiment thus strikingly confirms the wave nature of electrons and the de-Broglie relation
By applying suitable voltage from a high voltage power supply (H.T. or battery), they are made to pass through a cylinder with fine holes along its axis, producing a fine collimated beam. The beam is made to fall on the surface of a nickel crystal. The electrons are scattered in all directions by the atoms of the crystal. The intensity of the electron beam, scattered in a given direction, is measured by the electron detector (collector). The detector can be moved on a circular scale and is connected to a sensitive galvanometer, which records the current. The deflection of the galvanometer is proportional to the intensity of the electron beam entering the collector. The apparatus is enclosed in an evacuated chamber. By moving the detector on the circular scale at different positions, the intensity of the scattered electron beam is measured for different values of an angle of scattering $\theta$ which is the angle between the incident and the scattered electron beams. The variation of intensity (I) of the scattered electrons with the angle of scattering $\theta$ is obtained for different accelerating voltages. The experiment was performed by varying the accelerating voltage from 44 V to 68 V. It was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle $\theta=50^{\circ}$ From the electron diffraction measurements the wavelength of matter waves was found to be 0.165 nm. The de-Broglie wavelength $\lambda$ associated with electrons using equation for is given by $\lambda=h / p=\frac{12.27}{\sqrt{V}}=n m \Rightarrow \lambda=\frac{1.22}{\sqrt{54}} n m=0.167 n m$ Davisson Germer experiment thus strikingly confirms the wave nature of electrons and the de-Broglie relation Q. The value of ground state energy of hydrogen atom is –13.6 eV (i) What does the negative sign signify ? (ii) How much energy is required to take an electron in this atom from the ground state to the first excited state
Ans. (i) The negative sign shows that the electron is bound to the nucleus by means of electrostatic attraction. (ii) Energy in ground state $E_{i}=-13.6 e V$ Energy in first excited state $E_{f}=\frac{-13.6}{n^{2}}=\frac{-13.6}{(2)^{2}}=-3.4 e V$ $E=E_{f}-E_{i}=-3.4-(-13.6)=+10.2 e V$
Q. The energy of an electron in an excited hydrogen atom is –3.4 eV. Calculate the angular momentum of the electron according to Bohr’s theory. Plank’s constant $h=6.6 \times 10^{-34} \mathrm{J} \times \mathrm{sec}$
Ans. $E=\frac{-13.6}{n^{2}}=-3.4 \Rightarrow n=2$ $\therefore$ Angular momentum of electron $=\frac{n h}{2 \pi}=\frac{2 h}{2 \pi}=\frac{h}{\pi}$
Q. The electron in the hydrogen atom passes from the n=4 energy level to the n=1 level. What is the maximum number of photons that can be emitted? and minimum number?
Ans. Maximum number of photons is $6,$ corresponding
to transitions $4 \rightarrow 3,3 \rightarrow 2,2 \rightarrow 1,4 \rightarrow 2,3 \rightarrow 1,4 \rightarrow 1$ 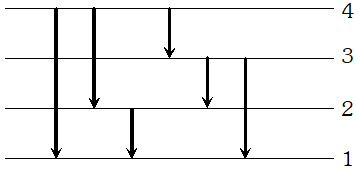 The minimum number of photons can be one only corresponding to the transition $4 \rightarrow 1$
The minimum number of photons can be one only corresponding to the transition $4 \rightarrow 1$ Q. Which state of the triply ionised beryllium $\left(B e^{+++}\right)$ has the same orbital radius as that of the ground state of hydrogen? compare the energies of the two states? [NCERT]
Ans. 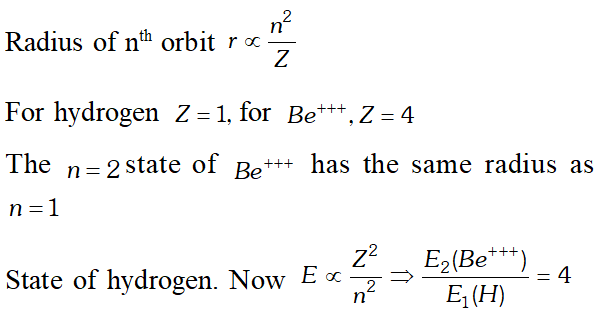
Q. 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom transits from the upper level to the lower level [NCERT]
Ans. 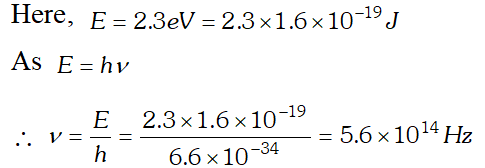
Q. Ground state energy of hydrogen atom is –13.6 eV. What are the kinetic and potential energies of the electron in this state [NCERT]
Ans. Total energy, , $E=-13.6 e V$
Kinetic energy $=-E=13.6 e V$ 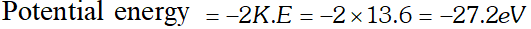
Q. The radius of innermost electron orbit of a hydrogen atom is $5.3 \times 10^{-11} \mathrm{m}$. What are the radii of and orbits ? [NCERT]
Ans. 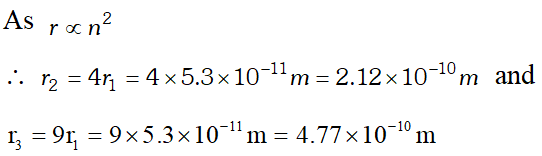
Q. The ground state energy of hydrogen atom is If an electron makes a transition from an energy level –0.85 eV to –3.4 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum, does this wavelength belong
Ans. Energy of emitted photon
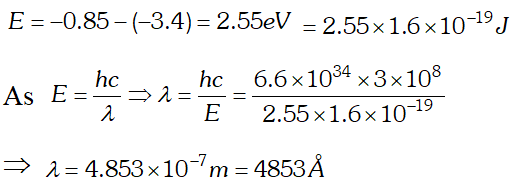 This wavelength belongs to Balmer series of hydrogen spectrum.
This wavelength belongs to Balmer series of hydrogen spectrum. Q. What is the shortest wavelength present in the Paschen series of spectral lines. [NCERT]
Ans. From Rydberg’s formula
$\frac{h c}{\lambda}=13.6 \times 1.6 \times 10^{-19}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]$ For shortest wavelength in Paschen series $n_{2}=\infty$ and $n_{1}=3$ 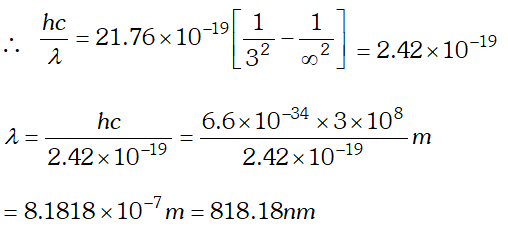
Q. The total energy of electron in the first excited state of hydrogen atom is about –3.4 eV. (a) What is kinetic energy of electron in this state (b) What is potential energy of electron in this state (c) Which of the answers above would change if the choice of zero of potential energy is changed [NCERT]
Ans. We know kinetic energy of electron $=\frac{K Z e^{2}}{2 r}$ and $\mathrm{P.E}$ of electron $=-\frac{K Z e^{2}}{r}$ P.E. = – 2 (kinetic energy) In this calculation electric potential and hence potential energy is zero at infinity. Total energy $=\mathrm{P.E.}+\mathrm{K.E.}=-2 \mathrm{K.E.}+\mathrm{K.E.}=-$ $\mathrm{K.E.}$ (a) In the first excited state, total energy $=-3.4$ eV $\therefore \mathrm{K.E.}=-(-3.4 \mathrm{eV})=+3.4 \mathrm{eV}$ (b) P.E. of electron in this first excited state $=-2 K E=-2 \times 3.4=-6.8 e V$ (c) If zero of potential energy is changed, KE does not change and continues to be + 3.4 eV. However, the P.E. and total energy of the state would change with the choice of zero of potential energy.
Q. From the relation $R=R_{0} A^{1 / 3}$ where is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A). [NCERT]
Ans. Density of nuclear matter $=\frac{\text { mass of nucleus }}{\text { volume of nucleus }}$
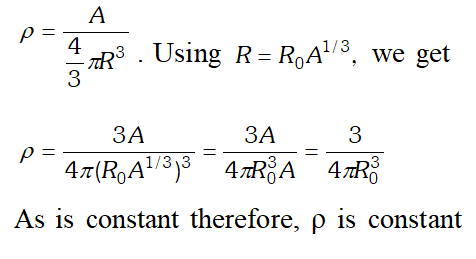
Q. Draw a graph showing the variation of binding energy per nucleon with mass number of different nuclei. Mark the region where the nuclei are most stable. Give the reason for the decrease of binding per nucleon for nuclei with high mass numbers.
Ans. Their exist peaks in the curve corresponding to mass number . The nuclei corresponding to these mass number have more binding energy per nucleon than their immediate neighbours. So they are most stable nuclei.
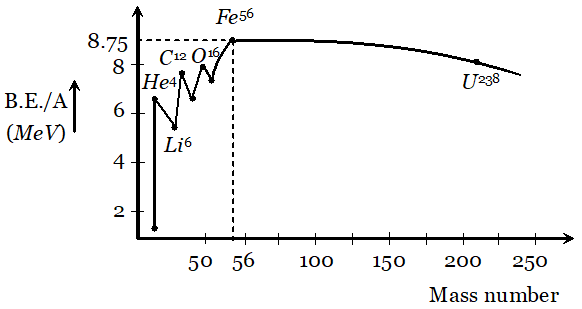 From the curve it is clear that binding energy per nucleon is maximum for iron $\left(_{26} F e^{56}\right)$ having mass number 56, so it is most stable. The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.
From the curve it is clear that binding energy per nucleon is maximum for iron $\left(_{26} F e^{56}\right)$ having mass number 56, so it is most stable. The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei. Q. Derive the relationship between decay constant $(\lambda)$ and half life time $\left(T_{1 / 2}\right)$ of a radioactive sample
Ans. By using $N=N_{0} e^{-\lambda t}$. where $N=$ number of
undecayed atom at time $t, N_{0}=$ number of atoms present at time $t=0$ and $\lambda=$ decay constant. If $t=T_{1 / 2}$ then $N=N_{0}$ 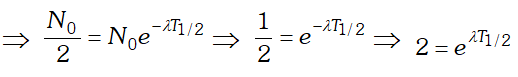 Taking loge both the sides we get
Taking loge both the sides we get 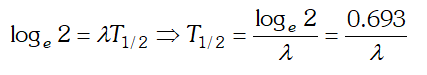 This is the required relation
This is the required relation Q. Draw a graph showing the variation of potential energy of a pair of nucleons as a function of their separation. Indicate the regions in which nuclear force is (i) Attractive (ii) Repulsive
Ans. 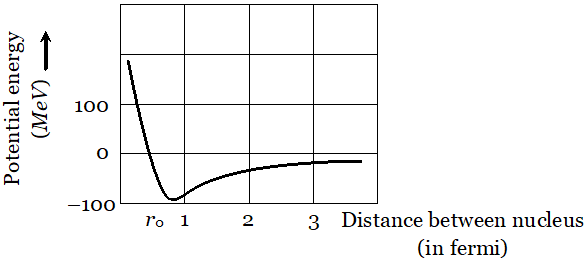 The potential energy is minimum at a distance $r_{0} \approx 0.8 \mathrm{fm}$ This means that the force is attractive for distances larger than 0.8 fm and repulsive if nucleons separated by distance less than 0.8 fm.
The potential energy is minimum at a distance $r_{0} \approx 0.8 \mathrm{fm}$ This means that the force is attractive for distances larger than 0.8 fm and repulsive if nucleons separated by distance less than 0.8 fm. Q. Show that the decay rate ‘R’ of a sample of a radionuclide is related to the number of radioactive nuclei ‘N’ at the same instant by the expression $R=\lambda N$
Ans. Rate of disintegration of a radioactive sample, $R=-\frac{d N}{d t} .$ According to radioactive decay $\operatorname{law}_{2}-\frac{d N}{d t} \propto N \Rightarrow-\frac{d N}{d t}=\lambda N,$ hence $R=\lambda N$
Q. Write nuclear reaction equations for $[\mathrm{NCERTI}]$ (i) $\alpha$ decay of $\mathrm{Ra}^{226} \quad$ (iii) $\alpha$ decay of $_{94} P u^{242}$ (iii) $\beta^{-}$ decay of $_{15} P^{32} \quad$ (iv) $\beta^{-}$ decay of $_{83} B i^{210}$ (v) $\beta^{+}$ decay of $_{6}^{15} C^{11} \quad$ (vi) $\beta^{+}$ decay of $_{43} T c^{97}$ (vii) Electron capture of $_{54} X e^{120}$
Ans. 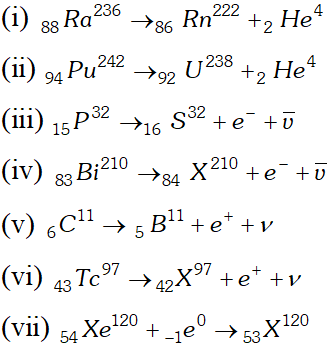
Q. Obtain the approximate value of the radius of (a) a nucleus of $2^{H e^{4}}$ and (b) a nucleus of $g U^{288}(\mathrm{c})$ What is the ratio of these radii? Assume $R_{0}=1.2 \times 10^{-15} \mathrm{m}$ [NCERT]
Ans. 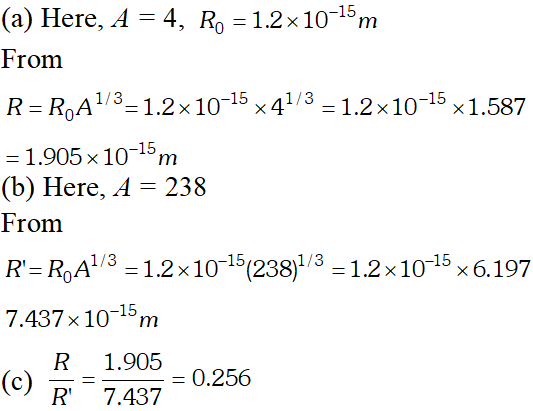
Q. A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity, assume that the coin is entirely made of $_{29} C u^{63}$ atoms (of mass 62.92960 u). The masses of proton and neutron are 1.00783 u and 1.00867 u respectively [NCERT]
Ans. Number of atoms in 3 g coin
$=\frac{6.023 \times 10^{23} \times 3}{63}=2.868 \times 10^{22}$ Each atom of copper contains 29 protons and 34 neutrons. Therefore mass defect of each atom $=[29 \times 1.00783+34 \times 1.00867]-62.92960=0.59225 u$ Total mass defect for all the atoms $=0.59225 \times 2.868 \times 10^{22} u$ 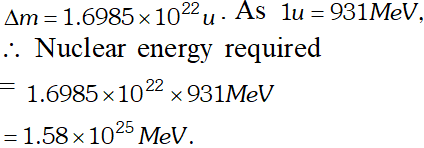
Q. A radioactive isotope has a half life of T years. After how much time is its activity reduced to (a) 3.125% (b) 1% of its original activity? [NCERT]
Ans. 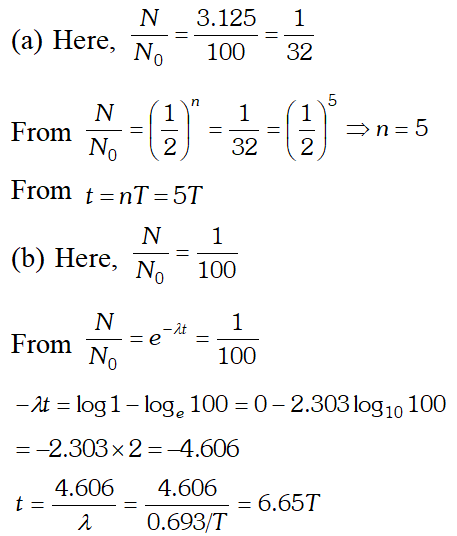
Q. The nucleus $_{10} N e^{23}$ decays by $\beta^{-}$ emission. Write down the decay equation and determine the maximum kinetic energy of the electrons emitted from the following data [NCERT]
Ans. The $B^{-}$ decay of $_{10} N e^{23}$ may be represented as $_{10} N e^{23} \rightarrow_{11} N a^{23}+_{-1} e^{0}+\bar{v}+Q$ Ignoring the rest mass of antineutrino $(\bar{v})$ and electron 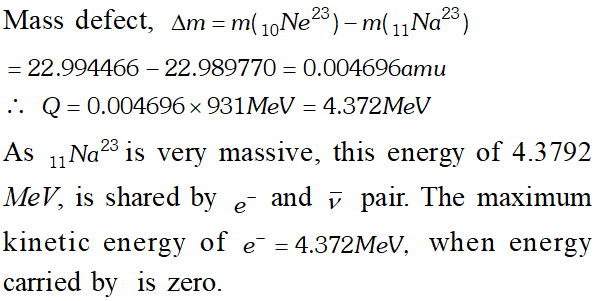
Q. A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much did it contain initially ? Assume that all the energy generated arises from the fission of and that this nuclide is consumed by the fission process. [NCERT]
Ans. In the fission of one nucleus of $_{92} U^{285}$ energy generated is 200 $M e V .$ 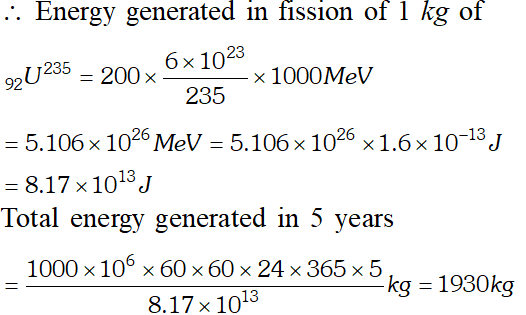
Q. How long can an electric lamp of 100 W be kept glowing by fusing of 2.0 kg of deuterium ? The fusion reaction can be taken as [NCERT]
Ans. Number of deuterium atoms in 2.0 kg $=\frac{6.023 \times 10^{23} \times 2000}{2}=6.023 \times 10^{26}$
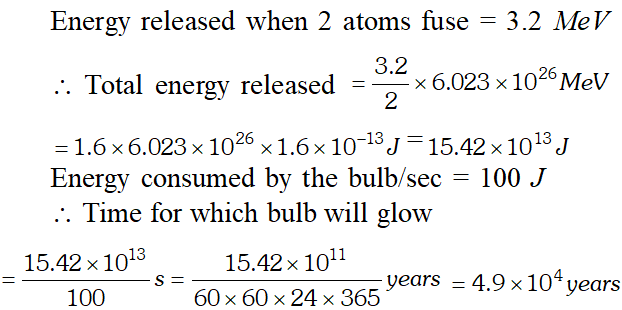
Q. Calculate binding energy per nucleon of $40 \mathrm{Ca}$ nucleus (given mass of $\frac{40}{20} \mathrm{Ca}=39.962589 \mathrm{u}$ mass of proton $=1.0078254,$ mass of neutron $=1.0086654$ 1 atomic mass unit $(1 \mathrm{u})=931 \mathrm{MeV})$
Ans. Nucleus $\frac{40}{20} \mathrm{Ca}$ has 20 protons and 20 neutrons Mass of 20 protons $=1.007825 \times 20=20.1565$ amu Mass of 20 neutrons $=1.008665 \times 20=20.1733$ amu Total mass $=40.2298 \mathrm{amu}$ Mass of nucleus $=39.962589$ amu $\therefore$ Mass defect $\Delta m=40.2298-39.962589=0.267211$ amu So B.E. per nucleon $=\frac{\Delta m \times 931}{A}=\frac{0.267211 \times 931}{40}$ $=6.22 \mathrm{MeV} /$ nucleon.


![]()
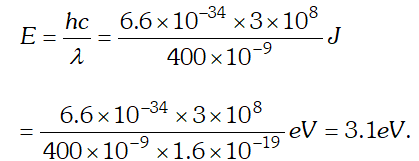
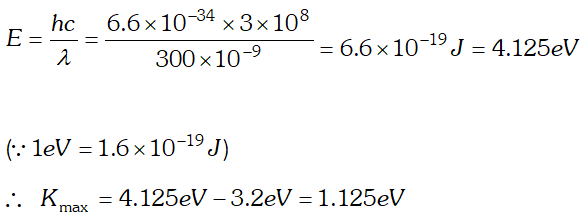

![]() $=3.84 \times 10^{21}$ photons/m'-s
$=3.84 \times 10^{21}$ photons/m'-s 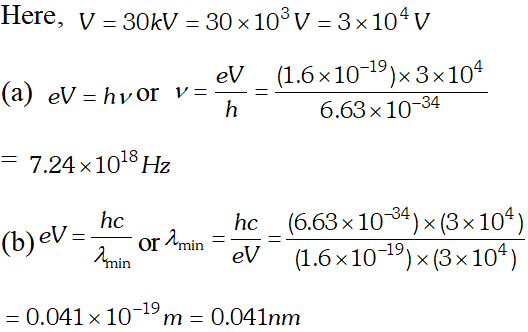
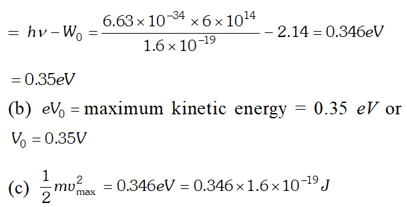
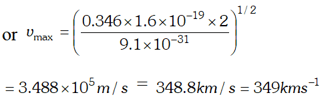
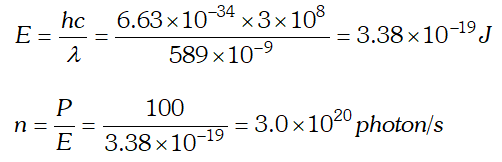
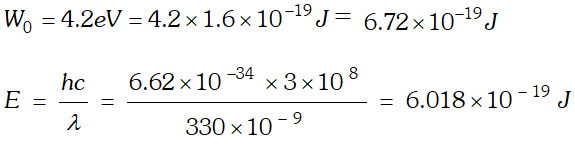 As energy of incident photon $E
As energy of incident photon $E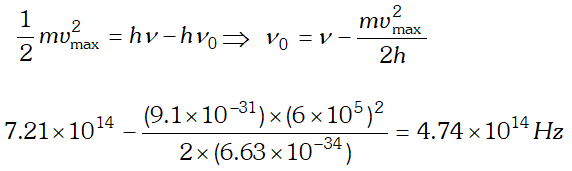
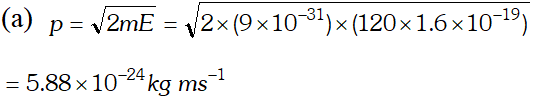
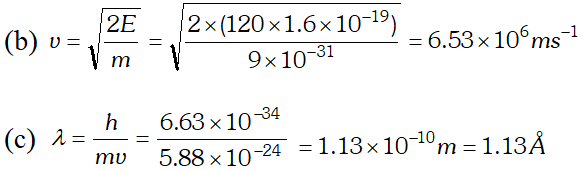
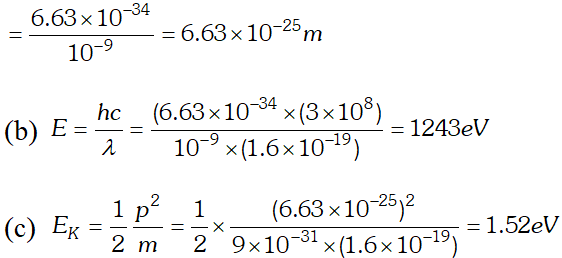
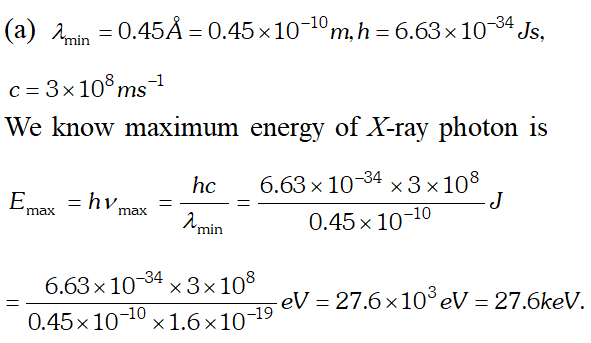 (b) In X-ray tube, accelerating voltage provides the energy to the electrons which on striking the anti-cathode, produce X-ray for getting X-ray photons of 27.6 keV, it is required that the incident electrons must possess kinetic energy of at least 27.6 keV. Therefore accelerating voltage of the order of 30 keV should be applied across the X-ray tube to get the required X-ray photons.
(b) In X-ray tube, accelerating voltage provides the energy to the electrons which on striking the anti-cathode, produce X-ray for getting X-ray photons of 27.6 keV, it is required that the incident electrons must possess kinetic energy of at least 27.6 keV. Therefore accelerating voltage of the order of 30 keV should be applied across the X-ray tube to get the required X-ray photons. 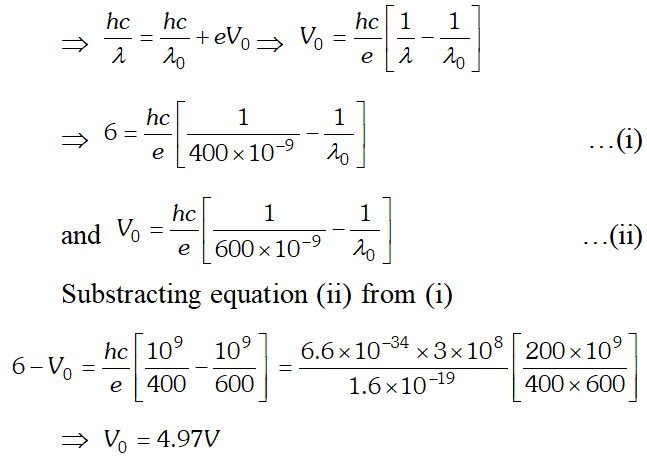
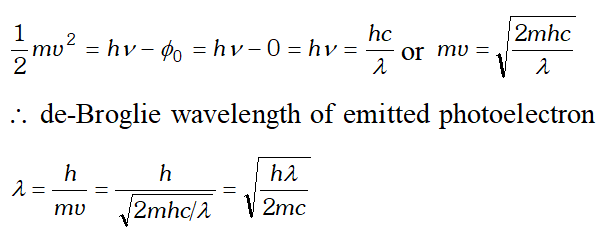
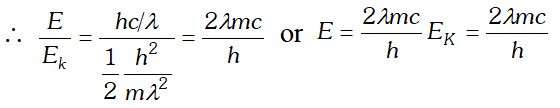

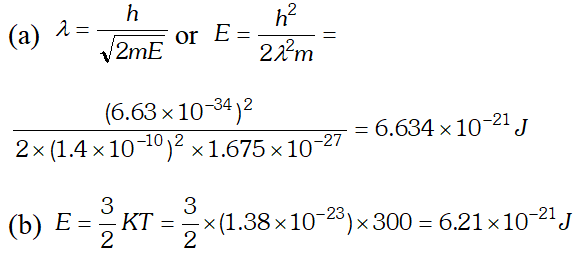
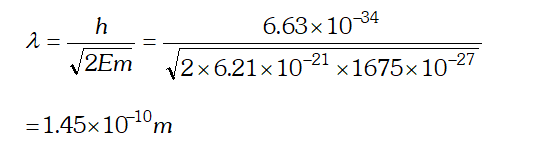
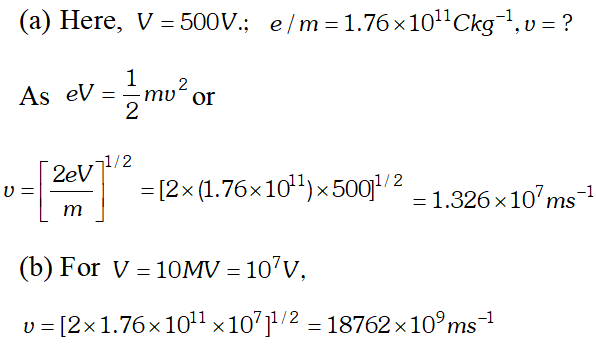 As this speed is greater than the speed of light, so this speed is not possible because as v approaches c, mass of electron becomes infinite $\left[\because m=\frac{m_{0}}{\sqrt{1-v^{2} / C^{2}}}\right]$ so the formula has to be modified.
As this speed is greater than the speed of light, so this speed is not possible because as v approaches c, mass of electron becomes infinite $\left[\because m=\frac{m_{0}}{\sqrt{1-v^{2} / C^{2}}}\right]$ so the formula has to be modified. 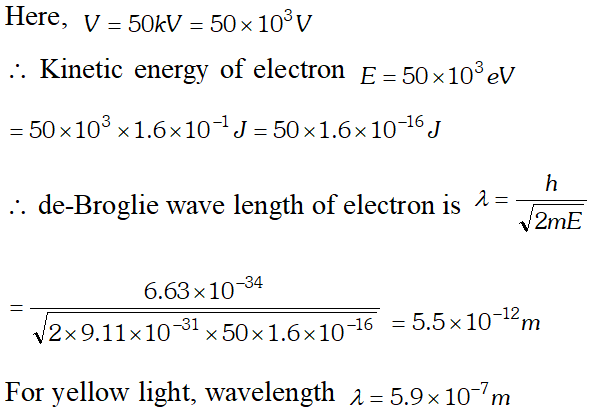
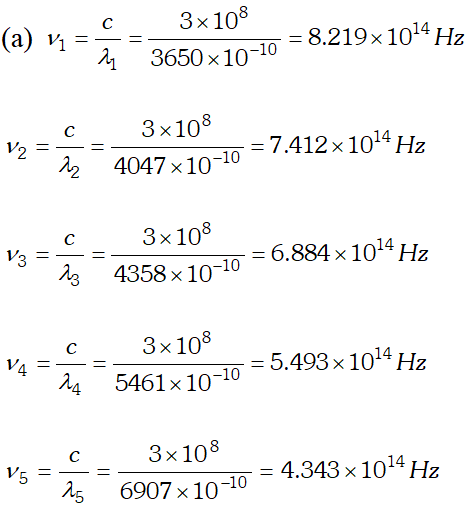 We know that, $e V_{0}=h v-W_{0}$ $\Rightarrow V_{0}=\frac{h v}{e}-\frac{W_{0}}{e}$ Hence a graph between frequency and stopping potential $V_{0}$, must be a straight line. On plotting a graph between given frequencies and corresponding values of stopping potentials we get a straight line with first four points. This straight line is cutting v-axis at $5.0 \times 10^{14} \mathrm{Hz}$ The fifth point comes in the range of $v
We know that, $e V_{0}=h v-W_{0}$ $\Rightarrow V_{0}=\frac{h v}{e}-\frac{W_{0}}{e}$ Hence a graph between frequency and stopping potential $V_{0}$, must be a straight line. On plotting a graph between given frequencies and corresponding values of stopping potentials we get a straight line with first four points. This straight line is cutting v-axis at $5.0 \times 10^{14} \mathrm{Hz}$ The fifth point comes in the range of $v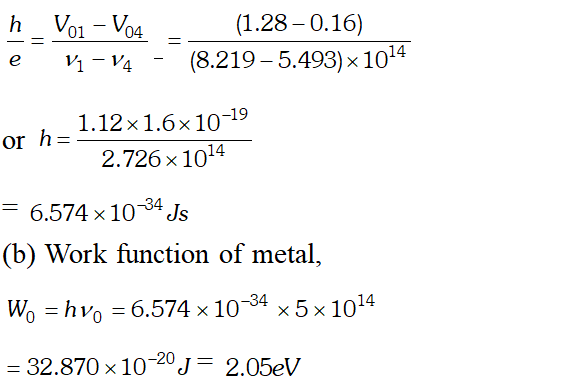
 By applying suitable voltage from a high voltage power supply (H.T. or battery), they are made to pass through a cylinder with fine holes along its axis, producing a fine collimated beam. The beam is made to fall on the surface of a nickel crystal. The electrons are scattered in all directions by the atoms of the crystal. The intensity of the electron beam, scattered in a given direction, is measured by the electron detector (collector). The detector can be moved on a circular scale and is connected to a sensitive galvanometer, which records the current. The deflection of the galvanometer is proportional to the intensity of the electron beam entering the collector. The apparatus is enclosed in an evacuated chamber. By moving the detector on the circular scale at different positions, the intensity of the scattered electron beam is measured for different values of an angle of scattering $\theta$ which is the angle between the incident and the scattered electron beams. The variation of intensity (I) of the scattered electrons with the angle of scattering $\theta$ is obtained for different accelerating voltages. The experiment was performed by varying the accelerating voltage from 44 V to 68 V. It was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle $\theta=50^{\circ}$ From the electron diffraction measurements the wavelength of matter waves was found to be 0.165 nm. The de-Broglie wavelength $\lambda$ associated with electrons using equation for is given by $\lambda=h / p=\frac{12.27}{\sqrt{V}}=n m \Rightarrow \lambda=\frac{1.22}{\sqrt{54}} n m=0.167 n m$ Davisson Germer experiment thus strikingly confirms the wave nature of electrons and the de-Broglie relation
By applying suitable voltage from a high voltage power supply (H.T. or battery), they are made to pass through a cylinder with fine holes along its axis, producing a fine collimated beam. The beam is made to fall on the surface of a nickel crystal. The electrons are scattered in all directions by the atoms of the crystal. The intensity of the electron beam, scattered in a given direction, is measured by the electron detector (collector). The detector can be moved on a circular scale and is connected to a sensitive galvanometer, which records the current. The deflection of the galvanometer is proportional to the intensity of the electron beam entering the collector. The apparatus is enclosed in an evacuated chamber. By moving the detector on the circular scale at different positions, the intensity of the scattered electron beam is measured for different values of an angle of scattering $\theta$ which is the angle between the incident and the scattered electron beams. The variation of intensity (I) of the scattered electrons with the angle of scattering $\theta$ is obtained for different accelerating voltages. The experiment was performed by varying the accelerating voltage from 44 V to 68 V. It was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle $\theta=50^{\circ}$ From the electron diffraction measurements the wavelength of matter waves was found to be 0.165 nm. The de-Broglie wavelength $\lambda$ associated with electrons using equation for is given by $\lambda=h / p=\frac{12.27}{\sqrt{V}}=n m \Rightarrow \lambda=\frac{1.22}{\sqrt{54}} n m=0.167 n m$ Davisson Germer experiment thus strikingly confirms the wave nature of electrons and the de-Broglie relation  The minimum number of photons can be one only corresponding to the transition $4 \rightarrow 1$
The minimum number of photons can be one only corresponding to the transition $4 \rightarrow 1$ 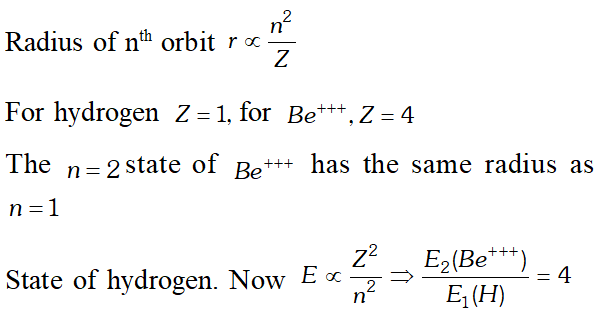
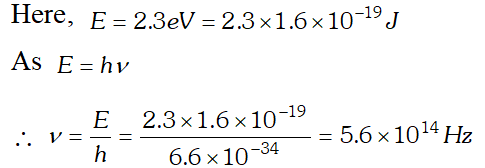
![]()
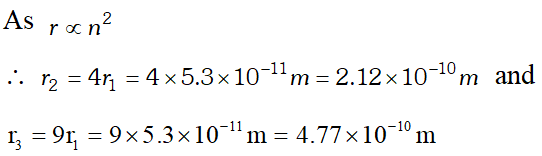
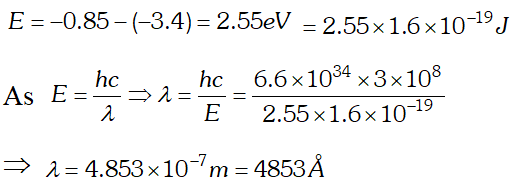 This wavelength belongs to Balmer series of hydrogen spectrum.
This wavelength belongs to Balmer series of hydrogen spectrum. 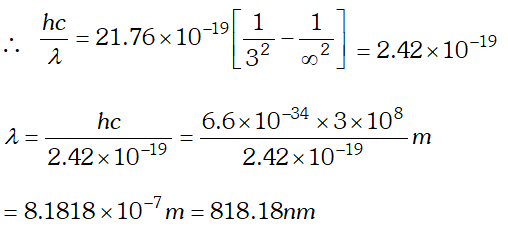
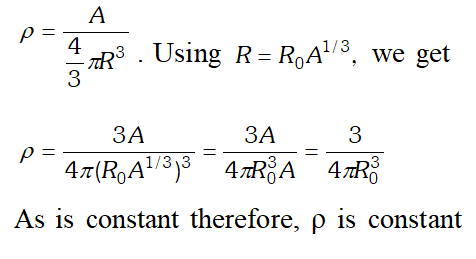
 From the curve it is clear that binding energy per nucleon is maximum for iron $\left(_{26} F e^{56}\right)$ having mass number 56, so it is most stable. The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.
From the curve it is clear that binding energy per nucleon is maximum for iron $\left(_{26} F e^{56}\right)$ having mass number 56, so it is most stable. The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei. ![]() Taking loge both the sides we get
Taking loge both the sides we get ![]() This is the required relation
This is the required relation  The potential energy is minimum at a distance $r_{0} \approx 0.8 \mathrm{fm}$ This means that the force is attractive for distances larger than 0.8 fm and repulsive if nucleons separated by distance less than 0.8 fm.
The potential energy is minimum at a distance $r_{0} \approx 0.8 \mathrm{fm}$ This means that the force is attractive for distances larger than 0.8 fm and repulsive if nucleons separated by distance less than 0.8 fm.