Hey, do you want to learn about the Motion in a lift? If yes. Then keep reading.
We consider the following cases:
Case (a)
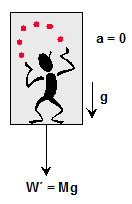
If the lift moving with constant velocity v upwards or downwards.
In this case, there is no accelerated motion hence no pseudo force experienced by observer $0^{\prime}$ inside the lift.
So apparent weight $\mathrm{W}^{\prime}$ = Actual weight W.
Case (b)
If the lift is accelerated (i.e. a = constant upward) : Then net forces acting on the man are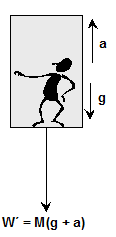
So apparent weight
$W^{\prime}=W+F_{0}$
Or
$\mathrm{W}^{\prime}=\mathrm{Mg}+\mathrm{Ma}$
$=M(g+a)$
Effective gravitational acceleration
$g^{\prime}=g+a$
Case (c)
If the lift is accelerated downward with acceleration $a: Then fictitious force $\mathrm{F}_{0}$ = Ma acts upward while the weight of man W = Mg always acts downward, therefore
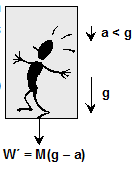
So apparent weight
$W^{\prime}=W+F_{0}$
Or
$\mathrm{W}^{\prime}=\mathrm{Mg}-\mathrm{Ma}$
$=M(g-a)$
Effective gravitational acceleration
$g^{\prime}=g-a$
Special Case:
If g = a then
$W^{\prime}=0$ cond $^{n}$. Of weightlessness.
Thus, in a freely falling lift the man will experience weightlessness.
Case (d)
If lift accelerates downward with acceleration a > g
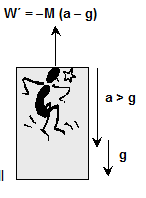
Then as in Case c
Apparent weight $W^{\prime}=M(g-a)$ = $-M(a-g)$ is negative, i.e., the man will be accelerated upward and will stay at the ceiling of the lift.
Ex. A spring weighing machine inside a stationary lift reads 50 kg when a man stands on it. What would happen to the scale reading if the lift is moving upward with (i) constant velocity, and (ii) constant acceleration?
Sol. (i) In the case of a constant velocity of lift, there is no fictitious force; therefore, the apparent weight = actual weight. Hence the reading of the machine is 50 kg wt.
(ii) In this case the acceleration is upward, the fictitious force R = ma acts downward, therefore apparent weight is more than actual weight i.e. $\mathrm{W}^{\prime}$ = W + R = m (g + a).
Hence scale shows a reading = m (g + a) newton
$=\frac{m g\left(1+\frac{a}{g}\right)}{g} k g$
$=\left(50+\frac{50 a}{g}\right) k g.w t$
So, that's all from this blog. I hope you get the idea about the Motion in a lift. If you found this article helpful then don't forget to share it with your friends.
Also, read
Frame of reference
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Motion in a Lift
The weight of a body is simply the force exerted by the earth on the body. If the body is on an accelerated platform, the body experiences a fictitious force, so the weight of the body appears changed and this new weight is called apparent weight. Let a man of weight W = Mg be standing in a lift.We consider the following cases:
Case (a)
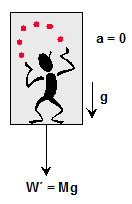
If the lift moving with constant velocity v upwards or downwards.
In this case, there is no accelerated motion hence no pseudo force experienced by observer $0^{\prime}$ inside the lift.
So apparent weight $\mathrm{W}^{\prime}$ = Actual weight W.
Case (b)
If the lift is accelerated (i.e. a = constant upward) : Then net forces acting on the man are
- weight W = Mg downward
- fictitious force $\mathrm{F}_{0}$ = Ma downward.
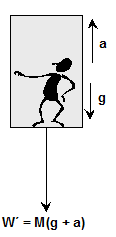
So apparent weight
$W^{\prime}=W+F_{0}$
Or
$\mathrm{W}^{\prime}=\mathrm{Mg}+\mathrm{Ma}$
$=M(g+a)$
Effective gravitational acceleration
$g^{\prime}=g+a$
Case (c)
If the lift is accelerated downward with acceleration $a
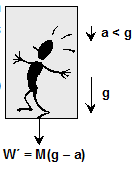
So apparent weight
$W^{\prime}=W+F_{0}$
Or
$\mathrm{W}^{\prime}=\mathrm{Mg}-\mathrm{Ma}$
$=M(g-a)$
Effective gravitational acceleration
$g^{\prime}=g-a$
Special Case:
If g = a then
$W^{\prime}=0$ cond $^{n}$. Of weightlessness.
Thus, in a freely falling lift the man will experience weightlessness.
Case (d)
If lift accelerates downward with acceleration a > g

Then as in Case c
Apparent weight $W^{\prime}=M(g-a)$ = $-M(a-g)$ is negative, i.e., the man will be accelerated upward and will stay at the ceiling of the lift.
Ex. A spring weighing machine inside a stationary lift reads 50 kg when a man stands on it. What would happen to the scale reading if the lift is moving upward with (i) constant velocity, and (ii) constant acceleration?
Sol. (i) In the case of a constant velocity of lift, there is no fictitious force; therefore, the apparent weight = actual weight. Hence the reading of the machine is 50 kg wt.
(ii) In this case the acceleration is upward, the fictitious force R = ma acts downward, therefore apparent weight is more than actual weight i.e. $\mathrm{W}^{\prime}$ = W + R = m (g + a).
Hence scale shows a reading = m (g + a) newton
$=\frac{m g\left(1+\frac{a}{g}\right)}{g} k g$
$=\left(50+\frac{50 a}{g}\right) k g.w t$
So, that's all from this blog. I hope you get the idea about the Motion in a lift. If you found this article helpful then don't forget to share it with your friends.
Also, read
Frame of reference
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Comments
Madhu
Sept. 27, 2024, 6:35 a.m.
Thanks this helped a lot the diagrams are self explanatory 😁.
This blog really helped me to dispel all my confusion
Lubita Lorraine Kagusa
July 25, 2024, 6:01 p.m.
i enjoyed reading and have understood i just hope for more detail
Tuli nath
Feb. 13, 2023, 5:25 p.m.
What if the velocity is given and we need to find the force at which the lift falls down
