Get Motion in a Straight Line Class 11 problems with Solutions for Boards exams. View the Physics Question Bank for class 11 and 12 and find other chapters' problems with solution too along with Motion in a Straight Line chapter. These important questions will play significant role in clearing concepts of Physics. This question bank is designed by keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 12 Physics chapter wise CBSE. Keep reading for Motion in a Straight Line Class 11 Problems with Solutions: Click Here for Detailed Chapter-wise Notes of PHYSICS for Class 12th, JEE & NEET.
Motion in a Straight Line Class 11 Problems with Solutions
Q. Can a body be said to be at rest as well as in motion at the same time.
Ans. Yes, rest and motion are relative terms. A body at rest with respect to one body may be in motion with respect to another body.
Q. Can a body have zero velocity but yet possesses acceleration?
Ans. Yes, When a body is projected upward, at the highest point its velocity is zero but the acceleration is g.
Q. Under what condition will the distance and displacement of a moving object will have the same magnitude?
Ans. It indicates Instantaneous speed.
Q. What does speedometer of a car indicate?
Ans. It indicates Instantaneous speed.
Q. As the body moves in a straight line, it moves smaller and smaller distances in equal intervals of time.
Ans.Β The Body is Retarded
Q. Derive an expression for stopping distance of a vehicle in terms of initial velocity and deceleration a. [NCERT]
Ans. Let $\mathrm{d}_{\mathrm{s}}$ be the distance travelled by a vehicle before it stops. Using $\mathrm{v}^{2}-\mathrm{u}^{2}=2 \mathrm{aS},$ we get, $0^{2}-\mathrm{v}_{0}^{2}=-2 \mathrm{ad}_{\mathrm{s}}$ $\mathrm{d}_{\mathrm{s}}=\frac{\mathrm{v}_{0}^{2}}{2 \mathrm{a}}$ The stopping distance is proportional to the square of the initial velocity. Doubling the initial velocity increase the stopping distance by a factor $4,$ provided deceleration is kept the same.
Q. Explain clearly, with examples, the distinction between : (a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval; (b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the quality sign true? [NCERT]
Ans. (a) Consider a particle which moves form $A$ to $B$ and then back to $A$. In this case, the magnitude of displacement is zero. This is because the magnitude of displacement is equal to the shorteddistance between initial and final positions of the particle. If $B$ is separated from $A$ by a distance $x$, then the total path length travelled by the particle is $2 x$. (b) Average velocity $=\frac{\text { Displacement }}{\text { Time }}=\frac{0}{t}=0$ Average speed $=\frac{\text { Total path length }}{\text { Corresponding time interval }}=\frac{2 x}{t}$
Q. Derive three equations of motion by calculus method. Express conditions under which they can be used.
Ans. (1) $\mathrm{v}=\mathrm{u}+\mathrm{at}$ : Let any instant $t$, the velocity of a particle is $v$ $\therefore$ Acceleration, $a=\frac{d v}{d t} \Rightarrow d v=a d t$ Let at $t=0, v=u$ $\therefore$ Integrating equation (i), we get $\int_{u}^{v} d v=\int_{0}^{t} a d t \Rightarrow \int_{u}^{v} d v=a \int_{0}^{t} d t \quad \therefore[v]_{u}^{v}=a[t]_{0}^{t}$ $\therefore(\mathrm{v}-\mathrm{u})=\mathrm{a}(\mathrm{t}-0) \Rightarrow \mathrm{v}-\mathrm{u}=\mathrm{at} \Rightarrow \mathrm{v}=\mathrm{u}+\mathrm{at}$ (2) $\mathrm{s}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}:$ Let a particle is moving with velocity $u,$ along $X$ -axis and at any instant $t,$ its displacement is $x$ $\therefore \mathrm{v}=\frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}} \Rightarrow \mathrm{dx}=\mathrm{v} \mathrm{dt}$ Also, we know that, $\mathrm{v}=\mathrm{u}+\mathrm{at}$ $\therefore \mathrm{dx}=(\mathrm{u}+\mathrm{at}) \mathrm{dt}$ -----(i) Now, at $\mathrm{t}=0, \mathrm{x}=\mathrm{x}_{0}$ $\therefore$ Integrating equation (i), we get $\int_{x_{0}}^{x} d x=\int_{0}^{t}(u+a t) d t \Rightarrow[x]_{x_{0}}^{x}=\int_{0}^{t} u d t+\int_{0}^{t} a t d t$ $\Rightarrow \quad \mathrm{x}-\mathrm{x}_{0}=\mathrm{u}[\mathrm{t}]_{0}^{\mathrm{t}}+\mathrm{a}\left[\frac{\mathrm{t}^{2}}{2}\right]_{0}^{\mathrm{t}}$ $\Rightarrow \quad \mathrm{x}-\mathrm{x}_{0}=\mathrm{u}(\mathrm{t}-0)+\mathrm{a}\left(\frac{\mathrm{t}^{2}}{2}-0\right)$ $\Rightarrow \mathrm{x}-\mathrm{x}_{0}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}$ But, $\mathrm{x}-\mathrm{x}_{0}=\mathrm{s} \quad \therefore \mathrm{s}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}$ (3) $\mathrm{v}^{2}=\mathrm{u}^{2}+2 \mathrm{as} \quad:$ Now we know that, $\mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\mathrm{dv}}{\mathrm{dx}} \times \frac{\mathrm{dx}}{\mathrm{dt}}$ $\therefore \mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dx}} \cdot \mathrm{v} \Rightarrow \mathrm{a} \mathrm{dx}=\mathrm{v} \mathrm{dv}\left[\because \mathrm{v}=\frac{\mathrm{dx}}{\mathrm{dt}}\right]$ Now limits, when $\mathrm{t}=0, \mathrm{x}=\mathrm{x}_{0}$ and $\mathrm{v}=\mathrm{u} \ldots \ldots$ --(i) And when $\mathrm{t}=\mathrm{t}, \mathrm{x}=\mathrm{x}$ and $\mathrm{v}=\mathrm{v}$ Integrating the equation (i), we get $\int_{x_{0}}^{x} a d x=\int_{u}^{v} v d v \Rightarrow a[x]_{x_{0}}^{x}=\left[\frac{v^{2}}{2}\right]_{u}^{v}$ $\Rightarrow \mathrm{a}\left(\mathrm{x}-\mathrm{x}_{0}\right)=\left[\frac{\mathrm{v}^{2}}{2}-\frac{\mathrm{u}^{2}}{2}\right]$ But, $\mathrm{x}-\mathrm{x}_{0}=\mathrm{s}$ $\therefore \quad \mathrm{as}=\frac{\mathrm{v}^{2}-\mathrm{u}^{2}}{2} \Rightarrow \mathrm{v}^{2}-\mathrm{u}^{2}=2 \mathrm{as}$ $\therefore \mathrm{v}^{2}=\mathrm{u}^{2}+2 \mathrm{as}$
Q. Can a body have constant velocity and still have varying speed?
Ans. Not possible.
Q. Are rest and motion absolute or relative terms?
Ans. Both rest and motion are Relative Terms
Q. Why the speed of the object can never be negative?
Ans. Speed is distance covered per unit time. since distance cannot be negative there fore speed cannot be negative.
Q. Define instantaneous velocity. Sol. Velocity of a body at a particular instant is called Instantaneous velocity. $\mathrm{v}=\frac{\mathrm{dx}}{\mathrm{dt}}$ and $\operatorname{Lt}_{\mathrm{st} \rightarrow 0}\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)$
Q. What is average velocity?
Ans. Avg. Velocity: The Ratio of Total Displacement and total time Taken is said as average Velocity. i.e. Average velocity $=\frac{\text { Total displacement }}{\text { Total time }}$ If the position of a particle in time $t$ and t'are $x(t)$ and $x\left(t^{\prime}\right),$ then, $V_{a v}=\frac{x\left(t^{\prime}\right)-x(t)}{t^{\prime}-t}=\frac{\Delta x}{\Delta t}$
Q. The position of an object moving along -axis is given by where and is measured in second. What is it velocity at and . What is the average velocity between and [NCERT]
Ans. $\mathrm{v}=\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{a}+\mathrm{bt}^{2}\right)=2 \mathrm{bt}=5.0 \mathrm{tms}^{-1}$ At $\mathrm{t}=-\mathrm{s}, \mathrm{v}=0 \mathrm{ms}^{-1}$ and at $\mathrm{t}=2 \mathrm{s}, \mathrm{v}=10 \mathrm{ms}^{-1}$ Average Velocity =$\frac{x(4)-x(2)}{4-2}=\frac{a+16 b-a-4 b}{2}=6 b$ $=6 \times 2.5=15.0 \mathrm{ms}^{-1}$
Q. A jet air plane travelling at the speed of ejects its products of combustion at the speed to relative to the jet plane. What is the speed of the combustion products w.r.t. an observer on the ground? [NCERT]
Ans. Speed of combustion product w.r.t. observer on the ground $=?$ Velocity of jet air plane w.r.t. observer on ground $=500 \mathrm{kmh}^{-1}$ If $\overrightarrow{\mathrm{v}}_{\mathrm{j}}$ and $\overrightarrow{\mathrm{v}}_{\mathrm{o}}$ represent the velocities of jet and observer respectively, then $\mathrm{v}_{\mathrm{j}}-\mathrm{v}_{\mathrm{o}}=500 \mathrm{kmh}^{-1}$ Similarly, If $\vec{v}_{\mathrm{c}}$ represents the velocity of the combustion products $w \cdot r .$ jet plane, then, $\mathrm{v}_{\mathrm{c}}-\mathrm{v}_{\mathrm{j}}=-1500 \mathrm{kmh}^{-1}$ The negative sign indicates that the combustion products move in a direction opposite to that of jet. Speed of combustion products w.r.t. observer $=v_{c}-v_{o}=\left(v_{c}-v_{j}\right)+\left(v_{j}-v_{o}\right)$ $=(-1500+500) \mathrm{kmh}^{-1}=-1000 \mathrm{kmh}^{-1}$
Q. A police van moving on a highway with a speed of fires a bullet at a thief's car speeding away in the same direction with a speed of . If the muzzle speed of the bullet is , with what speed does the bullet hit the thief's car? [NCERT]
Ans. Speed of bullet, $v_{b}=$ speed of police vant speed with which bullet is actually fired $\therefore \quad v_{b}=\left(\frac{25}{3}+150\right) \mathrm{ms}^{-1}=\frac{475}{3} \mathrm{ms}^{-1}$ Relative velocity of bullet w.r.t. thief's car, $\mathrm{v}_{\mathrm{bt}}=\mathrm{v}_{\mathrm{b}}-\mathrm{v}_{\mathrm{t}}=\left(\frac{475}{3}-\frac{160}{3}\right) \mathrm{ms}^{-1}=105 \mathrm{ms}^{-1}$''
Q. Four persons K, L, M and start from the vertices of a square of side , simultaneously and move towards the neighbour in order always with the same speed of . When and where do they meet. [NCERT]
Ans.As $K, L, M$ and $N$ move towards the next person in order after a short time they will be at $K^{\prime}, L^{\prime}$ $M^{\prime}$ and $N^{\prime}$ respectively. The size to the square reduces. It indicates that they have come closer. After next short interval if they are at $K^{\prime \prime}, L^{\prime \prime}$ $M^{\prime \prime}$ and $N^{\prime \prime},$ the size of the square further reduces. Finally, they will follow a curvi-linear path and meet at $O,$ the centre of the square. We know, the time taken $=\frac{\text { displacement }}{\text { Velocity in the direction of displacement }}$ 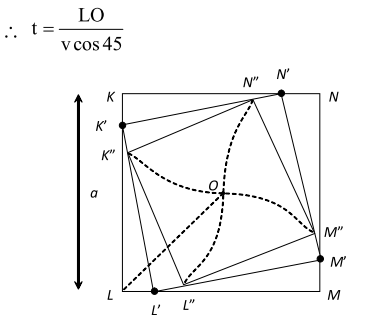Β
$\therefore \quad \mathrm{t}=\frac{\mathrm{LO}}{\left(\frac{\mathrm{v}}{\sqrt{2}}\right)}=\frac{\frac{\mathrm{a}}{\sqrt{2}}}{\frac{\mathrm{v}}{\sqrt{2}}}=\frac{\mathrm{a}}{\mathrm{v}}$ Q. On a two-lane road, car is travelling with a speed of . Two cars and approach car in opposite directions with a speed of each. At a certain instant, when distance. A B is equal to A C, both being decides to overtake before does. What minimum acceleration of is required to avoid an accident? [NCERT]
Ans. $v_{A}=36 \mathrm{kmh}^{-1}=36 \times \frac{5}{18} \mathrm{ms}^{-1}=10 \mathrm{ms}^{-1}$ $v_{B}=v_{\mathrm{c}}=54 \mathrm{kmh}^{-1}=54 \times \frac{5}{18} \mathrm{ms}^{-1}=15 \mathrm{ms}^{-1}$ Relative velocity of $B$ w.t. $A, \quad v_{\mathrm{B}_{\mathrm{A}}}=5 \mathrm{ms}^{-1}$ Relative velocity of $C$ wr.t. $A, \mathrm{v}_{\mathrm{cA}}=25 \mathrm{ms}^{-1}$ Time taken by $C$ to cover distance $\mathrm{AC}=\frac{1000 \mathrm{m}}{25 \mathrm{ms}^{-1}}=40 \mathrm{s}$ Now, for $B$ $1000=5 \times 40+\frac{1}{2} \mathrm{a} \times 40 \times 40$ On simplification
Q. On a long horizontal moving belt, a child runs to and fro with a speed (with respect to the belt between his father and mother located apart on the moving belt. The belt moves with . speed of For an observer on a stationary . platform outside, what is the : (a) speed of the belt child running in the direction of motion of the belt ? (b) speed of the child running opposite to the direction of motion of the belt? (c) time taken by child in (a) and (b)? Which of the answer alter if motion is viewed by one of the parents? [NCERT]
Ans. Speed of child with respect to belt =9 $\mathrm{kmh}^{-1}$;
Speed of belt = 4 $\mathrm{kmh}^{-1}$ (a) When the child runs in the direction of motion Of the belt, then speed of child w.r.t. stationary observer $=(9+4) \mathrm{kmh}^{-1}=13 \mathrm{kmh}^{-1}$ (b) When the child runs opposite to the direction of motion of the belt, then speed of child writ. stationary observer $=(9-4) \mathrm{kmh}^{-1}=5 \mathrm{kmh}^{-1}$ (c) Speed of child w.rt. either parent $=9 \mathrm{kmh}^{-1}$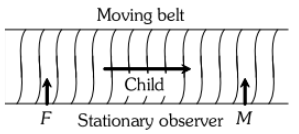 
Distance to be covered $=50 \mathrm{m}=0.05 \mathrm{km} ;$ Time $=\frac{0.05 \mathrm{km}}{9 \mathrm{kmh}^{-1}}=0.0056 \mathrm{h} \approx 20 \mathrm{s}$ If the motion is viewed by one of the parents, then the answers to (a) and (b) are altered but answer to (c) remains unaltered. Q. A man walks on a straight road from his home to a market away with a speed of Finding the market closed, he instantly turns and walks back home with a speed of . What is the (a) magnitude of average velocity, and (b) average speed of the man over the following intervals of time : (i) 0 to 30 min (ii) 0 to 50 min (iii) 0 to 40 min? [NCERT]
Q. A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to . (a) How much time does the ball take to return to his hands b) If the lift starts moving up with a uniform speed of , and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Ans. (a) $\mathrm{v}(0)=49 \mathrm{ms}^{-1}, \mathrm{a}=-9.8 \mathrm{ms}^{-2}, \mathrm{v}(\mathrm{t})=0, \mathrm{t}=?$ $\mathrm{v}(\mathrm{t})=\mathrm{v}(0)+\mathrm{at}$ $\Rightarrow \quad 0=49-9.8 \mathrm{t} \Rightarrow 9.8 \mathrm{t}=49 \Rightarrow \mathrm{t}=\frac{49}{9.8} \mathrm{s}=5 \mathrm{s}$ This is the time taken by the ball to reach the maximum height. The time of descent is also 5 s. So, the total time after which the ball comes back is $5 s+5 s$ i.e., $10 s$ (b) The uniform velocity of the lift does not change the relative motion of ball and lift. So, the ball would take the same total time $i . e .,$ it would come back after 10 second.
Q. A woman starts from her home at $9.00 A M,$ walks with a speed pf on a straight road up to her office away, stays at the office up to and returns home by an auto with a speed of . Choose suitable scales and plot the graph of the motion. [NCERT]
Ans.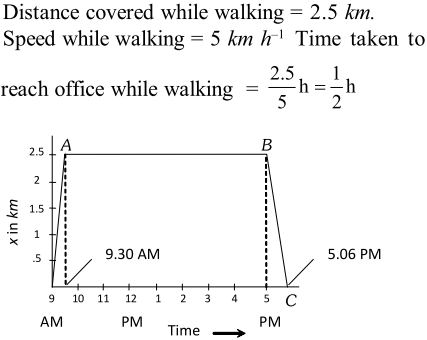 
If $O$ is regarded as the origin for both time and distance, then At $\mathrm{t}=9.00 \mathrm{AM}, \mathrm{x}=0$ and, at $\mathrm{t}=9.30 \mathrm{AM}, \mathrm{x}=2.5 \mathrm{km}$ OA is the $\mathrm{x}-\mathrm{t}$ graph of the motion when the woman walks from her home to office. Her stay in the office from $9.30 \mathrm{AM}$ to $5.00 \mathrm{PM}$ is represented by the straight line $A B$ in the graph. Now, time taken to return home by an auto = $\frac{2.5}{25} \mathrm{h}=\frac{1}{10} \mathrm{h}=6$ minuteSo, at $\mathrm{t}=5.06 \mathrm{PM}, \mathrm{x}=0$
