Hey, do you want to learn about the motion of bodies connected by strings? If yes. Then you are at the right place.
Let us consider the case of two bodies of masses $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ connected by a thread and placed on a smooth horizontal surface as shown in fig. A force F is applied on the body of mass $\mathrm{m}_{2}$ in forwarding direction as shown. Our aim is to consider the acceleration of the system and the tension T in the thread. The forces acting separately on two bodies are also shown in the figure:
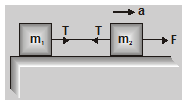
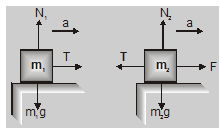
From fig
$\mathrm{T}=\mathrm{m}_{1} \mathrm{a}$.....(1)
$F-T=m_{2} a$.....(2)
Adding (1) and (2)
$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$
Or
$a=\frac{F}{m_{1}+m_{2}}$.....(3)
The acceleration of the system can be calculated from eq. (3) and tension in the thread by eq. (1).
Three bodies :
In the case of three bodies, the situation is shown in fig.
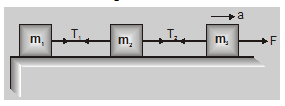
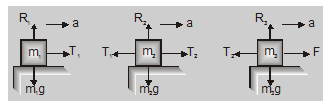
Acceleration $\mathrm{a}=\frac{\mathrm{F}}{\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}}$....(4)
$T_{1}=m_{1} a=\frac{m_{1} F}{m_{1}+m_{2}+m_{3}}$.....(5)
$\mathrm{F}-\mathrm{T}_{2}=\mathrm{m}_{3} \mathrm{a}$
Or
$\mathrm{T}_{2}=\mathrm{F}-\frac{\mathrm{m}_{3} \mathrm{~F}}{\mathrm{~m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}}$
$=\frac{\left(m_{1}+m_{2}\right) F}{m_{1}+m_{2}+m_{3}}$ …..(6)
Ex. Three blocks, are connected by string as shown in fig. below, and are pulled by a force $\mathrm{T}_{3}$ = 120N. If $\mathrm{m}_{1}$ = 5 kg, $\mathrm{m}_{2}$ = 10 kg and $\mathrm{m}_{3}$ = 15 kg. Calculate the acceleration of the system and $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$.
Sol. Acceleration of the system
$a=\frac{F}{m_{1}+m_{2}+m_{3}}$
$=\frac{120}{5+10+15}$
$=4 \mathrm{~m} / \mathrm{sec}^{2}$
Now
$T_{1}=m_{1} a$
$=5 \times 4=20 \mathrm{~N}$
$T_{2}=\left(m_{1}+m_{2}\right) a$
$=(5+10) 4$
$=60 \mathrm{~N}$
So, that's all from this blog, I hope you get the idea about the motion of bodies connected by strings. If you liked this article then please share it with your friends. If you have any confusion related to this article then feel free to ask in the comments section down below.
Also, read
Motion of bodies in contact
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
The motion of bodies connected by strings
Two bodies :Let us consider the case of two bodies of masses $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ connected by a thread and placed on a smooth horizontal surface as shown in fig. A force F is applied on the body of mass $\mathrm{m}_{2}$ in forwarding direction as shown. Our aim is to consider the acceleration of the system and the tension T in the thread. The forces acting separately on two bodies are also shown in the figure:
From fig
$\mathrm{T}=\mathrm{m}_{1} \mathrm{a}$.....(1)
$F-T=m_{2} a$.....(2)
Adding (1) and (2)
$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$
Or
$a=\frac{F}{m_{1}+m_{2}}$.....(3)
The acceleration of the system can be calculated from eq. (3) and tension in the thread by eq. (1).
Three bodies :
In the case of three bodies, the situation is shown in fig.
Acceleration $\mathrm{a}=\frac{\mathrm{F}}{\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}}$....(4)
$T_{1}=m_{1} a=\frac{m_{1} F}{m_{1}+m_{2}+m_{3}}$.....(5)
$\mathrm{F}-\mathrm{T}_{2}=\mathrm{m}_{3} \mathrm{a}$
Or
$\mathrm{T}_{2}=\mathrm{F}-\frac{\mathrm{m}_{3} \mathrm{~F}}{\mathrm{~m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}}$
$=\frac{\left(m_{1}+m_{2}\right) F}{m_{1}+m_{2}+m_{3}}$ …..(6)
Ex. Three blocks, are connected by string as shown in fig. below, and are pulled by a force $\mathrm{T}_{3}$ = 120N. If $\mathrm{m}_{1}$ = 5 kg, $\mathrm{m}_{2}$ = 10 kg and $\mathrm{m}_{3}$ = 15 kg. Calculate the acceleration of the system and $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$.
Sol. Acceleration of the system
$a=\frac{F}{m_{1}+m_{2}+m_{3}}$
$=\frac{120}{5+10+15}$
$=4 \mathrm{~m} / \mathrm{sec}^{2}$
Now
$T_{1}=m_{1} a$
$=5 \times 4=20 \mathrm{~N}$
$T_{2}=\left(m_{1}+m_{2}\right) a$
$=(5+10) 4$
$=60 \mathrm{~N}$
So, that's all from this blog, I hope you get the idea about the motion of bodies connected by strings. If you liked this article then please share it with your friends. If you have any confusion related to this article then feel free to ask in the comments section down below.
Also, read
Motion of bodies in contact
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.