NCERT Solutions for Class 10 Maths chapter 5 - AP (2023)

Hey, are you a class 10 student and looking for ways to download NCERT Solutions for Class 10 Maths chapter 5 - AP (2023), If yes. Then NCERT Solutions for Class 10 Maths chapter 5 - AP (2023) is answer for all your questions..

In this article, we have listed NCERT solutions for class 10 Maths Chapter 5 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

Arithmetic progression (AP) is a sequence of numbers where each term is obtained by adding a fixed constant (known as the common difference) to the preceding term. The first term of an arithmetic progression is denoted by "a" and the common difference is denoted by "d".

The importance of arithmetic progression lies in its numerous applications in various fields, including mathematics, physics, finance, and computer science.

India's Best Exam Preparation for Class 10th - Download Now

 If you want to learn and understand class 10 Maths chapter 5 "Arithmetic Progression" in an easy way then you can use these solutions PDF. 

NCERT Solutions helps students to Practice important concepts of subjects easily. Class 10 Maths solutions provide detailed explanations of all the NCERT exercise questions that students can use to clear their doubts instantly.

If you want to score high in your class 10 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 10 Maths chapter 5 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

India's Best Exam Preparation for Class 10th - Download Now

Table of content

• What is Arithmetic Progression 

• Formula for Arithmetic Progression 

• What are Properties of Arithmetic Progressions 

• How to Apply  of Arithmetic Progressions 

• FAQs

Download The PDF of NCERT Solutions for Class 10 Maths Chapter 5 "Arithmetic Progression"

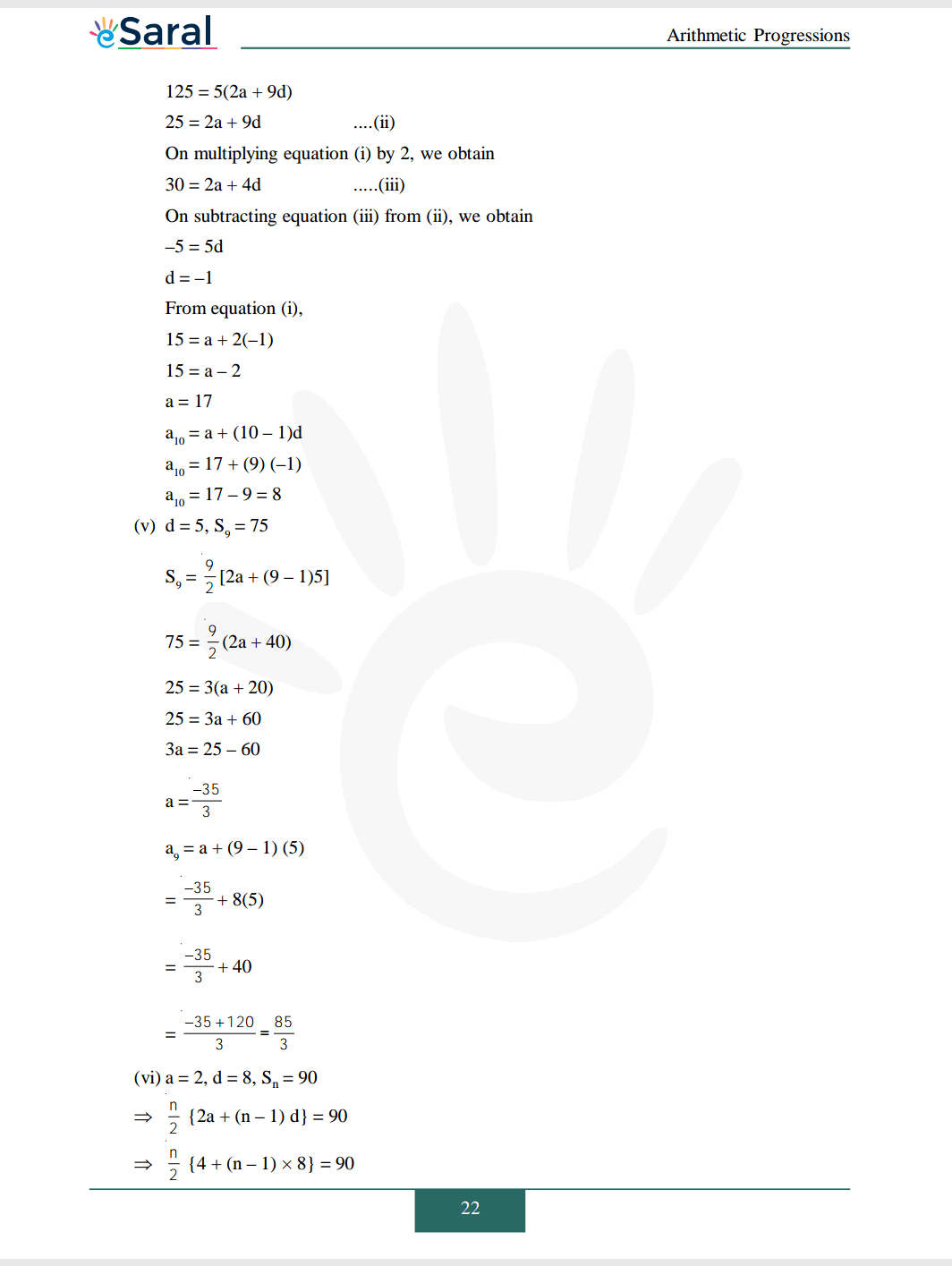
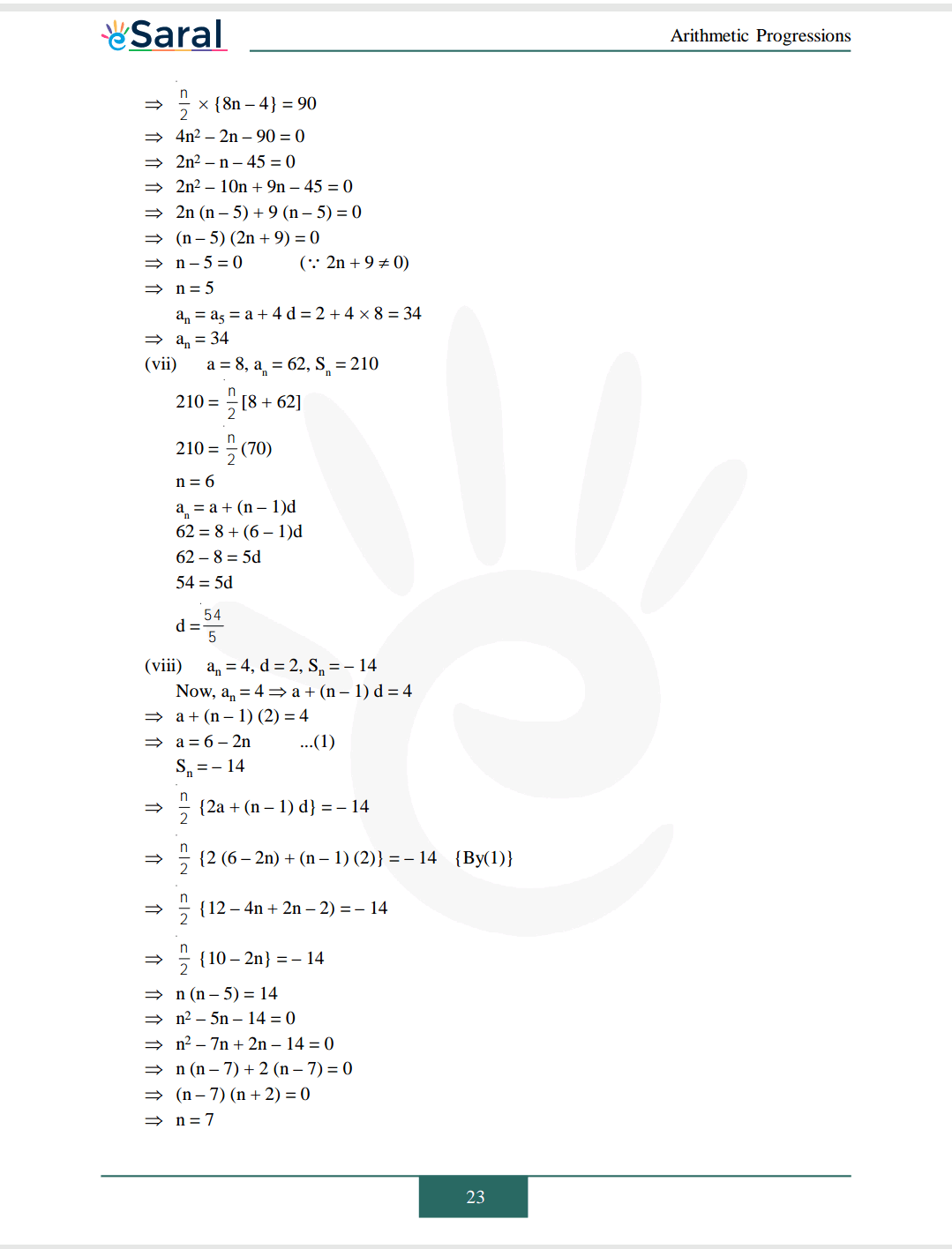
Download The PDF of NCERT Solutions for Class 10 Maths Chapter 5 "Arithmetic Progression"

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

Definition of Arithmetic Progression - NCERT Solutions for Class 10 Maths chapter 5 - AP (2023)

In mathematics, arithmetic progression is an essential topic for studying sequences and series. It helps in understanding the basic principles of mathematical induction, which is used to prove mathematical statements for infinite sets of numbers.

In physics, arithmetic progression is used to model many real-world phenomena, such as uniform motion, time intervals, and periodic events. It provides a framework for understanding the rate of change in these phenomena over time.

In finance, arithmetic progression is used to calculate the depreciation of assets over time. It helps in determining the value of an asset at a particular point in time based on its initial value and the rate of depreciation.

In computer science, arithmetic progression is used in various algorithms for searching and sorting data. It provides a way of organizing data in a systematic manner, which makes it easier to manipulate and analyze.

Formula for Arithmetic Progression - NCERT Solutions for Class 10 Maths chapter 5 - AP (2023)

Here are the formulae for Arithmetic Progressions:

1. nth term formula: $a_n = a_1 + (n-1)d$

2. Sum of n terms formula: $S_n = \frac{n}{2}(2a_1 + (n-1)d)$

Where $a_n$ represents the nth term of the arithmetic progression, $a_1$ is the first term, $d$ is the common difference, and $S_n$ represents the sum of the first n terms of the arithmetic progression.

Properties of Arithmetic Progressions

One important property of arithmetic progressions is that the nth term can be obtained by adding the common difference to the (n-1)th term of the progression. This means that the value of any term in the sequence can be easily calculated once we know the common difference and the first term.

Another property is that the sum of the first n terms of an arithmetic progression can be expressed using a formula. The sum is given by the formula $S_n = \frac{n}{2}(2a_1 + (n-1)d)$, where $a_1$ is the first term, $d$ is the common difference, and $n$ is the number of terms.

Arithmetic progressions also have a property related to the arithmetic mean. If a, b, and c are three terms of an arithmetic progression, and b is the arithmetic mean of a and c, then b = (a+c)/2. This property allows us to easily identify whether a sequence of numbers is an arithmetic progression or not.

Finally, arithmetic progressions have other properties such as the fact that they have an infinite number of terms and that the difference between consecutive terms remains constant throughout the sequence.

These properties make arithmetic progressions a powerful tool in mathematics and many other fields. They allow us to easily calculate and analyze sequences of numbers, model real-world phenomena, and solve complex problems.

Applications of Arithmetic Progressions

1. Depreciation of assets: In finance, APs are used to calculate the depreciation of assets over time. The value of an asset decreases by a fixed amount each year, which can be modeled as an AP. The formula for calculating the value of an asset at any given year can be derived using the nth term formula of an AP.

2. Calculation of compound interest: In finance, APs are also used to calculate compound interest, which is the interest earned on an initial investment plus any accumulated interest. The formula for calculating compound interest involves using the sum of an AP formula.

3. Uniform motion: In physics, APs are used to model uniform motion. When an object moves with a constant velocity, its position changes by a fixed amount in a given time interval. This change in position can be modeled as an AP.

4. Time intervals: APs are used to model time intervals in many areas, including computer science, physics, and finance. For example, when measuring the time it takes to perform a task, the time intervals can be modeled as an AP.

5. Searching and sorting algorithms: In computer science, APs are used in various algorithms for searching and sorting data. For example, binary search algorithms work by dividing the search space in half repeatedly until the desired value is found, which can be modeled as an AP.

Frequently Asked Questions