JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Q. A piece of wire is bent in the shape of a parabola y = $\mathrm{Kx}^{2}$ (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is
[IIT-JEE-2009]
(A) $\frac{\mathrm{a}}{\mathrm{gk}}$ (B) $\frac{\mathrm{a}}{2 \mathrm{gk}}$ (C) $\frac{2 \mathrm{a}}{\mathrm{gk}}$ (D) $\frac{\mathrm{a}}{4 \mathrm{gk}}$
Ans. (B)
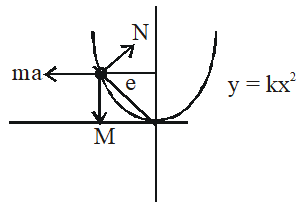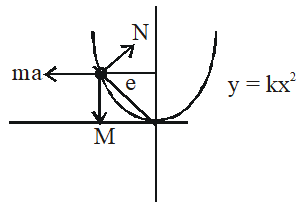$\operatorname{ma} \cos \theta=\operatorname{mg} \sin \theta$
$\mathrm{a}=\mathrm{g} \tan \theta$
$\frac{a}{g}=\tan \theta$
$\frac{a}{g}=2 k x$
$\frac{a}{2 g k}=x$
$\operatorname{ma} \cos \theta=\operatorname{mg} \sin \theta$
$\mathrm{a}=\mathrm{g} \tan \theta$
$\frac{a}{g}=\tan \theta$
$\frac{a}{g}=2 k x$
$\frac{a}{2 g k}=x$
Comments
lollllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllhhhhhhhhhhhhhg
June 25, 2021, 4:10 p.m.
lol 😂