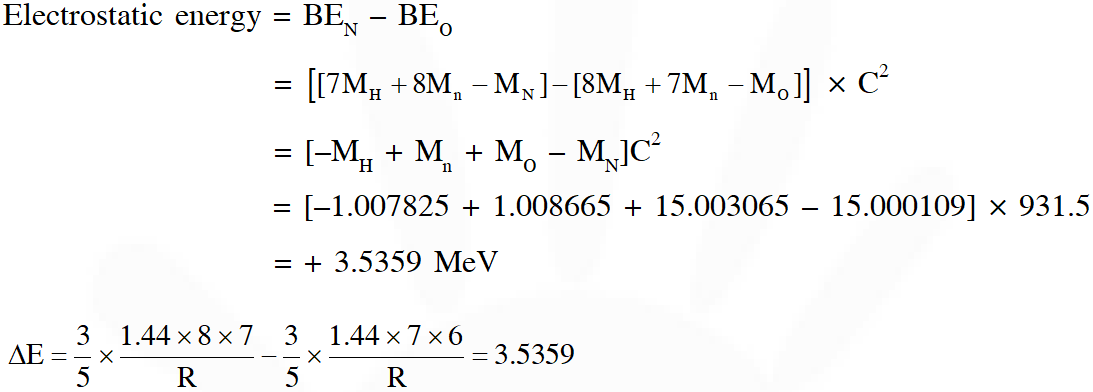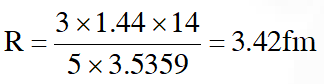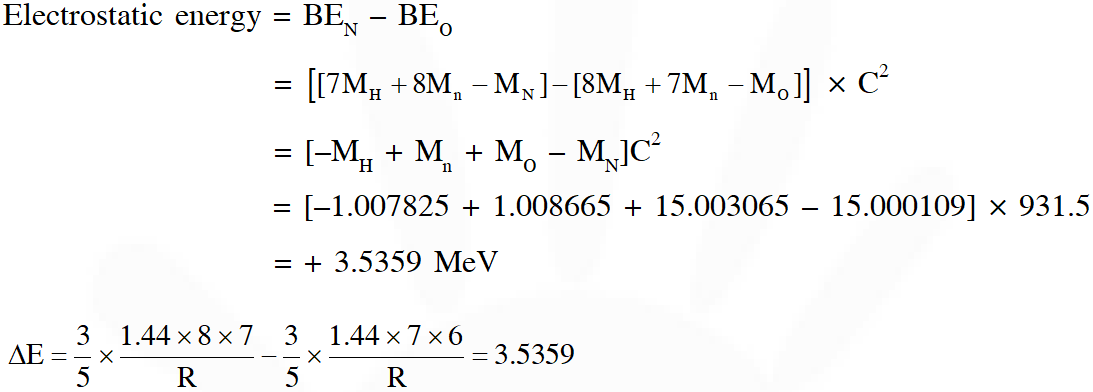JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions.
Paragraph for Question Nos. 1 to 3
Scientists are working hard to develop nuclear fusion reactor. Nuclei of heavy hydrogen, $_{1}^{2} \mathrm{H}$, known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The
D-D reaction is $_{1}^{2} \mathrm{H}+_{1}^{2} \mathrm{H} \rightarrow_{2}^{3} \mathrm{He}+\mathrm{n}+$ energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of $_{1}^{2} \mathrm{H}$ nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma. Special techniques are used which confine the plasma for a time $\mathrm{t}_{0}$ before the particles fly away from the core. If n is the density (number/volume) of deuterons, the product $\mathrm{nt}_{0}$ is called Lawson number. In one of the criteria, a reactor is termed successful if Lawson number is greater than $5 \times 10^{14} \mathrm{s} / \mathrm{cm}^{3}$. It may be helpful to use the following :
Boltzmann constant $\mathrm{k}=8.6 \times 10^{-5} \mathrm{eV} / \mathrm{K} ; \frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}=1.44 \times 10^{-9} \mathrm{eVm}$
Paragraph for Questions 5 and 6
The mass of a nucleus $_{\mathrm{Z}}^{\mathrm{A}} \mathrm{X}$ is less than the sum of the masses of (A – Z) number of neutrons and Z number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ only if $\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right)$ < M. Also two light nuclei of masses $\mathrm{m}_{3}$ and $\mathrm{m}_{4}$ can undergo complete fusion and form a heavy nucleus of mass M' only if $\left(\mathrm{m}_{3}+\mathrm{m}_{4}\right)$ > M'. The masses of some neutral atoms are given in the table below :-
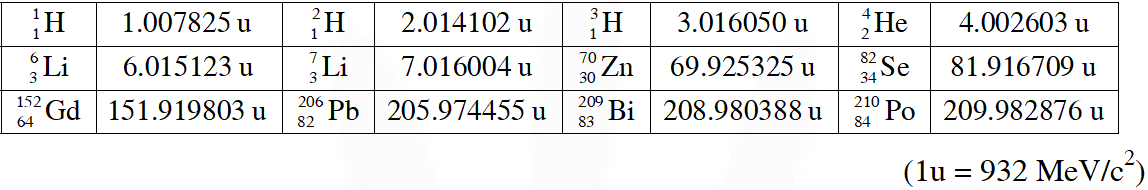
Q. In the core of nuclear fusion reactor, the gas becomes plasma because of -
(A) strong nuclear force acting between the deuterons
(B) Coulomb force acting between the deuterons
(C) Coulomb force acting between deuteron-electron pairs
(D) the high temperature maintained inside the reactor core
[JEE-2009]
Ans. (D)
Due to the high temperature developed as a result of collision & fusion causes the core of fusion reactor to plasma.
Q. Assume that two deuteron nuclei in the core of fusion reactor at temperature T are moving towards each other, each with kinetic energy 1.5 kT, when the separation between them is large enough to neglect Coulomb potential energy. Also neglect any interaction from other particles in the core. The minimum temperature T required for them to reach a separation of 4 × $10^{-15}$ m is in the range
(A) $1.0 \times 10^{9} \mathrm{K}<\mathrm{T}<2.0 \times 10^{9} \mathrm{K}$
(B) $2.0 \times 10^{9} \mathrm{K}<\mathrm{T}<3.0 \times 10^{9} \mathrm{K}$
(C) $3.0 \times 10^{9} \mathrm{K}<\mathrm{T}<4.0 \times 10^{9} \mathrm{K}$
(D) $4.0 \times 10^{9} \mathrm{K}<\mathrm{T}<5.0 \times 10^{9} \mathrm{K}$
[JEE-2009]
Ans. (A) $\left(\frac{3}{2} \mathrm{KT}\right) 2=\frac{\mathrm{Kq}_{1} \mathrm{q}_{2}}{\mathrm{r}} 3 \mathrm{KT}=\frac{\mathrm{Kq}_{1} \mathrm{q}_{2}}{\mathrm{r}}$
$\mathrm{T}=\frac{1.44 \times 10^{-9}}{4 \times 10^{-15} \times 3 \times 8.6 \times 10^{-5}}$
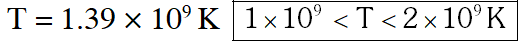
Q. Results of calculations for four different designs of a fusion reactor using D-D reaction are given below. Which of these is most promising based on Lawson criterion?
(A) deuteron density $=2.0 \times 10^{12} \mathrm{cm}^{-3},$ confinement
time $=5.0 \times 10^{-3} \mathrm{s}$
(B) deuteron density $=8.0 \times 10^{14} \mathrm{cm}^{-3},$ confinement time $=9.0 \times 10^{-1} \mathrm{s}$
(C) deuteron density $=4.0 \times 10^{23} \mathrm{cm}^{-3},$ confinement time $=1.0 \times 10^{-11} \mathrm{s}$
(D) deuteron density $=1.0 \times 10^{24} \mathrm{cm}^{-3},$ confinement time $=4.0 \mathrm{x} 10^{-12} \mathrm{s}$
[JEE-2009]
Ans. (B)
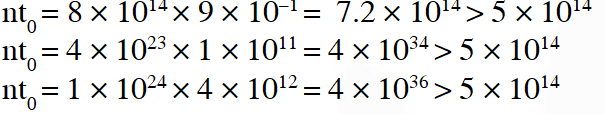
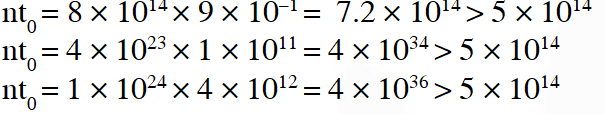
Q. What is the maximum energy of the anti-neutrino?
(A) zero
(B) much less than $0.8 \times 10^{6} \mathrm{eV}$
(C) Nearly $0.8 \times 10^{6} \mathrm{eV}$
(D) Much larger than $0.8 \times 10^{6} \mathrm{eV}$
[JEE 2012]
Ans. (C)
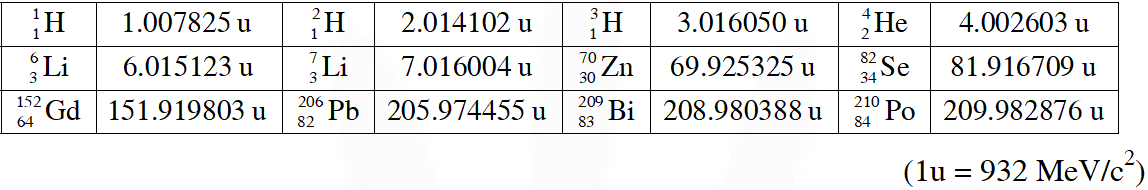
Q. The kinetic energy (in keV) of the alpha particle, when the nucleus 210
84 $P O$ at rest undergoes alpha decay, is :-
(A) 5319 (B) 5422 (C) 5707 (D) 5818
[JEE Advance-2013]
Ans. (A)
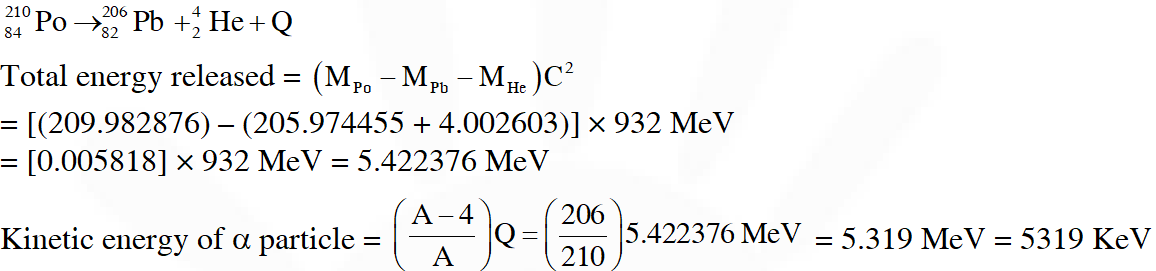
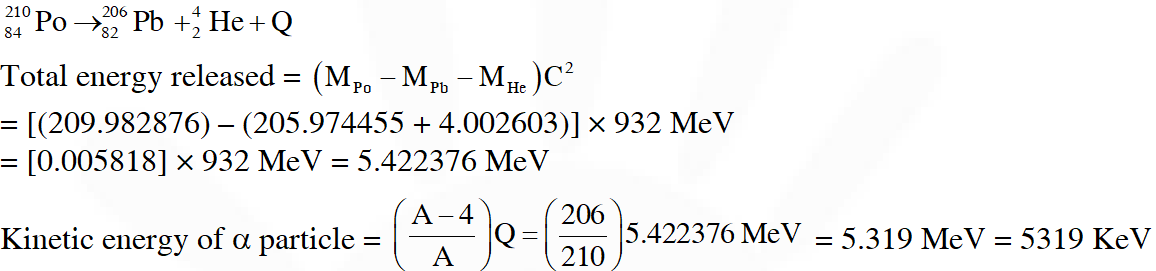
Q. The correct statement is :-
(A) The nucleus $_{3}^{6}$ Li can emit an alpha particle
(B) The nucleus $_{84}^{210}$ Po can emit a proton
(C) Deuteron and alpha particle can undergo complete fusion
(D) The nuclei $_{30}^{70} \mathrm{Zn}$ and $_{34}^{82} \mathrm{Se}$ can undergo complete fusion
[JEE Advance-2013]
Ans. (C)
Q. Match List I of the nuclear processes with List II containing parent nucleus and one of the end products of each process and then select the correct answer using the codes given below the lists:
[JEE Advance-2013]
[JEE Advance-2013]
Ans. (C)
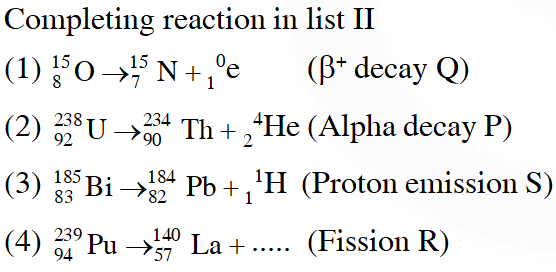
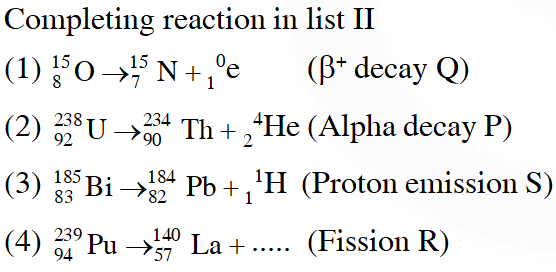
Q. A fission reaction is given by $_{92}^{236} \mathrm{U} \rightarrow_{54}^{140} \mathrm{Xe}+_{38}^{94} \mathrm{Sr}+\mathrm{x}+\mathrm{y},$ where $\mathrm{x}$ and $\mathrm{y}$ are two particles.
Considering $_{92}^{236} \mathrm{U}$ to be at rest, the kinetic energies of the products are denoted by
$\mathrm{K}_{\mathrm{Xe}}, \mathrm{K}_{\mathrm{sr}}, \mathrm{K}_{\mathrm{x}}(2 \mathrm{MeV})$ and $\mathrm{K}_{\mathrm{v}}(2 \mathrm{MeV}),$ respectively. Let the binding energies per nucleon of
[JEE Advance-2015]
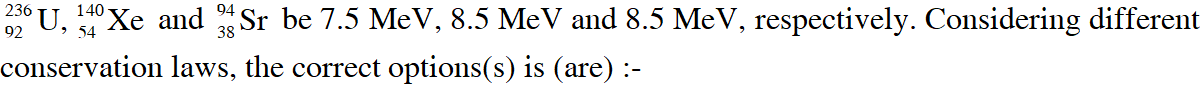[JEE Advance-2015]
Ans. (A)
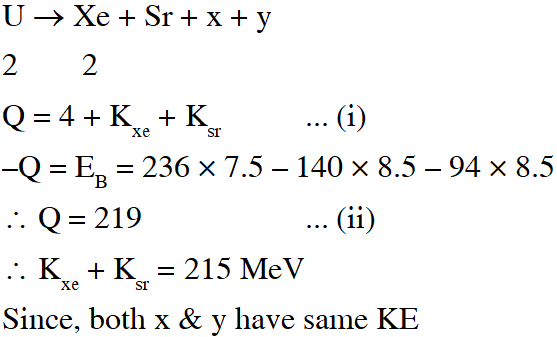
Q. The isotope $_{5}^{12} \mathrm{B}$ having a mass 12.014 u undergoes $\beta$ -decay to $_{6}^{12} \mathrm{C} ._{6}^{12} \mathrm{C}$ has an excited state of
the nucleus $\left(_{6}^{12} \mathrm{C}^{*}\right)$ at $4.041 \mathrm{MeV}$ above its ground state. If 12
5 $\mathrm{decays}$ to $_{6}^{12} \mathrm{C}^{*},$ the maximum
kinetic energy of the $\beta$ -particle in units of MeV is $\left(1 \mathrm{u}=931.5 \mathrm{MeV} / \mathrm{c}^{2}\right.$, where c is the speed of light in vacuum).
[JEE Advance-2016]
Ans. 9
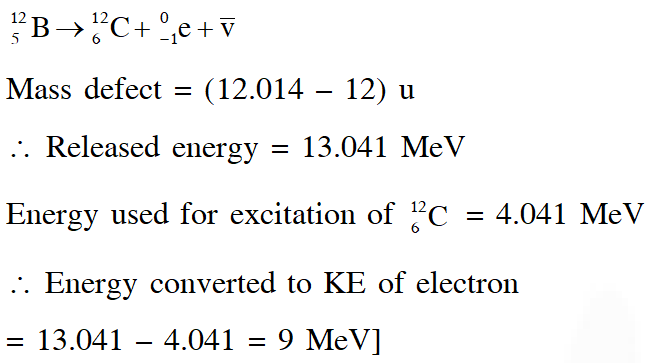
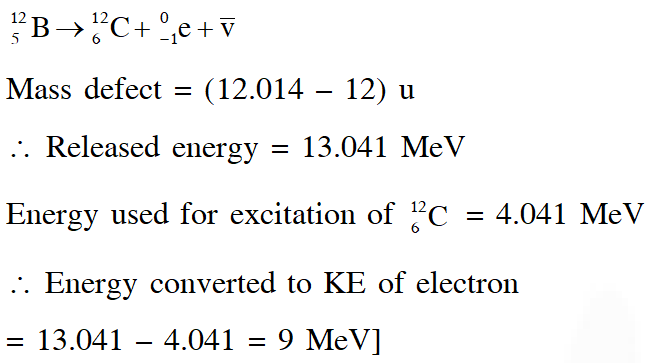
Q. The electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is given by $\mathrm{E}=\frac{3}{5} \frac{\mathrm{Z}(\mathrm{Z}-1) \mathrm{e}^{2}}{4 \pi \varepsilon_{0} \mathrm{R}}$
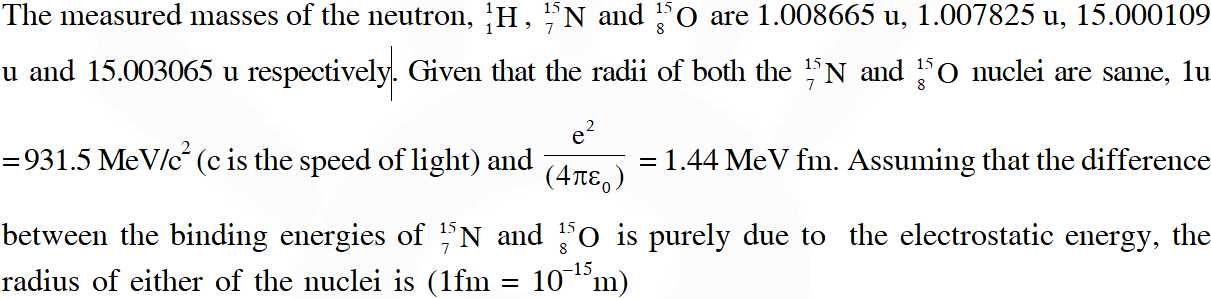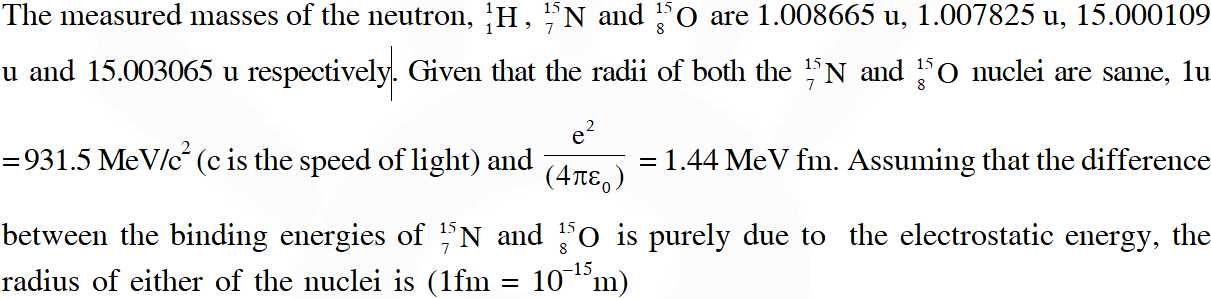(A) 2.85 fm (B) 3.03 fm (C) 3.42 fm (D) 3.80 fm
[JEE Advance-2016]
(A) 2.85 fm (B) 3.03 fm (C) 3.42 fm (D) 3.80 fm
[JEE Advance-2016]
Ans. (C)
