JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1)(1, 1) and (1, 0) is :
(1) $2+\sqrt{2}$
(2) $2-\sqrt{2}$
(3) $1+\sqrt{2}$
(4) $1-\sqrt{2}$
[JEE-MAIN 2013]
Ans. (2)
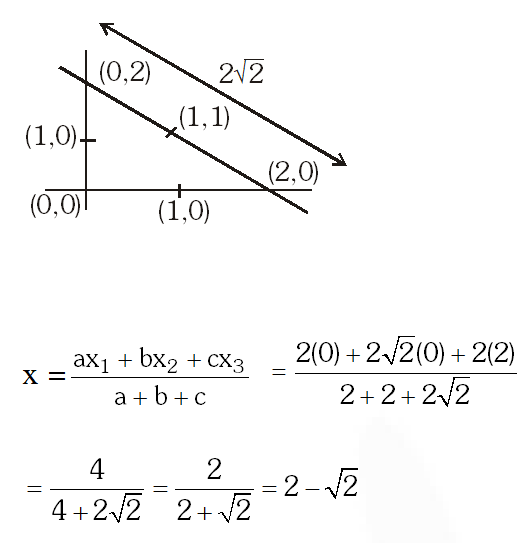
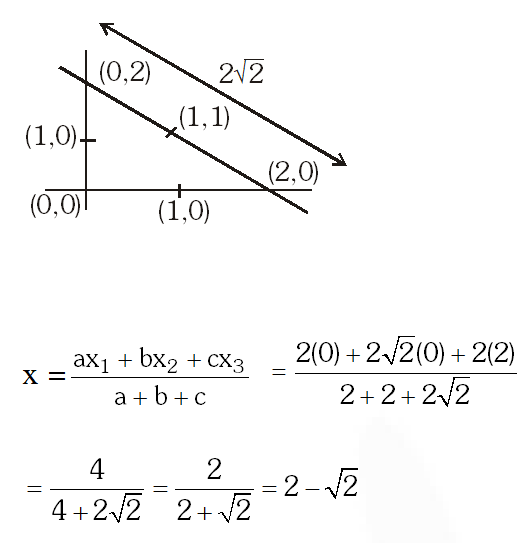
Q. Let $\mathrm{A}(-3,2)$ and $\mathrm{B}(-2,1)$ be the vertices of a triangle ABC. If the centroid of this triangle lies on the line $3 x+4 y+2=0,$ then the vertex $\mathrm{C}$ lies on the line:
(1) 4x + 3y + 5 = 0
(2) 3x + 4y + 5 = 0
(3) 3x + 4y + 3 = 0
(4) 4x + 3y + 3 = 0
[JEE-MAIN Online 2013]
Ans. (3)
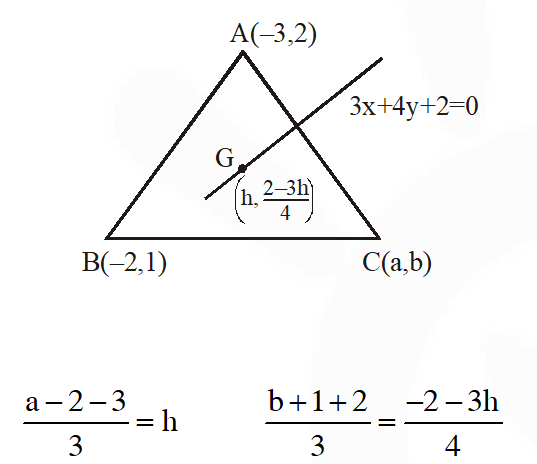
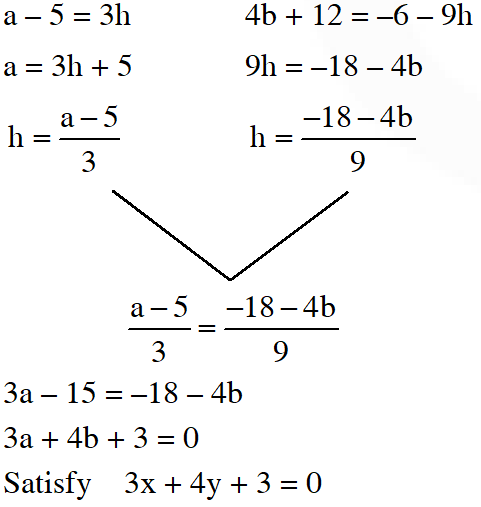
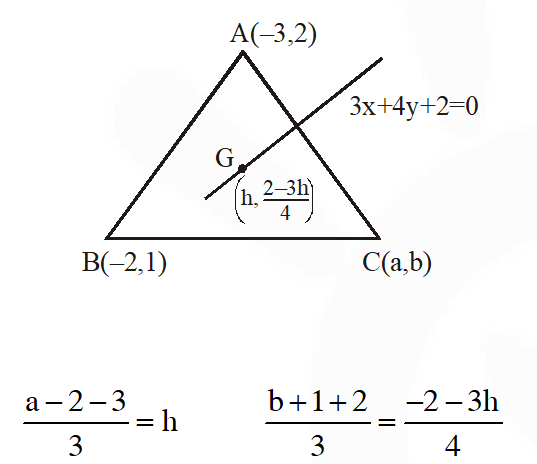
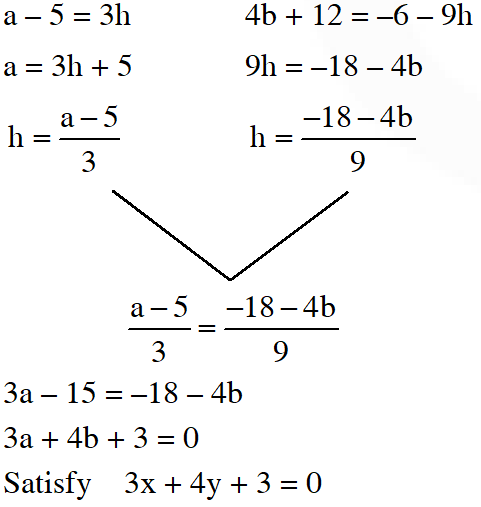
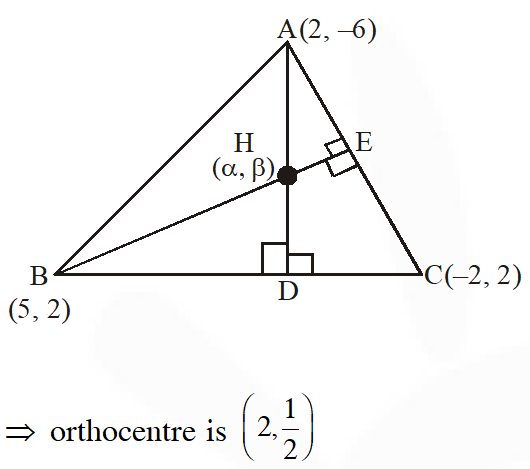
Q. Let k be an integer such that triangle with vertices (k, –3k), (5, k) and (–k, 2) has area 28 sq. units. Then the orthocentre of this triangle is at the point :
(1) $\left(2, \frac{1}{2}\right)$
( 2)$\left(2,-\frac{1}{2}\right)$
(3) $\left(1, \frac{3}{4}\right)$
(4) $\left(1,-\frac{3}{4}\right)$
[JEE(Main)-2017]
Ans. (1)
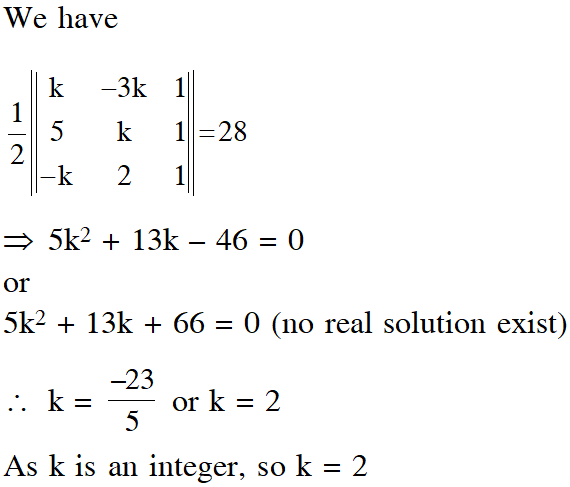
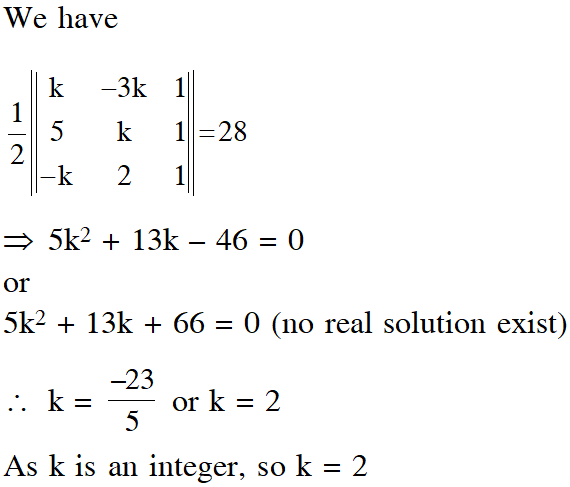

Q. Let the orthocentre and centroid of a triangle be A(–3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter, is:
(1) $2 \sqrt{10}$
(2) $3 \sqrt{\frac{5}{2}}$
(3) $\frac{3 \sqrt{5}}{2}$
(4) $\sqrt{10}$
[JEE(Main)-2018]
Ans. (2)


