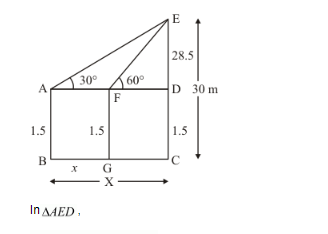
A 1.5 m tall boy is standing at some distance from a 30 m tall building.

Let BG be the distance of tall Boy x and he walks towards the building, makes an angle of elevation at top of building increase from 30° to 60°.

Therefore ∠A = 30° and ∠F = 60° given CE = 30 m, AB = 15 m, FG = 1.5 and DE = 28.5, GC = X − x and FD = X − x

We have to find x

The corresponding figure is as follows

$\Rightarrow \quad \tan A=\frac{E D}{A D}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{28.5}{X}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{28.5}{X}$

$\Rightarrow \quad X=49.36$

Again in $_{\triangle E F D}$,

$\Rightarrow \quad \tan F=\frac{D E}{F D}$

$\Rightarrow \quad \tan 60^{\circ}=\frac{28.5}{X-x}$

$\Rightarrow \quad \sqrt{3}=\frac{28.5}{49.36-x}$

$\Rightarrow \quad 28.5=49.36 \sqrt{3}-\sqrt{3} x$

$\Rightarrow \quad x=\frac{57}{\sqrt{3}}$

$\Rightarrow \quad x=19 \sqrt{3}$

Hence the required distance is $19 \sqrt{3} \mathrm{~m}$.