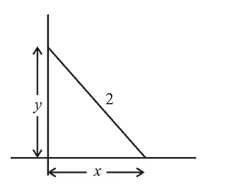
A $2 \mathrm{~m}$ ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate $25 \mathrm{~cm} / \mathrm{sec}$., then the rate (in $\mathrm{cm} / \mathrm{sec}$.) at which the bottom of the ladder slides away from the wall on the horizontal ground when the top of the ladder is $1 \mathrm{~m}$ above the ground is:
Correct Option: , 2
According to the question,
$\frac{d y}{d t}=-25$ at $y=1$
By Pythagoras theorem, $x^{2}+y^{2}=4$ .....(i)
When $y=1 \Rightarrow x=\sqrt{3}$
Diff. equation (i) w. r. $\mathrm{t} . t$
$2 x \frac{d x}{d t}+2 y \frac{d y}{d t}=0$
$\Rightarrow x \frac{d x}{d t}+y \frac{d y}{d t}=0 \Rightarrow \sqrt{3} \frac{d x}{d t}+(-25)=0$
$\Rightarrow \frac{d x}{d t}=\frac{25}{\sqrt{3}} \mathrm{~cm} / \mathrm{s}$
