Question:
A $\triangle A B C$ is given. If lines are drawn through $A, B, C$, parallel respectively to the sides $B C, C A$ and $A B$, forming $\triangle P Q R$, as shown in the adjoining figure, show that $B C=\frac{1}{2} Q R$.
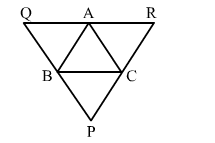
Solution:
BC || QA and CA || QB
i.e., BCQA is a parallelogram.
∴ BC = QA ...(i)
Similarly, BC || AR and AB || CR.
i.e., BCRA is a parallelogram.
∴ BC = AR ...(ii)
But QR = QA + AR
From (i) and (ii), we get:
QR = BC + BC
⇒ QR = 2BC
$\therefore B C=\frac{1}{2} Q R$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.