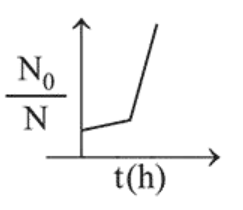
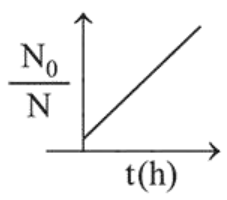
A bacterial infection in an internal wound grows as $\mathrm{N}^{\prime}(\mathrm{t})=$ $\mathrm{N}_{0} \exp (\mathrm{t})$, where the time $\mathrm{t}$ is in hours. A dose of antibiotic, taken orally, needs 1 hour to reach the wound. Once it reaches there, the bacterial population goes down as $\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}=-5 \mathrm{~N}^{2}$. What will be the plot of $\frac{\mathrm{N}_{0}}{\mathrm{~N}} \mathrm{vs}$. t after 1 hour?
Correct Option: , 3
When drug is administered bacterial growth is given by $\frac{d N}{d t}=-5 N^{2}$
On integrating the above equation,
$\Rightarrow \frac{\mathrm{N}_{0}}{\mathrm{~N}_{\mathrm{t}}}=1+5 \mathrm{t} \mathrm{N}_{0}$
The above equation is similar to straight line equation
with positive slope.
Thus $\frac{\mathrm{N}_{0}}{\mathrm{~N}_{\mathrm{t}}}$ increases linearly with $\mathrm{t}$.