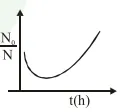
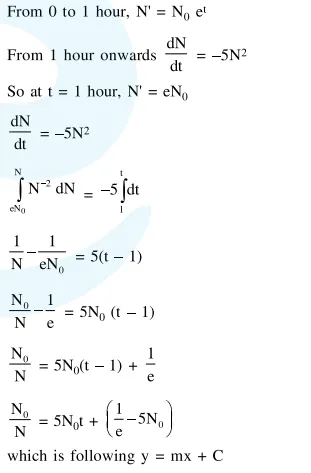Question:
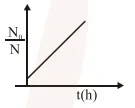
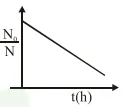
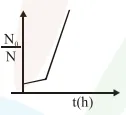
A bacterial infection in an internal wound grows as $N^{\prime}(t)=N_{0} \exp (t)$, where the time $t$ is in hours. A dose of antibiotic, taken orally, needs 1 hour to reach the wound. Once it reaches there, the bacterial population goes down as $\frac{\mathrm{dN}}{\mathrm{dt}}=-5 \mathrm{~N}^{2}$. What will be the plot of $\frac{\mathrm{N}_{0}}{\mathrm{~N}}$ vs. t after 1 hour ?
Correct Option: 1
Solution: