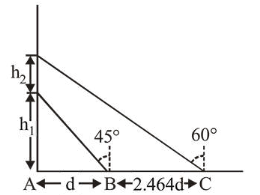
A balloon is moving up in air vertically above a point $\mathrm{A}$ on the ground. When it is at a height $h_{1}$, a girl standing at a distance $d$ (point B) from A (see figure) sees it at an angle $45^{\circ}$ with respect to the vertical. When the balloon climbs up a further height $h_{2}$, it is seen at an angle $60^{\circ}$ with respect to the vertical if the girl moves further by a distance $2.464 d$ (point C). Then the height $h_{2}$ is (given $\tan 30^{\circ}=$ $0.5774)$ :
Correct Option: , 4
(4) From figure/ trigonometry,
$\frac{h_{1}}{d}=\tan 45^{\circ}$' $\therefore h_{1}=d$
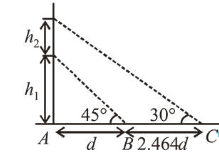
And, $\frac{h_{1}+h_{2}}{d+2.464 d}=\tan 30^{\circ}$
$\Rightarrow\left(h_{1}+h_{2}\right) \times \sqrt{3}=3.46 d$
$\Rightarrow\left(h_{1}+h_{2}\right)=\frac{3.46 d}{\sqrt{3}} \Rightarrow d+h_{2}=\frac{3.46 d}{\sqrt{3}}$
$\therefore h_{2}=d$
