A battery of $3.0 \mathrm{~V}$ is connected to a resistor dissipating $0.5$ W of power. If the termial voltage of the battery is
$2.5 \mathrm{~V}$, the power dissipated within the internal resistance is:
Correct Option: , 3
(3) When resistor is connected power dissipated,
$P_{R}=0.5 \mathrm{~W}$
Emf of battery, $E=3 \mathrm{~V}$ Terminal voltage, $V=2.5 \mathrm{~V}$
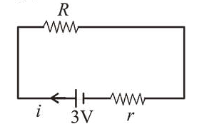
$P_{R}=i^{2} R=0.5 \mathrm{~W}$
Also, $V=E-i r \Rightarrow 2.5=3-i r \Rightarrow i r=0.5$
Power dissipated across $' r^{\prime}: P_{r}=i^{2} r$
Now $i R=2.5$ and $i r=0.5$
$\therefore \frac{R}{r}=5$
Now $\frac{P_{R}}{P_{r}}=\frac{i^{2} R}{i^{2} r} \Rightarrow \frac{P_{R}}{P_{r}}=\frac{R}{r} \Rightarrow \frac{P_{R}}{P_{r}}=5$
$\Rightarrow P_{r}=\frac{P_{R}}{5}=\frac{0.50}{5}$
$\therefore P_{r}=0.10 \mathrm{~W}$
