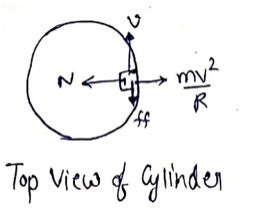
Question:
A block of mass $m$ moves on a horizontal circle against the wall of a cylindrical room of radius $R$. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is $g$. The block is given an initial speed $v_{0}$. As a function of the speed $v$ write (a) the normal force by the wall on the block, (b) the frictional force by the wall and (c) the tangential acceleration of the block. (d) Integrate the tangential acceleration $(d v / d t=v d v / d s)$ to obtain the speed of the block after one revolution.
Solution: