A chord is at a distance of 8 cm from the centre of a circle of radius 17 cm.
Chord Length in a Circle uses the Pythagorean theorem and the property that a perpendicular from the centre bisects a chord to find the chord length as 30 cm.
A chord is at a distance of 8 cm from the centre of a circle of radius 17 cm. The length of the chord is
(a) 25 cm
(b) 12.5 cm
(c) 30 cm
(d) 9 cm
(c) 30 cm
Let AB be the chord of the given circle with centre O and a radius of 17 cm.
From O, draw OM perpendicular to AB.
Then OM = 8 cm and OB = 17 cm
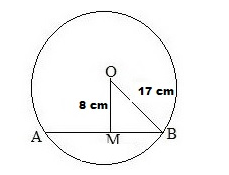
From the right ΔOMB, we have:
$\mathrm{OB}^{2}=\mathrm{OM}^{2}+\mathrm{MB}^{2}$
$\Rightarrow 17^{2}=8^{2}+\mathrm{MB}^{2}$
$\Rightarrow 289=64+\mathrm{MB}^{2}$
$\Rightarrow \mathrm{MB}^{2}=(289-64)=225$
$\Rightarrow \mathrm{MB}=\sqrt{225} \mathrm{~cm}=15 \mathrm{~cm}$
The perpendicular from the centre of a circle to a chord bisects the chord.
∴ AB = 2 × MB = (2 x 15) cm = 30 cm
Hence, the required length of the chord is 30 cm.
Frequently Asked Questions
Find answers to common questions.
What is the length of a chord at a distance of 8 cm from the centre of a circle of radius 17 cm?
The length of the chord is 30 cm. Using the perpendicular from the centre to the chord, a right triangle is formed with hypotenuse 17 cm (radius) and one leg 8 cm (distance). By the Pythagorean theorem, half the chord = √(289 − 64) = 15 cm, so the full chord = 2 × 15 = 30 cm.
What formula is used to find the length of a chord?
The formula is Chord Length = 2√(r² − d²), where r is the radius and d is the perpendicular distance from the centre to the chord. This formula is derived directly from the Pythagorean theorem applied to the right triangle formed by the radius, the perpendicular, and half the chord.
Why does the perpendicular from the centre bisect the chord?
The perpendicular from the centre bisects the chord because of the symmetry of a circle. Any point on a circle is equidistant from the centre, so the two halves of the chord are mirror images across the perpendicular line. This is formally proved using congruent triangles (RHS congruence) in NCERT Class 9, Chapter 10.
What is a Pythagorean triplet and why is 8-15-17 one of them?
Pythagorean triplet is a set of three positive integers (a, b, c) satisfying a² + b² = c². For 8-15-17: 8² + 15² = 64 + 225 = 289 = 17². These triplets appear frequently in geometry problems and instantly tell you the missing side without computing square roots — a major time-saver in MCQ exams.
What happens to the chord length as it moves farther from the centre?
As the chord moves farther from the centre (as d increases), the chord length decreases. When d = 0, the chord is a diameter — the longest possible chord. When d equals the radius, the chord length becomes zero, meaning the line is tangent to the circle and touches it at exactly one point.