A circular disc of mass $M$ and radius $R$ is rotating about its axis with angular speed $\omega_{1}$. If another stationary disc
having radius $\frac{R}{2}$ and same mass $M$ is dropped co-axially
on to the rotating disc. Gradually both discs attain constant angular speed $\omega_{2}$. The energy lost in the process is $p \%$ of the initial energy. Value of $p$ is__________
(20)
As we know moment of inertia disc, $I_{\mathrm{disc}}=\frac{1}{2} M R^{2}$
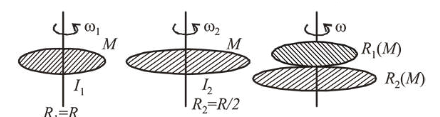
Using angular momentum conservation
$I_{1} \omega_{1}+I_{2} \omega_{2}=\left(I_{1}+I_{2}\right) \times \omega_{f}$
$\frac{M R^{2}}{2} \times \omega+0=\left(\frac{M R^{2}}{2}+\frac{M R^{2}}{8}\right) \omega_{f} \Rightarrow \omega_{f}=\frac{4}{5} \omega$
Initial K.E., $K_{i}=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(\frac{M R^{2}}{2}\right) \omega^{2}=\frac{M R^{2} \omega^{2}}{4}$
Final K.E., $K_{f}=\frac{1}{2}\left(\frac{M R^{2}}{2}+\frac{M R^{2}}{8}\right) \frac{16}{25} \omega^{2}=\frac{M R^{2} \omega^{2}}{5}$
Percentage loss in kinetic energy $\%$ loss
$=\frac{\frac{M R^{2} \omega^{2}}{4}-\frac{M R^{2} \omega^{2}}{5}}{\frac{M R^{2} \omega^{2}}{4}} \times 100=20 \%=P \%$
Hence, value of $P=20$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.