A circus tent is cylindrical to a height of 4 m

Solution:

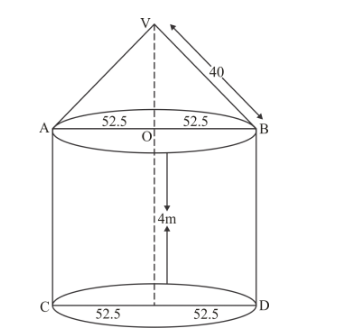
For conical portion

$r=52.5 \mathrm{~m}$ and $l=40 \mathrm{~m}$

Curved surface area of the conical portion

$=\pi r l$

$=\pi \times 52.5 \times 40$

$=2100 \pi \mathrm{m}^{2}$

For cylindrical portion we have

$r=52.5 \mathrm{~m}$ and $h=4 \mathrm{~m}$

Then,

Curved surface area of cylindrical portion

$=2 \pi r h$

$=2 \times \pi \times 52.5 \times 4$

 

$=420 \pi \mathrm{m}^{2}$

Area of canvas used for making the tent

$=(2100 m+420) \pi$

$=2520 \times \frac{22}{7}$

$=7920 \mathrm{~m}^{2}$

Hence, the correct answer is choice (d).